Р.199 СибАДИ
Часть задач есть решенные, контакты
Пример 1
Нефть весом 90 кгс занимает объём 105 см3. Определить плотность и удельный вес этой нефти в трёх системах единиц (СИ, МКГСС, СГС).
Стоимость: 90 руб
Пример 2
Трубопровод диаметром d = 250 мм и длиной L = 1 км заполнили водой при атмосферном давлении. Определить, какой объём воды необходимо добавить в трубопровод, чтобы давление в нём повысилось до 70 ат? Деформацией стенок трубопровода пренебречь.
Стоимость: 90 руб
Пример 3
При температуре 288 К плотность нефти равна 828 кг/м3. При температуре 295 К условная вязкость нефти равна 6,4 ˚Е. Коэффициент температурного расширения нефти βt = 0,00072 1/ К. Определить динамическую вязкость нефти при температуре 295 К.
Стоимость: 90 руб
Задача 1.3.1
Определить плотность нефти, если 320 000 кг её массы помещаются в объёме 380 м3.
Задача 1.3.2
Определить объём, занимаемый 125 000 кг нефти, если её плотность равна 850 кг/м3.
Задача 1.3.3
Определить удельный вес и плотность жидкости, если её объём W = 104 см3 имеет вес G = 8,3 кгс. Решение привести в трёх системах единиц: международной – СИ, технической – МКГСС, физической – СГС.
Задача 1.3.4
Определить потребное число бочек для транспортировки трансформаторного масла весом 117 кН и плотностью 900 кг/м3, если объём одной бочки Wб = 1,2 м3.
Задача 1.3.5
Определить плотность битума, если 470 кН его занимают объём W = 50 м3.
Задача 1.3.6
При гидравлическом испытании трубопровода длиной 600 м и диаметром 500 мм давление воды поднято от 1 ат до 50 ат. Какой объём воды потребовалось подать в трубопровод за время подъёма давления? Расширением стенок трубы пренебречь.
Задача 1.3.7
Сосуд, объём которого 2,0 м3, заполнен водой. На сколько уменьшится и чему станет равным объём воды при увеличении давления на 20 000 кПа? Модуль объёмной упругости воды принять равным 1962∙106 Па.
Задача 1.3.8
При испытании прочности резервуара гидравлическим способом он был заполнен водой при давлении 50∙105 Па. В результате утечки части воды через неплотности давление в резервуаре понизилось до 11,5∙105 Па. Пренебрегая деформацией стенок резервуара, определить объём воды, вытекшей за время испытания. Объём резервуара равен 20 м3.
Стоимость: 100 руб
Задача 1.3.9
Кинематическая вязкость воды при температуре 15˚С равна 0,0115 Ст. Определить динамическую вязкость жидкости в международной, технической и физической системах единиц.
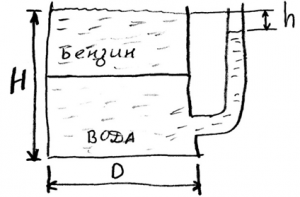
Задача 1.3.10
Удельный вес бензина 720 кгс/м3. Определить плотность этого бензина в международной, технической и физической системах единиц.
Задача 1.3.11
Определить удельный вес и плотность жидкости, если её вес 90 кгс и объём 105 см3. Решение дать в международной, технической и физической системах единиц.
Стоимость: 120 руб
Задача 1.3.12
Плотность нефти 0,86 г/см3. Определить плотность и удельный вес этой нефти в международной и технической системах единиц.
Стоимость: 100 руб
Задача 1.3.13
Удельный вес бензина 7000 Н/м3. Определить плотность и удельный вес этого бензина в международной, технической и физической системах единиц.
Задача 1.3.14
В резервуар, содержащий 125 м3 нефти плотностью 760 кг/м3, закачано 224 м3 нефти плотностью 848 кг/м3. Определить плотность смеси в международной, технической и физической системах единиц.
Стоимость: 100 руб
Задача 1.3.15
В резервуар залито 15 м3 жидкости плотностью 800 кг/м3. Сколько необходимо долить такой же жидкости (однородной), но плотностью 824 кг/м3, чтобы в резервуаре образовалась смесь плотностью 814 кг/м3?
Задача 1.3.16
Стальной толстостенный баллон, объём которого 36 дм3, заполнен нефтью и плотно закрыт при атмосферном давлении. Какое количество нефти необходимо закачать в баллон дополнительно, чтобы давление в нём повысилось в 25 раз? Модуль объёмной упругости нефти равен 1325∙106 Па. Деформацией стенок баллона пренебречь.
Задача 1.3.17
Сосуд ёмкостью 32 л заполнен жидкостью при атмосферном давлении. Вычислить объём жидкости, который необходимо закачать в сосуд для того, чтобы избыточное давление в нём было равно 10 атм. Деформациями стенок сосуда пренебречь. Модуль объёмной упругости для жидкости принять равным 13 500 кгс/см2.
Стоимость: 100 руб
Задача 1.3.18
Один кубический метр нефти имеет массу 0,92 т. Вычислить удельный вес и плотность нефти в физической и технической системах единиц.
Задача 1.3.19
В резервуар залито 20 000 л нефти плотностью 850 кг/м3 и 25∙103 л плотностью 840 кг/м3. Определить плотность смеси.
Стоимость: 120 руб
Задача 1.3.20
В резервуар залито 27 400 л нефти с удельным весом 840 кгс/м3 и 18 900 л нефти с неизвестным удельным весом. Полученная смесь имеет удельный вес 860,4 кгс/м3. Вычислить неизвестный удельный вес.
Задача 1.3.21
Определить кинематическую и динамическую вязкость при плотности жидкости 0,9 г/см3. Показания вискозиметра по Энглеру 40°.
Задача 1.3.22
Кинематическая вязкость нефти 0,4 Ст, а удельный вес равен 9000 Н/м3. Определить динамическую вязкость нефти в международной, технической и физической системах единиц.
Задача 1.3.23
Вязкость нефти, определённая при помощи прибора Энглера, равна 8,5˚E. Определить динамическую вязкость в технической системе единиц, если удельный вес нефти составляет 8 500 Н/м3.
Задача 1.3.24
Резервуар диаметром 700 мм и высотой 1,2 м имеет массу 10 кг. Определить вес резервуара, заполненного водой при температуре 4˚С. Ответ дать в международной системе единиц.
Задача 1.3.25
Вязкость цилиндрового масла 50˚E, удельный вес 900 кгс/м3. Определить динамическую и кинематическую вязкость цилиндрового масла в международной, технической и физической системах единиц.
Задача 1.3.26
При 20˚С кинематическая вязкость глицерина 8,7 Ст, удельный вес 1260 кгс/м3. Вычислить при этой температуре динамическую вязкость глицерина в технической и физической системах единиц.
Задача 1.3.27
Кинематическая вязкость воды при температуре 15˚С равна 0,0115 Ст. Определить динамическую вязкость воды в физической и технической системах единиц. Как изменится вязкость воды при подогреве её до 60˚С.
Задача 1.3.28
При температуре 500˚C и атмосферном давлении водяной пар имеет плотность 0,028 кгс∙с2/м4. Вычислить его удельный объём при этой температуре.
Задача 1.3.29
Сколько будет весить ёмкость объёмом 200 л, если её заполнить водой плотностью 1000 кг/м3? Собственный вес ёмкости 10 кгс. Ответ дать в международной системе единиц.
Задача 1.3.30
Динамическая вязкость воздуха при температуре 0˚С равна 17,0∙10-6 Па∙с. Определить кинематическую вязкость воздуха в системе единиц СГС, если удельный вес равен 12,3 Н/м3.
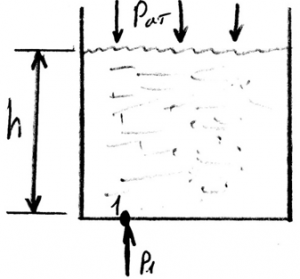
Пример 1
Определить абсолютное давление на дне открытого котлована, наполненного водой до отметки 1,2 м. Результат дать в технических атмосферах (ат).
Стоимость: 90 руб
Пример 2
Нижняя часть рабочей камеры кессона находится на глубине h = 30,0 м от свободной поверхности воды. Определить избыточное давление воздуха p, которое необходимо создать в рабочей камере кессона, чтобы вода из реки не могла проникнуть в камеру.
Стоимость: 90 руб
Пример 3
Найти давление на свободной поверхности воды p0 в замкнутом резервуаре, если уровень жидкости в открытом пьезометре (рис.4) выше уровня жидкости в резервуаре на h = 2,0 м.
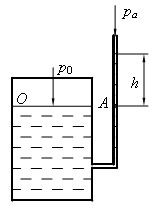
Стоимость: 90 руб
Пример 4
В U-образный сосуд налиты ртуть и вода (рис. 5). Линия раздела жидкостей N – N расположена ниже свободной поверхности ртути на величину hðò = 8 см. Определить разность уровней h в обеих частях сосуда.
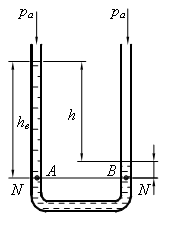
Стоимость: 90 руб
Пример 5
Канал с водой прямоугольного сечения шириной В = 3,5 м перегорожен подъёмным щитом (рис. 6), который помещается в параллелях (пазах) боковых сторон канала. Определить равнодействующую силу гидростатического давления на щит P и подъёмное усилие R, если коэффициент трения щита о параллели f = 0,35; вес щита G = 250 кгс; уровень воды слева от щита h1 = 4,0 м; уровень воды справа от щита h2 = 1,2 м.
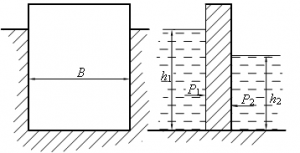
Стоимость: 210 руб
Пример 6
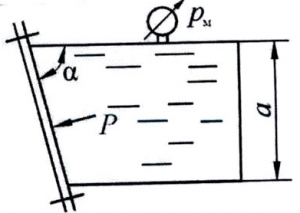
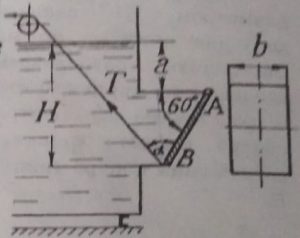
Найти величину и направление силы гидростатического давления на 1,0 погонный метр ширины b секторного затвора (рис. 7) радиусом R = 2,5 м, если угол α = 60˚.
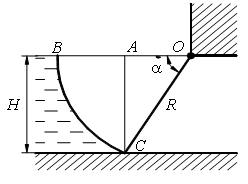
Стоимость: 210 руб
Пример 7
Бетонная плита весит в воздухе G = 1 230 Н, а в воде её вес меньше и составляет Gв = 735 Н. Определить удельный вес этого бетона.
Стоимость: 120 руб
Задача 2.3.1
Определить величину абсолютного давления на поверхности резервуара, если уровень жидкости в пьезометре превышает уровень свободной поверхности в резервуаре на 4,3 м. Плотность жидкости равна 930 кг/м3.
Задача 2.3.2
Определить абсолютное, избыточное, вакуумметрическое давление в точках 1, 2, 3, 4
заполненной водой ёмкости (рис. 8) и опущенных в неё закрытых сверху герметичных вертикальных трубках, если известно, что h1 = h3= 0; h2 = 2,0 м; h4 = 5,0 м. Ускорение свободного падения принять равным 10 м/с2.
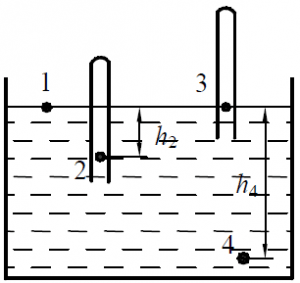
Задача 2.3.3
Как отличаются силы гидростатического давления и координаты погружения центров давления на квадратный и прямоугольный затворы с одинаковым погружением их центров тяжести и одинаковой площадью, если основание прямоугольного затвора меньше его высоты.
Задача 2.3.4
U-образный ртутный манометр подключён к резервуару, заполненному водой (рис. 9). Подсчитать:
а) давление на поверхности воды в резервуаре p0, если h1 = 150 мм, h2 = 250 мм, pа = 100 кПа;
б) высоту ртутного столба h2, если p0 = pа и h1 = 252 мм.
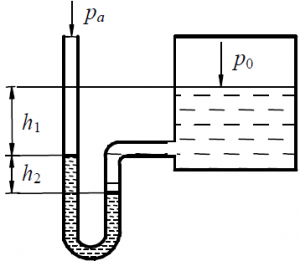
Задача 2.3.5
Каково показание U-образного ртутного манометра (см. рис. 9), подключённого к резервуару с водой, если:
а) h1 + h2 = 400 мм; p0 = 107,87 кПа; pа =98 070 Па;
б) h1 + h2 = 500 мм; p0 = 122 580 Па; pа =101 000 Па.
Задача 2.3.6
Сообщающиеся сосуды заполнены различными жидкостями (рис. 10). Удельный вес одной жидкости γ1 = 7 350 Н/м3, удельный вес другой – γ2 = 12 260 Н/м3, давление
на свободной поверхности в сосудах p1 = p2 = pа. Вычислить:
а) расстояние от линии раздела AB до уровня жидкости в каждом сосуде h1 и h2 при разности уровней жидкостей в сосудах h = 10 см;
б) разность уровней h при h1 = 40 см.
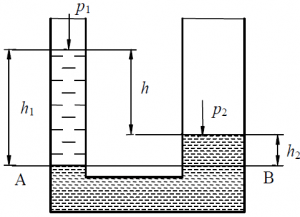
Задача 2.3.7
Вычислить избыточное давление на забое скважины глубиной 1200 м, заполненной глинистым раствором удельного веса γ = 1200 кгс/м3.
Задача 2.3.8
На сколько снизится давление на забое скважины глубиной 3200 м, если глинистый раствор плотностью ρ = 1600 кг/м3 заменить водой?
Задача 2.3.9
Вычислить избыточное гидростатическое давление на забое скважины, в которой имеется столб воды высотой 94 м, а поверх него столб нефти высотой 46 м. Плотность нефти принять равной 872 кг/м3.
Задача 2.3.10
Длинная трубка, имеющая внутренний диаметр 100 мм и открытая по концам, погружена в вертикальном положении в резервуар с водой (рис. 11).В верхний конец трубки залито 8 кг масла, плотность которого ρ = 0,88 г/см3.
На какой высоте h над уровнем воды в резервуаре установится уровень масла в трубке?
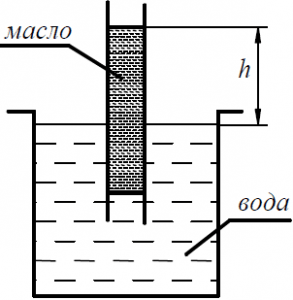
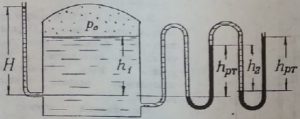
Задача 2.3.11
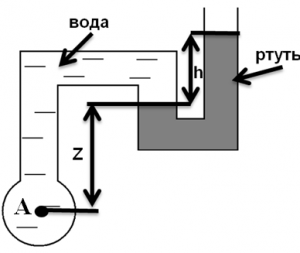
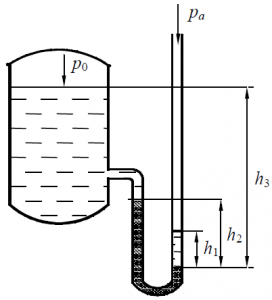
В закрытом сосуде (рис. 12) находится вода. Давление в сосуде p0. В открытом конце манометрической трубки над ртутью имеется столб воды высотой h1 = 15 см. Разность высот h2 = 23 см, h3 = 35 см. Вычислить абсолютное давление в сосуде.
Стоимость: 120 руб
Задача 2.3.12
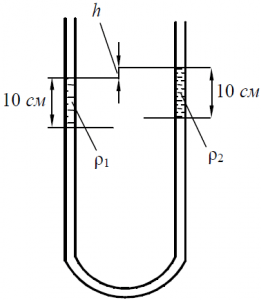
В U-образную трубку налиты две равные по объёму жидкости: вода плотностью ρ1 = 1000 кг/м3 и керосин плотностью ρ2 = 800 кг/м3. Высота столба каждой жидкости составляет 10 см (рис. 13). Определить разность уровней h.
Стоимость: 120 руб
Задача 2.3.13
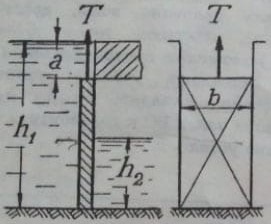
Два сосуда А и В (рис. 14) одинакового диаметра D = 2,0 м заполнены водой. Сосуд А открыт. Сосуд В плотно закрыт крышкой, в небольшое отверстие которой вставлена тонкая трубка. Определить силу гидростатического давления на дно каждого сосуда, если:
а) HА = 2,0 м; HВ = 10,0 м; h = 1,0 м;
б) HА = 3,0 м; HВ = 3,0 м; h = 1,0 м.

Задача 2.3.14
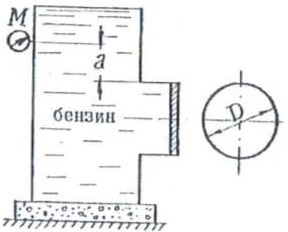
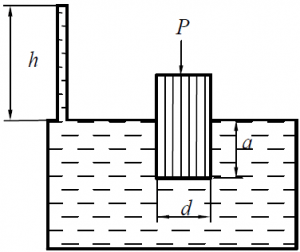
Какую силу необходимо приложить к плунжеру, диаметр которого d = 200 мм, чтобы при его погружении в воду на глубину а = 300 мм уровень воды в пьезометрической трубке был равным h = 1,2 м (рис. 15)? Собственный вес плунжера не учитывать.
Задача 2.3.15
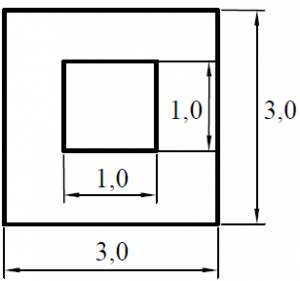
Определить силу давления воды на дно сосуда и на каждую из четырёх опор. Размеры сосуда указаны на чертеже (рис.16).
Задача 2.3.16
Найти силу давления воды на круглый щит, перекрывающий отверстие в вертикальной стенке (рис. 17) и точку приложения равнодействующей hД. Диаметр щита D =1,0 м, уровень воды над щитом h = 3,0 м.

Задача 2.3.17
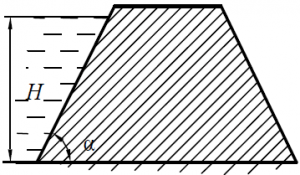
Найти величину силы, сдвигающей насыпь (рис. 18), если глубина воды H = 6,0 м, α = 60˚. Расчёт выполнить на 1,0 погонный метр длины насыпи b.
Стоимость: 180 руб
Задача 2.3.18
Какую силу P2 нужно приложить к большему поршню, чтобы система находилась в равновесии, если P1 = 150 Н, D = 300 мм, h = 80 см, d = 20 мм (рис. 19)?

Задача 2.3.19
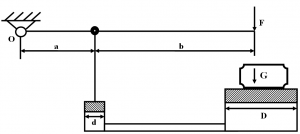
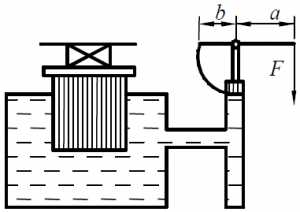
Гидравлический домкрат (рис. 20) имеет диаметр большего поршня D = 250 мм, а диаметр меньшего поршня d = 25 мм; коэффициент полезного действия η = 0,8. Плечи рычага a = 1,0 м и b = 0,2 м. Определить:
а) усилие F, которое необходимо приложить на конце рычага, чтобы поднять груз G =20 кН;
б) максимальную грузоподъёмность домкрата G из условия, что усилие F не будет превышать 10 кгс.
Задача 2.3.20
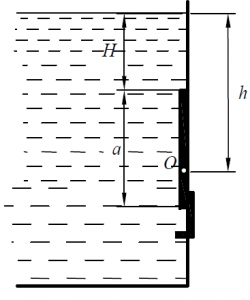
Для регулирования уровня воды в напорном баке установлен поворачивающийся щиток, который должен открывать квадратное отверстие с размером а = 0,4 м в вертикальной стенке (рис. 21) при напоре H = 2,0 м. Найти глубину погружения h шарнира О и силу давления на щиток.
Задача 2.3.21
Чему равно полное давление в трубе в единицах СИ, если манометр показывает давление 2,0 кгс/см2?
Задача 2.3.22
Манометр, установленный на водопроводной трубе, показывает давление 1,5 кгс/см2. Какой пьезометрической высоте соответствует это давление?
Задача 2.3.23
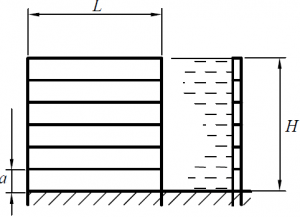
Вертикальный щит, составленный из шести досок длиной L = 2,0 м, одинаковой ширины, а = 25 см, сдерживает столб воды высотой H = 1,0 м (рис. 22). Вычислить силу гидростатического давления на щит и на каждую доску в отдельности.
Стоимость: 180 руб
Задача 2.3.24
Сила давления воды через обшивку прямоугольного щита высотой H = 4,0 м и шириной B = 6,0 м передаётся на четыре горизонтальные балки (рис. 23). На каких расстояниях x от свободной поверхности следует их расположить, чтобы они были нагружены одинаково?

Стоимость: 210 руб
Задача 2.3.25
Плоская боковая стенка резервуара собрана из вертикальных досок шириной а = 12 см. Каждая из досок закреплена двумя болтами, расстояние между которыми L = 110 см (рис. 24). Расстояние от дна резервуара до нижнего болта b = 5 см. Резервуар заполнен водой до уровня h = 75 см. Вычислить усилия, растягивающие верхний и нижний болты.
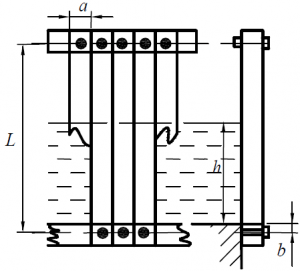
Задача 2.3.26
Вычислить силу гидростатического давления на щит, перекрывающий треугольный водослив размерами: h = 0,9 м и b = 0,8 м (рис. 25).
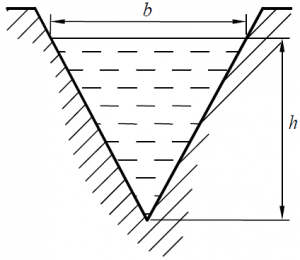
Задача 2.3.27
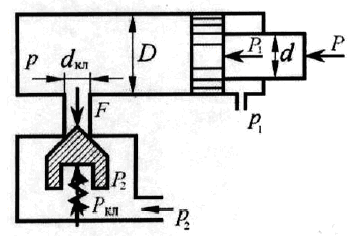
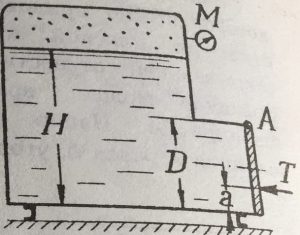
Открытый резервуар снабжён грузовым клапаном, предохраняющим резервуар от поднятия жидкости выше определённого уровня (рис. 26). Размеры клапана: d = 60 мм, a = 120 мм, b = 340 мм. Подобрать вес груза G с таким расчётом, чтобы клапан открывался при поднятии уровня жидкости в резервуаре до высоты H = 2,4 м. Удельный вес жидкости принять γ = 9,2 кН/м3. Собственным весом клапана, тяги к нему и рычага пренебречь.

Стоимость: 150 руб
Задача 2.3.28
Определить натяжение троса, удерживающего прямоугольный щит шириной b = 2,0 м при глубине воды перед щитом H = 1,8 м (рис. 27), если угол наклона щита: а) α = 60˚; б) α = 45˚.
Указание: весом щита пренебречь.
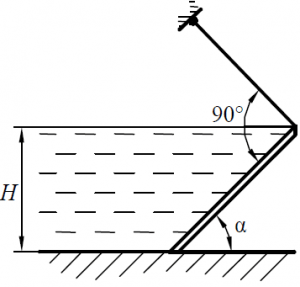
Задача 2.3.29
Прямоугольный щит длиной a = 5,0 м и шириной b = 5,0 м закреплён шарнирно в точке О (рис.28). Уровень воды слева H1 = 4,0 м, справа H2 = 2,0 м. Щит упирается в дно под углом α = 60˚. Определить:
а) реакции опор А и О;
б) усилие T, необходимое для подъёма щита.

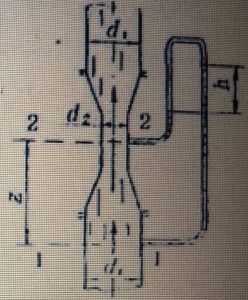
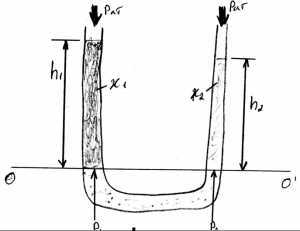
Задача 2.3.30
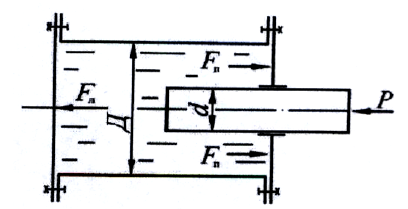
Неподвижный сосуд , с оставленный из двух цилиндров, заполнен жид костью, удерживаемой поршнями, на которые действуют соответствующие силы P1 и P2. Система находится в равновесии. Определить усилие P2, если P1 = 100 Н, плотность жидкости ρ = 1000 кг/м3, x = 1,0 м, y = 0,8 м , d = 10 см, D = 40 см (рис. 29).

Задача 2.3.31
Квадратное отверстие размером B = 1,0 м в вертикальной стенке резервуара закрыто плоским поворотным щитом, который прижимается к стенке (рис. 30) под действием груза массой m, расположенном на плече a = 1,5 м. Определить:
а) минимальную массу груза m, достаточную для удержания воды в резервуаре на уровне H = 2,0 м, если расстояние от верхней кромки отверстия до оси вращения щита h = 0,3 м;
б) какой наименьший вакуум pвак над водой в резервуаре будет удерживать щит без
груза?
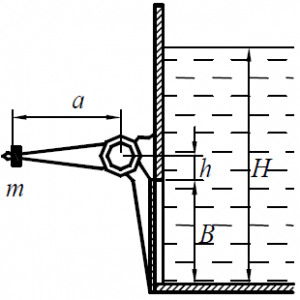
Задача 2.3.32
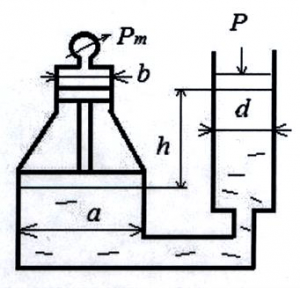
Покоящийся на неподвижном поршне и открытый сверху и снизу сосуд массой m = 16 кг состоит из двух цилиндрических частей, внутренние диаметры которых D = 0,5 м и d = 0,3 м (рис. 31). Определить, какой минимальный объём воды W должен содержаться в верхней части сосуда, чтобы сосуд всплыл над поршнем. Трением сосуда о поршень пренебречь.

Стоимость: 180 руб
Задача 2.3.33
Цилиндрический сосуд диаметром D = 0,2 м и высотой a = 0,4 м заполнен водой и опирается на плунжер диаметром d = 0,1 м (рис. 32). Определить показания манометра М и нагрузки на болтовые группы А и В, если масса верхней крышки сосуда m1 = 300 кг, масса цилиндрической части сосуда m2 = 150 кг, масса нижней крышки сосуда m3 = 120 кг.

Задача 2.3.34
В резервуаре на слое воды мощностью 1,2 м находится 6,6 м нефти плотностью 900 кг/м3. Диаметр резервуара равен 8 м. Определить давление на уровне дна резервуара и силу гидростатического давления, приложенную к его дну.
Задача 2.3.35
Прямоугольный поворотный затвор размерами a х b =1 х 2 (м) перекрывает выход из резервуара (рис. 33). На каком расстоянии x необходимо расположить ось затвора О, чтобы при открывании его в начальный момент необходимо было преодолевать только силы трения в шарнирах при глубине в резервуаре: а) H = 3,0 м; б) H = 4,0 м.
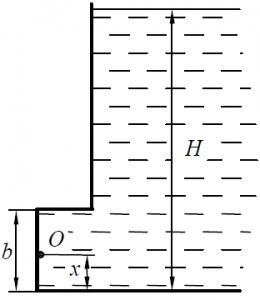
Задача 2.3.36
Как должны относиться диаметры поршня D/d, если поршень находится в равновесии при соотношении уровней z2 = 5z1 (рис. 34)?
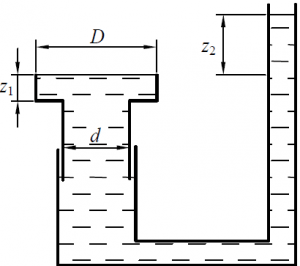
Задача 2.3.37
На какой высоте над манометром, присоединённым к резервуару, находится уровень нефти плотностью 840 кг/м3, если манометр показывает давление 1,21∙105 Па?
Задача 2.3.38
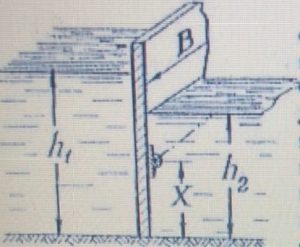
Определить реакцию крюка Rk, удерживающего прямоугольный щит шириной b = 1,0 м, при следующих данных: H1 = 4,2 м, H2 = 2,1 м, h = 0,5 м (рис. 35).

Задача 2.3.39
Какое избыточное давление испытывает водолаз, опустившийся на глубину 27 м?
Задача 2.3.40
Вычислить абсолютное давление в газопроводе, если заполненный водой манометр показывает вакуум 382 мм вод. ст., а барометрическое давление равно 752 мм рт. ст.
Задача 2.3.41
Прямоугольный щит шириной B = 2,0 м закреплён шарнирно в точке О (рис. 36). Определить усилие Т, необходимое для подъёма щита при H1 = 2,4 м, H2 = 1,5 м, h =1,0 м, α = 45°.
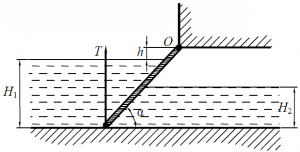
Задача 2.3.42
Определить величину и направление силы гидростатического давления на 1,0 м ширины затвора, представляющего собой четверть кругового цилиндра (рис. 37) радиусом R =1,5 м.
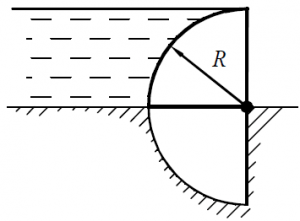
Задача 2.3.43
Найти величину и направление силы давления воды на 1,0 м ширины затвора (рис. 38), если R = 1,0 м, H = 2,0 м.
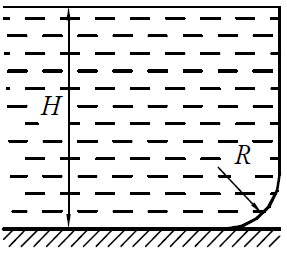
Задача 2.3.44
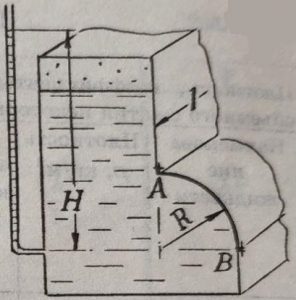
Внизу вертикальной стенки резервуар с водой имеет фасонную часть в виде четверти поверхности цилиндра (рис. 39). Определить величину и направление силы давления воды на 1,0 погонный метр ширины фасонной части, если R = 1,2 м, H = 3,0 м.

Задача 2.3.45
Тело, погружённое в воду, потеряло 1/8 своего веса. Определить плотность тела.
Задача 2.3.46
Вес поплавка в воздухе 721 Н. Вес поплавка, погружённого в воду, 561,7 Н. Какова плотность исследуемой жидкости, если погруженный в неё поплавок весит 537,9 Н?
Задача 2.3.47
Показания манометра, присоединённого к днищу бака, 10 кПа (рис. 40). Найти: а) давление воздуха pв, находящегося над водой, если h1 = 1,8 м, h2 = 1,0 м;
б) растягивающее усилие болтов P, крепящих в вертикальной стенке бака коническую крышку диаметром d = 0,8 м. Массой крышки пренебречь.

Задача 2.3.48
Определить площадь плоской льдины толщиной h = 0,4 м, способной удержать груз G = 21,1 кН. Плотность льдины 920 кг/м3.
Задача 2.3.49
Монолитная плита весит в воздухе 2000 Н, а в воде 800 Н. Определить удельный вес монолита.
Задача 2.3.50
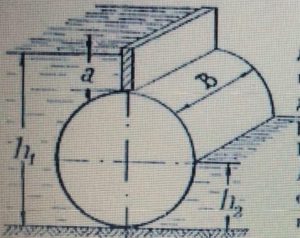
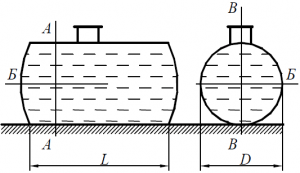
Лежащий на земле цилиндрический резервуар (рис. 41) диаметром D = 200 см и длиной L = 600 см заполнен керосином с удельным весом γ = 8 200 Н/м3. Горловина резервуара открыта. Вычислить усилия, разрывающие резервуар по сечениям А–А, Б–Б, В–В.
Задача 2.3.51
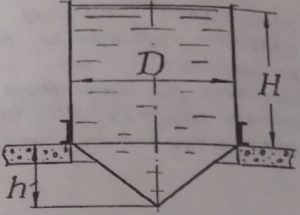
Перевёрнутая тяжёлая воронка размерами D = 20 см, h = 10 см, H = 20 см поставлена на ровную горизонтальную поверхность, покрытую листовой резиной. Узкое отверстие воронки заканчивается тонкой трубкой, через которую можно наливать внутрь воронки воду (рис. 42). При какой массе m вода начинает вытекать из-под воронки?

Задача 2.3.52
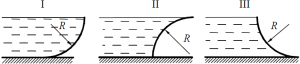
Определить величину и направление силы давления воды на 1,0 погонный метр ширины затвора, представляющего собой четверть кругового цилиндра (рис. 43) радиусом R = 3,0 м.
Стоимость: 200 руб
Задача 2.3.53
Определить потребное число пустых бочек для устройства плота и переправы на нём через реку машины с грузом G = 21 кН, если диаметр бочки D = 0,7 м, длина бочки l = 1,2 м, вес одной бочки q = 500 Н.
Стоимость: 180 руб
Задача 2.3.54
Рассчитать плот из бочек, скреплённых 10 брёвнами диаметром d = 240 мм и 20 досками сечением 200 х50 мм для переправы груза массой 2000 кг, если плотность древесины 800 кг/м3, длина плота L = 6,0 м, вес одной бочки q = 300 Н и объём одной бочки W= 200 л.
Стоимость: 180 руб
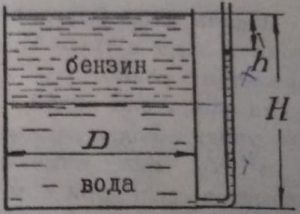
Задача 2.3.55
Ареометр весом 0,52 Н погружён в нефть плотностью 870 кг/м3 до отметки А и в воде до отметки B (рис. 44). Определить расстояние h между отметками А и B, если диаметр шейки ареометра равен 10 мм.

Задача 2.3.56
Бетонная плита весит в воздухе 1230 Н, а в воде 735 Н. Определить удельный вес бетона.
Задача 2.3.57
С целью определения удельного веса неизвестного сплава слиток его взвесили дважды: один раз в воздухе, другой раз – погрузив в воду. Вес слитка в воздухе 0,164 кгс. Вес слитка в воде 0,150 кгс. Вычислить удельный вес сплава.
Задача 2.3.58
Сколько брёвен диаметром d = 300 мм и длиной l = 10,0 м необходимо для сооружения плота, способного удержать груз весом G = 2,6 кН? Плотность древесины 840 кг/м3.
Задача 2.3.59
Ареометр (рис. 45) весом 0,56 Н в рассоле с удельным весом γ1 = 11600 Н/м3 погружён до отметки B, а в рассоле с удельным весом γ2 = 11900 Н/м3 – до отметки А. Вычислить расстояние h между отметками А и B, если диаметр шейки ареометра равен 6 мм.
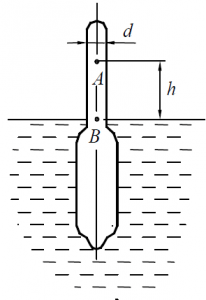
Задача 2.3.60
Нефтеналивное судно прямоугольного сечения с плоским дном длиной 100,0 м и шириной 20,0 м с полным грузом имеет осадку 2,5 м, а без груза – 400 мм. Определить массу нефти, перевозимой судном. Плотность морской воды принять равной 1000 кг/м3.
Задача 2.3.61
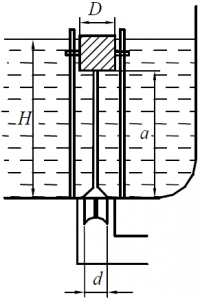
Уровень жидкости в резервуаре регулируется клапаном, связанным с поплавком, имеющим форму цилиндра с вертикальной осью (рис. 46). Размеры поплавка и клапана следующие: D = 200 мм, d = 30 мм, a = 1500 мм. Масса поплавка с клапаном равна 2,06 кг. В резервуар поступает нефть плотностью 880 кг/м3. Определить, при какой высоте уровня жидкости H откроется клапан. Толщиной тяги, соединяющей поплавок с клапаном, пренебречь.
Задача 2.3.62
В бурящейся скважине находится бурильный инструмент, масса которого 88 т. Плотность глинистого раствора 1180 кг/м3. Определить нагрузку, испытываемую крюком, если ρст = 7850 кг/м3.
Задача 2.3.63
Плоскодонная металлическая баржа длиной 36 м и шириной 10 м с грузом песка имела осадку 1 м. После выгрузки песка осадка баржи стала равной 25 см. Определить массу выгруженного песка, если объёмный вес его равен 2∙103 дин/см3.
Задача 2.3.64
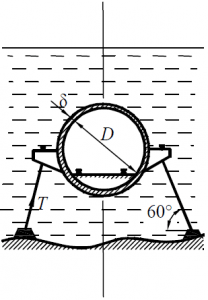
Подводный железобетонный тоннель круглого сечения с внутренним диаметром D = 3,0 м и толщиной стенки δ = 250 мм удерживается от всплытия тросами Т, расположенными попарно через каждые 6,0 м длины тоннеля (рис. 47). Определить натяжение тросов, принимая, что дополнительная нагрузка, приходящаяся на 1,0 м длины тоннеля, равна G = 10 кН, а плотность бетона равна 2,5 т/м3.
Задача 3.6.65
Вычислить вес 800 погонных метров стальных насосных штанг диаметром 3/4″, опущенных в скважину, заполненную нефтью с удельным весом 900 кгс/м3, если известно, что 1 погонный метр таких штанг с муфтами весит на воздухе 2,4 кгс. Плотность стали принять равной 7 800 кг/м3.
Пример к случаю 1
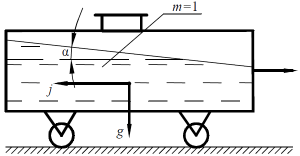
При торможении вагона-цистерны, частично заполненной нефтью, возникло ускорение a = -2 м/с2. Определить угол наклона свободной поверхности нефти к горизонту.
Стоимость: 90 руб
Случай 2
Открытый цилиндрический сосуд (рис. 49), наполненный жидкостью, вращается вокруг своей вертикальной оси с постоянной угловой скоростью ω. Жидкость в этом случае будет вращаться с той же угловой скоростью и, следовательно, по отношению к стенкам сосуда будет в состоянии покоя.
Пример к случаю 2
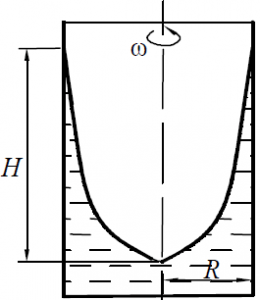
В цилиндрическую форму (рис.50) высотой L = 1000 мм и внутренним диаметром D = 1120 мм, вращающуюся при n = 500 об/мин, залит цементный раствор (литой) с удельным весом γ = 1 600 кгс/м3 для изготовления трубы центробежным способом. При толщине стенки цементной трубы δ1 = 60 мм определить толщину стенки трубы δ2 у верхней торцовой стенки формы.
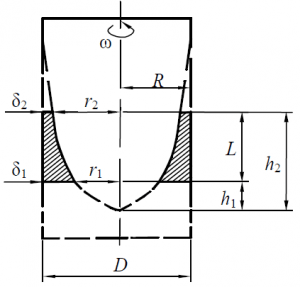
Стоимость: 120 руб
Пример к случаю 3
В открытом канале шириной B = 20 м поток воды движется со средней скоростью V = 3 м/с. Определить разность отметок горизонтов воды у противоположных берегов на повороте канала, если радиус кривизны оси канала R0 = 70 м.
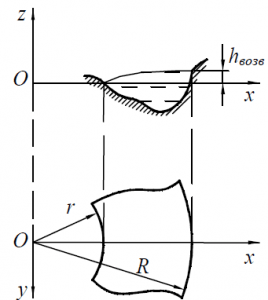
Стоимость: 90 руб
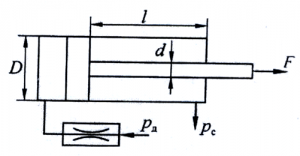
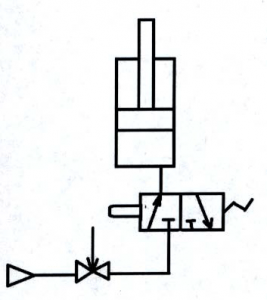
Пример 1
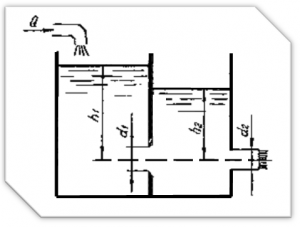
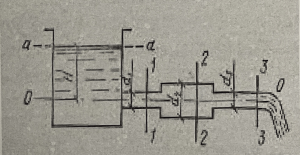
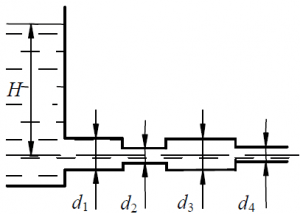
Определить скорость на всех участках трубопровода переменного сечения, присоединённого к резервуару (рис.52), расход и построить пьезометрическую и напорную линии. Расстояние от свободной поверхности воды в резервуаре до центра тяжести выходного сечения трубопровода H = 10 м. Манометрическое давление на поверхности воды в резервуаре p = 0,6 ат. Диаметры трубопровода на соответствующих участках: d1 = 125 мм, d2 = 63 мм, d3 = 100 мм, d4 = d5 = 75 мм. Вода из трубопровода вытекает в атмосферу. Решить задачу без учёта сопротивлений (жидкость идеальная).

Стоимость: 210 руб
Пример 2
Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d = 12 мм и максимальный диаметр d = 3500 мм. Расчётные скорости движения воды в них V = 0,5÷4,0 м/с. Определить минимальное и максимальное значения чисел Рейнольдса и режим движения воды в этих трубопроводах.
Стоимость: 90 руб
Пример 3
По трубопроводу постоянного поперечного сечения перекачивается жидкость плотностью ρ = 950 кг/м3. Избыточное давление в начале трубопровода p1 = 3∙105 Па. Пренебрегая потерями напора при движении жидкости, определить максимальный угол наклона трубопровода к горизонту, чтобы давление в конце трубопровода было равно атмосферному. Длина трубопровода равна 5 км.
Стоимость: 90 руб
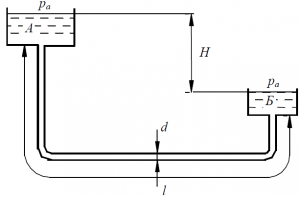
Пример 4
По самотечной железобетонной трубе длиной l = 100 м из водоёма А в колодец Б поступает вода с расходом Q = 150 л/с (рис.53). При входе в трубу устроена сетка. Разность горизонтов в водоёме и колодце не должна превышать H ≤ 0,4 м. Скорость в трубе V ≤ 1,0 м/с. Определить необходимый диаметр такой самотечной трубы.
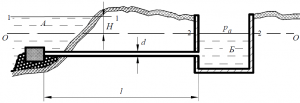
Стоимость: 210 руб
Пример 5
Определить диаметр железобетонного дюкера (рис.54), проложенного под автомобильной дорогой, и разность между подпорным и бытовым горизонтами, если длина дюкера L = 50 м, расход воды в дюкере Q = 2,5 м3/с и допускаемая скорость V= 3,0 м/с.

Стоимость: 120 руб
Пример 6
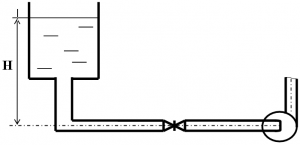
Центробежный насос А (рис.55) засасывает воду из колодца Б по трубе длиной l = 30,0 м в количестве Q = 65,0 л/с и нагнетает эту воду по трубе длиной L = 200 м на высоту h = 20,0 м в напорный бак В. Всасывающая труба при входе имеет сетку и обратный клапан. На нагнетательной трубе поставлена задвижка с открытием s/d=7/8. Допускаемая скорость в трубопроводе Vдоп = 1,0 ÷ 2,0 м/с. Коэффициент полезного действия насоса η = 0,8.
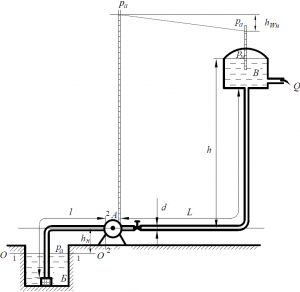
Стоимость: 210 руб
Пример 7
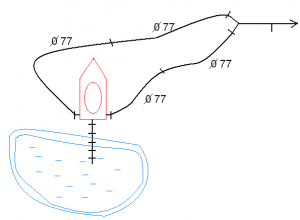
Подобрать диаметры участков трубопровода, изображённого на рис. 56, и установить необходимую высоту водонапорной башни при следующих данных: lАБ = 600 м, lБВ = 300 м, lВГ = 250 м, lБД = 400 м, lВЖ = 150 м, lЖЕ = 150 м, lЖЗ = 200 м; расходы в конце участков QГ = 18 л/с, QЗ = 12 л/с, QЕ = 16 л/с, QД = 30 л/с. Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор hсв = 12 м.

Стоимость: 210 руб
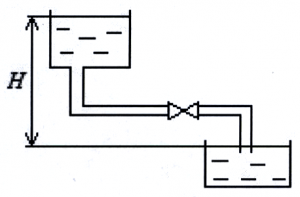
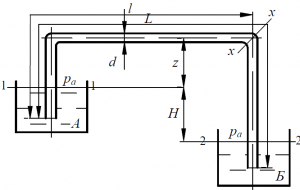
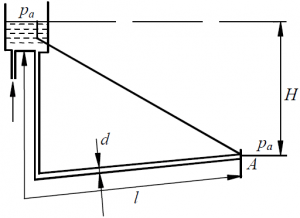
Пример 8
По сифону диаметром d = 100 мм (рис. 57), длина которого L = 20 м, вода в количестве Q = 10 л/с переливается из резервуара А в резервуар Б. Определить разность горизонтов воды в резервуарах А и Б и величину наибольшего вакуума в сифоне. Расстояние от уровня воды в резервуаре А до центра сечения x–x равно z = 3,0 м, а расстояние от начала сифона до сечения x–x равно l = 15,0 м. Коэффициент шероховатости старых стальных труб сифона n = 0,0125. Кинематическую вязкость воды принять ν = 0,0131 см2/с.
Стоимость: 210 руб
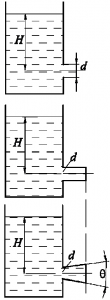
Пример 9
Определить расход воды из круглого отверстия диаметром d = 10 см и установить, как он изменится, если к этому отверстию присоединить цилиндрический насадок длиной l = 0,4 м или конически расходящийся насадок с углом конусности θ = 6º (рис. 58). Напор над центром тяжести отверстия H = 3,0 м.
Стоимость: 120 руб
Задача 3.3.1
Трубопровод состоит из трёх последовательно соединённых участков труб, внутренние диаметры которых d1 = 52 мм, d2 = 76 мм, d3 = 82 мм. Определить средние скорости жидкости на участках, если объёмный расход в трубопроводе Q = 48 л/мин.
Задача 3.3.2
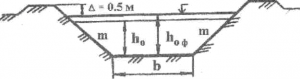
Вычислить гидравлический радиус потока воды в открытом канале трапецеидального сечения с размерами: b = 3,0 м, h = 1,0 м, α = 45° (рис. 59).

Задача 3.3.3
Для потока жидкости в трубе квадратного сечения с размерами 1,0 × 1,0 м вычислить значения гидравлического радиуса при заполнении трубы жидкостью до высоты h = 0,2; 0,4; 0,6; 0,8; 1,0 м. Построить график изменения гидравлического радиуса R в зависимости от высоты уровня h жидкости в трубе.
Задача 3.3.4
По трубопроводу диаметром d = 100 мм перекачивается нефть с расходом Q = 12,0 дм3/с. Определить режим движения жидкости и критическую скорость при температуре t = 10 °C.
Задача 3.3.5
Определить давление жидкости в сечении 2–2 при удельном весе γ = 9000 Н/м3. Известно, что в сечении 1–1 скорость равна V1= 1 м/с, давление p1 = 3,0 ат. Площадь в сечении 1–1 в 3 раза больше площади в сечении 2–2. Жидкость считать идеальной.
Задача 3.3.6
Определить среднюю скорость движения воды (рис. 60) в сечении 2–2, если в сечении 1–1 скорость V1 = 1,2 м/с, давление p1 = 1,2 ат. Давление в сечении 2–2 p2 = 1,1 ат. Центр тяжести сечения 2–2 находится ниже центра тяжести сечения 1–1 на величину h = 3,0 м. Потери давления на преодоление гидравлических сопротивлений равны hW= 1,4 м.
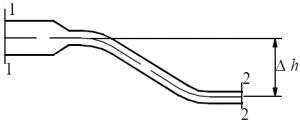
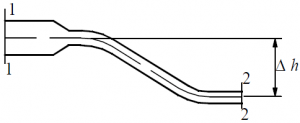
Задача 3.3.7
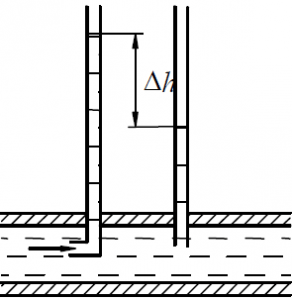
Вычислить давление в сечении 1–1 трубопровода, по которому движется жидкость плотностью ρ = 880 кг/м3 (см. рис.60). Известно, что скорость жидкости в сечении 1–1 трубопровода равна V1 = 1,1 м/с, площадь в сечении 1–1 в 2,5 раза больше площади в сечении 2–2. Разность геометрических высот центров тяжести сечений принять равной Δh = 8,7 м. Жидкость считать идеальной.
Задача 3.3.8
Определить потери напора при подаче воды через трубку диаметром d = 2 см и длиной l = 20,0 м со скоростью V = 12 см/с при температуре t = 16˚C.
Задача 3.3.9
Для потока жидкости прямоугольного сечения с площадью живого сечения ω = 1,2 м2 найти такие размеры потока b и h, чтобы гидравлический радиус был наименьшим.
Задача 3.3.10
Для измерения скоростных напоров применяется гидрометрическая трубка (рис. 61), состоящая из пьезометра и трубки Пито. Определить местную скорость движения жидкости в трубопроводе, если разность показаний в трубке Пито и пьезометре равна Δh = 620 мм. Жидкость считать идеальной.
Задача 3.3.11
В сужающуюся трубу подаётся вода расходом Q = 0,065 л/с при температуре t =10˚C. Определить режим движения в широкой и узкой части, если d1 = 40 мм и d2 = 20 мм. Ответ: в широкой части режим ламинарный; в узкой части режим турбулентный.
Стоимость: 120 руб
Задача 3.3.12
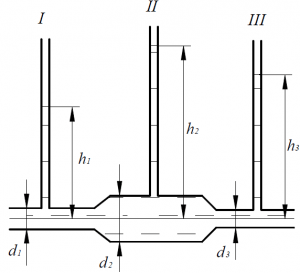
Горизонтальный трубопровод составлен из трёх участков различных диаметров (рис. 62): d1 = 24 мм, d2 = 56 мм, d3 = 40 мм. Высота уровней в пьезометрических трубках I и II при движении жидкости по трубопроводу устанавливается соответственно: h1 = 68 см и h2 = 84 см. Вычислить пьезометрическую высоту h3, установившуюся в пьезометре III. Жидкость считать идеальной.
Задача 3.3.13
Из резервуара вытекает вода по трубопроводу переменного сечения с площадями ω1 = 5,0 м2, ω2 = 0,015 м2, ω3 = 0,04 м2, ω4 = 0,02 м2 (рис. 63). Расстояния от плоскости сравнения до центра тяжести сечений соответственно: z1 = 4,0 м, z2 = 2,0 м, z3 = 0,5 м, z4 = 0. Абсолютное давление на поверхности жидкости в резервуаре pА = 110 кПа. Определить расход воды, скорость и избыточное давление давление жидкости (в метрах водного столба) в сечениях жидкости (в напорную и пьезометрическую линии. Движение по трубопроводу считать установившимся. Потерями напора пренебречь.
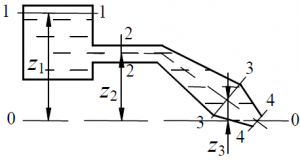
Задача 3.3.14
Из открытого резервуара с постоянным расходом Q = 1,0 л/с и скоростью V = 0,5 м/с подаётся нефть (рис.64 ) Определить диаметр d и напор H, необходимый для пропуска нефти по трубопроводу длиной L = 100 м. Кинематическую вязкость нефти принять равной = 0,14 см2/с. Построить напорную и пьезометрическую линии.
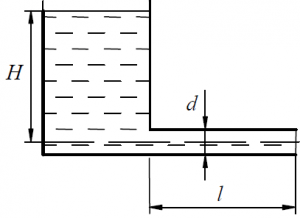
Задача 3.3.15
Вычислить потерю напора в трубопроводе внутренним диаметром d = 50 мм, длиной L = 100 м при перекачке нефти с кинематической вязкостью = 0,2 Ст и скоростью движения V = 0,3 м/с.
Задача 3.3.16
Нефть с кинематической вязкостью = 0,3 см2/с движется по трубопроводу. Определить минимальный диаметр трубопровода d, при котором нефть будет двигаться при ламинарном режиме с расходом Q = 8,14 л/с.
Задача 3.3.17
Определить расход воды в горизонтальном трубопроводе переменного сечения, скорость на каждом из участков и построить пьезометрическую линию, если H = 5 , 0 м , d 1 = 1 2 0 м м , d2 = d4= 60 мм, d3 = 100 мм (рис. 65).
Задача 3.3.18
Определить путевые потери в водопроводе диаметром d = 80 мм и длиной L = 250 м, если расход воды составляет Q = 8,0 л/с и температура воды t = 12˚C. Эквивалентную шероховатость принять равной Δ = 0,25 мм.
Задача 3.3.19
Из открытого бака с постоянным напором H = 11,0 м по чугунному трубопроводу длиной L = 3,5 м и диаметром d = 80 мм вода вытекает в атмосферу (см. рис. 64). Определить скорость и расход, пренебрегая местными потерями. Коэффициент гидравлического трения принять равным λ = 0,02.
Задача 3.3.20
Нефть с кинематической вязкостью ν = 0,3 см2/с движется по трубопроводу. Найти:
а) минимальный диаметр трубопровода, при котором нефть будет двигаться при ламинарном режиме с расходом Q = 8,14 л/с; б) с каким расходом нефть будет двигаться по трубопроводу с диаметром d = 150 мм при числе Рейнольдса Re = 5000.
Задача 3.3.21
По нефтепроводу диаметром d = 200 мм и длиной l = 4,0 км перекачивается нефть с расходом Q = 108 м3/ч, кинематической вязкостью ν = 1 Ст, удельным весом γ = 8829 Н/м3. Определить необходимое давление в начале нефтепровода:
а) при горизонтальной местности;
б) если местность имеет уклон в сторону движения нефти i0 = 0,001.
Задача 3.3.22
Определить потерю напора в нефтепроводе диаметром 200 мм и длиной 50 км при перекачке нефти вязкостью 3,5 Ст. Абсолютную шероховатость труб принять равной 0,12 мм. Расход нефти равен 42 л/с.
Задача 3.3.23
Определить потерю напора на трение по длине водопровода диаметром d = 100 мм и длиной L = 2,5 км, если расход воды составляет 118 л/с.
Задача 3.3.24
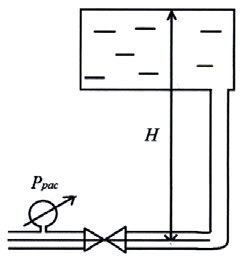
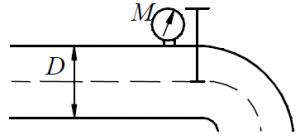
При закрытом кране манометр показывает давление p1 = 4,0 ат. После открытия крана манометр стал показывать давление p2 =1,5 ат (рис. 66). Определить расход, если диаметр трубы D = 100 мм.
Задача 3.3.25
По трубопроводу диаметром d = 150 мм перекачивается нефть, кинематическая вязкость которой ν = 2,8∙10-6 м2/с. Приняв режим движения нефти при расходе Q = 44 дм3/с ламинарным, определить гидравлический уклон потока.
Задача 3.3.26
По стальному трубопроводу длиной 250 м и диаметром 100 мм перекачивается нефть со скоростью 2,1 м/с. Динамическая вязкость нефти μ = 3,3 сП (сантипуаз), плотность нефти ρ = 890 кг/м3. Определить гидравлический уклон. Построить напорную линию.
Задача 3.3.27
Определить расход при подаче разжиженного битума по трубопроводу при условии сохранения ламинарного режима движения, если диаметр d = 100 мм, кинематическая вязкость битума ν = 0,02 Ст.
Задача 3.3.28
По трубопроводу диаметром d = 80 мм и длиной l = 1000 м подаётся разогретый битум вязкостью ν = 0,8 Ст. Определить потери напора в трубопроводе, если расход Q = 8 л/с.
Задача 3.3.29
По трубопроводу постоянного диаметра и длиной L = 56,4 км перекачивается нефть плотностью ρ = 860 кг/м3. Начальная точка выше конечной точки на 120 м. Определить гидравлический уклон, если известно, что давление в начальной точке p1 = 3,0∙106 Па, а в конечной точке p2 = pа.
Задача 3.3.30
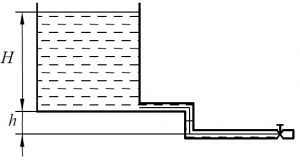
Из водоёма с минимальной высотой уровня H = 2,0 м вода отводится по трубе диаметром d = 100 мм (рис. 67) с расходом Q = 20 дм3/с. На пути движения воды имеются местные сопротивления: вход в трубу, два резких поворота на 90˚, одна полностью открытая задвижка. Длина участка трубы l = 210,0 м. Определить высоту h, на которую нужно поднять резервуар, чтобы обеспечить пропуск данного расхода. Построить пьезометрическую и напорную линии.
Задача 3.3.31
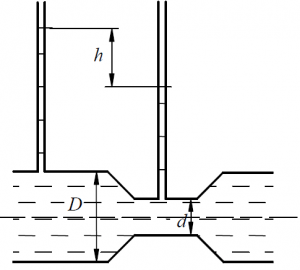
По трубчатому расходомеру протекает вода (рис. 68) с расходом Q = 9,0 л/с. Диаметр суженной части трубопровода составляет d = 50 мм.
Определить:
а) разность показаний пьезометров h, если диаметр основного трубопровода D = 75 мм;
б) диаметр основного трубопровода D, если разность показаний пьезометров h = 1,03 м.
Задача 3.3.32
По трубопроводу постоянного сечения длиной l = 5800 м перекачивается нефть плотностью ρ = 890 кг/м3. Начальная точка трубопровода находится ниже конечной точки на 42,0 м. Гидравлический уклон равен I = 0,006. Определить необходимое давление p1 в начальной точке трубопровода, для получения избыточного давления в конечной точке p2 = 2 ат.
Задача 3.3.33
Определить диаметр трубы и необходимый напор для обеспечения пропуска расхода нефти Q = 1,0 л/с при скорости движения V = 0,5 м/с.
Построить пьезометрическую и напорную линии. Кинематическая вязкость нефти ν = 1,4 Ст. Длина трубы l = 100 м.
Задача 3.3.34
Определить напор центробежного насоса, зная расход Q = 100 л/с, коэффициент полезного действия насоса η = 0,65 и мощность на валу насоса N = 60 кВт.
Задача 3.3.35
Определить диаметр всасывающей трубы и вакуум у центробежного насоса, если известно, что расход Q = 17,7 л/с, расстояние от свободной поверхности в резервуаре до оси насоса hн = 6,0 м, длина всасывающей трубы lвс = 60,0 м, допустимая скорость в трубе V = 1,0 м/с (рис. 69). При входе во всасывающую трубу устроена сетка и обратный клапан.
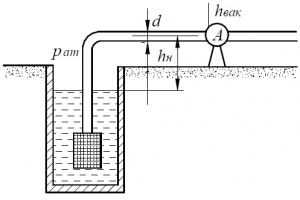
Задача 3.3.36
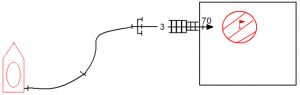
Насос откачивает бензин из подземного резервуара по всасывающему трубопроводу (рис. 70), диаметр которого d = 100 мм, длина l = 120,0 м, эквивалентная шероховатость Δ = 0,1 мм. Уровень бензина в резервуаре ниже оси насоса на H = 3,8 м. Давление на поверхности бензина в резервуаре атмосферное. Определить расход бензина из резервуара, если известно, что абсолютное давление всасывания насоса pвс = 42 кПа. Плотность бензина принять ρ = 750 кг/м3 и кинематическую вязкость ν = 0,01 Ст. Местные потери напора в трубопроводе считать равными 10% от путевых потерь.
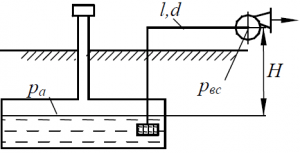
Задача 3.3.37
Определить силу P, которую нужно приложить к поршню насоса диаметром D = 65 мм, чтобы подавать в напорный бак жидкость с постоянным расходом Q = 2,5 л/с (рис. 71). Высота подъёма жидкости в установке H = 10,0 м. Избыточное давление в напорном баке p0 = 0,15 МПа; длина трубопровода l = 60,0 м, диаметр d = 30 мм, его шероховатость Δ = 0,03 мм. Коэффициент сопротивления вентиля на трубопроводе ζ = 5,5. Потери напора на плавных поворотах трубопровода не учитывать. Трением поршня в цилиндре пренебречь. Задачу решить для случаев подачи в бак бензина (ρ = 765 кг/м3, ν = 0,4 сСт) и машинного масла (ρ = 930 кг/м3, ν = 20 сСт).
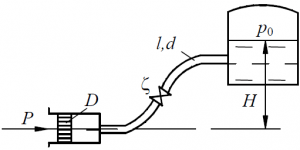
Задача 3.3.38
Керосин перекачивается насосом по резиновому шлангу длиной 160 м, диаметром 62 мм. Производительность насоса Q = 250 л/мин. Вычислить развиваемое насосом давление, если выкидной конец шланга открыт в атмосферу и поднят на 16,0 м выше нагнетательного патрубка насоса. Перекачиваемый керосин имеет вязкость ν = 0,024 Ст и плотность ρ = 800 кг/м3.
У к а з а н и е. Коэффициент Дарси для резиновых шлангов вычисляют по формуле λ = 0,0113 + 0,9170 Re-0,41.
Задача 3.3.39
Насос забирает из водоёма воду с температурой 20ºС в количестве Q = 50 л/с. Определить максимальную высоту расположения горизонтального вала насоса над свободной поверхностью воды, если давление перед насосом p2 = 0,3∙105 Па. На всасывающей чугунной трубе диаметром d = 0,25 м и длиной l = 50,0 м имеется заборная сетка, плавный поворот радиусом R = 0,5 м и регулирующая задвижка, открытая на 45% площади проходного сечения.
Задача 3.3.40
С помощью насоса, установленного в пункте А, в бак B подаётся нефть плотностью ρ = 905 кг/м3 (рис. 72). Высота всасывающей линии h = 4,0 м, высота нагнетательной линии H = 46,0 м. Давление в колодце и резервуаре атмосферное. Расход нефти равен Q = 12 м3/ч. Потери напора на преодоление гидравлических сопротивлений составляют 4,5 м. Определить мощность, потребляемую насосом, если коэффициент полезного действия насоса равен 75%.
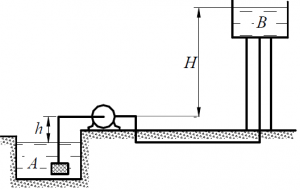
Задача 3.3.41
Вода из скважины по сифонному трубопроводу подаётся в сборный колодец. Длина трубы сифона 350 м, её диаметр 100 мм. Разность уровней воды в скважине и в колодце 2,2 м. Превышение наивысшей точки сифона над уровнем воды в скважине h = 2,8 м. Приняв коэффициент гидравлического трения λ = 0,025 и сумму коэффициентов местных сопротивлений 6,5, определить среднюю скорость движения воды и расход в сифонной трубке, а также вакуум в наивысшей точке сифона. Длина восходящей ветки 80,0 м.
Задача 3.3.42
По сифонному трубопроводу из скважины в сборный коллектор должна подаваться вода в количестве 5 л/с. Длина трубопровода 120 м, диаметр 76 мм, превышение наивысшей точки сифона над уровнем воды в скважине 3,1 м. Определить необходимый напор сифона, приняв сумму коэффициентов местных сопротивлений 7.
Задача 3.3.43
Сифонный бетонный водосброс диаметром d = 1,0 м, общей длиной L = 50,0 м сбрасывает воду из водохранилища в реку, уровень которой на H = 5,0 м ниже уровня водохранилища (рис. 73). Определить подачу сифонного водосброса Q, если он имеет два поворота: α = 90º и α = 45º с радиусами закругления R = 2,0 м. Длина горизонтального участка lг = 2,0 м. Температура воды в водохранилище 0ºС. Определить также вакуум в верхней точке сифона, если z1 = 3,0 м и z2 = 1,0 м.
Задача 3.3.44
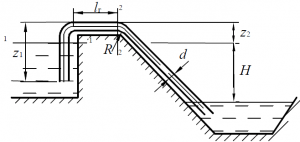
По самотечному сифонному трубопроводу длиной l = 44,0 м необходимо обеспечить расход нефти (ρ = 0,9 г/см3, ν = 1,0 Ст) Q = 1,0 л/с при напоре Р = 2,0 м (рис. 74). Найти требуемый диаметр D трубопровода, учитывая только потери напора на трение по его длине. Определить допустимое превышение h сечения К-К над уровнем в верхнем резервуаре, если это сечение находится на середине длины трубопровода, а вакуум не должен превышать pвак = 53 кПа.
Задача 3.3.45
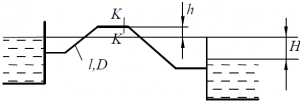
По сифону, изображённому на рис.75, перекачивается вода. Определить допустимую температуру воды для работы сифона без срыва потока при следующих данных: длина трубы 150 м, длина восходящей ветви сифона 24 м, превышение точки С над уровнем воды в верхнем резервуаре h = 4,0 м, H = 25,0 м. Скоростным напором можно пренебречь.
Задача 3.3.46
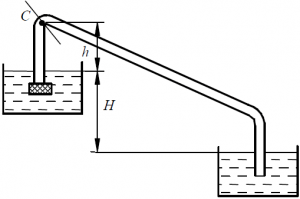
Определить требуемый напор в точке А для пропуска 25 л/с воды по замкнутому трубопроводу, изображённому на рис. 76, при следующих данных: напор в точке Б HБ = 15,0 м, диаметры участков d1 =150 мм, d2 = 100 мм, l1 = 1000 м, l2 = 600 м, l3 = 800 м.

Задача 3.3.47
Подобрать диаметры труб для участков замкнутой сети при следующих данных: длины участков l1 = 600 м, l2 = 500 м, l3 = 700 м; расходы на участках Q1 = 12 л/с, Q2 = 10 л/с, Q3 = 14 л/с; напор в точках А и Б равен HА = 15,0 м и HБ = 3,0 м (рис. 76).
Задача 3.3.48
Определить расходы в ветвях сети (см. рис. 75) при следующих данных: диаметры участков d1 = 100 мм, d2 = 150 мм, d3 = 76 мм, длины участков l1 = 1200 м, l2 = 900 м, l3 = 1600 м. Напор в точке А 40 м, напор в точке Б 5,0 м. Суммарная производительность сети 35 л/с.

Задача 3.3.49
Определить напор, необходимый для пропуска расхода воды Q = 0,07 м3/с через трубопровод диаметром d = 0,3 м и длиной l = 1200 м. Трубы стальные новые.
Задача 3.3.50
Определить приблизительный расход в стальном самотечном водопроводе диаметром d = 82 мм и длиной l = 820 м, если H = 12,9 м.
Задача 3.3.51
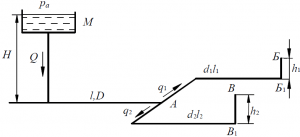
Из резервуара М по трубе длиной L = 1000 м в узел А (рис. 77) поступает вода в количестве Q = 12 л/с. В узле А трубопровод разветвляется, и расход q1 = 4,0 л/с пропускается по трубе длиной l1 = 75 м, а расход q2 = 8,0 л/с – по трубе длиной l2 = 100 м. Трубопроводы АБ1 и АВ1 расположены в горизонтальной плоскости, а точки Б и В подняты от этой плоскости соответственно на h1 = 8,0 м и h2 = 4,0 м. Из труб l1 и l2 вода вытекает в атмосферу. Вся сеть смонтирована из стальных цельнотянутых труб, и предполагается, что в процессе эксплуатации эти трубы можно будет отнести к разряду нормально загрязнённых (n = 0,0125). Определить диаметры труб на всех участках водопроводной сети и напор, необходимый для обеспечения пропуска заданных расходов.
Задача 3.3.52
Определить высоту водонапорной башни H над пунктом А, к которому вода подаётся по чугунным трубам, бывшим в употреблении, с расходом Q = 18 л/с. Длина водопровода l = 2000 м (рис. 78). В водонапорную башню вода подаётся насосом.
Задача 3.3.53
От водонапорной башни А проложен трубопровод из последовательно соединённых стальных новых труб разного диаметра. Вода из этого трубопровода в количестве Q = 5 л/с вытекает в атмосферу. В сечениях 1, 2, 3 и 4 отводятся соответствующие расходы: q1 = 4 л/с, q2 = 3 л/с,q3 =6 л/с и q4 = 2 л/с. Отдельные участки трубопровода имеют следующие длины: l1 = 1000 м, l2 = 750 м, l3 =1500 м, l4 = 1000 м, l5 = 1250 м. Определить высоту водонапорной башни и диаметры труб на участках трубопровода (рис. 79).

Задача 3.3.54
Определить разность горизонтов в резервуарах А и Б при расходе воды по трубопроводу, соединяющему эти резервуары, Q = 12∙10-3 м3/с. Длина трубопровода l = 400 м, диаметр d = 1000 мм (рис. 80). Коэффициент шероховатости следует принять n = 0,0125. Коэффициент Дарси определить с учётом области сопротивления. Местные потери составляют 10% потери напора по длине.
Задача 3.3.55
Определить, какое количество воды вытекло из цилиндрического вертикального резервуара диаметром D = 1,2 м за время t = 1 мин через отверстие в дне диаметром d = 100 мм. Уровень воды в баке поддерживается постоянным при напоре H = 1,3 м. Сжатие струи считать полным совершенным.
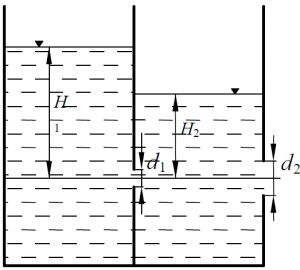
Задача 3.3.56
Призматический резервуар разделён на две части перегородкой (рис. 81). В левом отсеке поддерживается постоянный уровень воды. В перегородке имеется круглое отверстие диаметром d = 80 мм, расположенное на глубине H1 = 3,2 м под поверхностью воды. Во внешней стенке резервуара на одной высоте с первым отверстием расположено второе отверстие диаметром d2 = 100 мм Определить расход воды и уровень воды H2 в правом отсеке при установившихся уровнях в отсеках.
Задача 3.3.57
Цилиндрический резервуар диаметром D = 4,0 м и высотой H = 6,0 м имеет у дна отверстие диаметром d = 100 мм. Определить время полного опорожнения резервуара, если коэффициент расхода отверстия μ = 0,62.
Задача 3.3.58
Определить расход жидкости через цилиндрический насадок, имеющий диаметр d = 100 мм и длину l = 400 мм, если напор над центром насадка H = 3,4 м.
Задача 3.3.59
Вода вытекает через отверстие диаметром d = 25 мм в тонкой стенке вертикального цилиндрического резервуара, открытого сверху. Вычислить, за какой промежуток времени уровень воды в резервуаре снизится с 12,0 м до 4,5 м, считая от центра отверстия. Коэффициент расхода принять равным μ = 0,65, а диаметр бака D = 5,0 м.
Задача 3.3.60
В дне резервуара имеются два отверстия диаметром d = 100 мм. Напор поддерживается постоянным H = 2,0 м. Как изменится расход, если к одному из отверстий присоединить цилиндрический насадок?
Задача 3.3.61
С целью определения коэффициента расхода насадка, установленного в плоском днище вертикального цилиндрического открытого резервуара, наблюдали за понижением уровня воды в резервуаре. За 24 мин высота уровня понизилась от 2,6 м до 1,2 м. Диаметр резервуара D = 1,4 м, диаметр насадка d = 20 мм. Определить коэффициент расхода.
Задача 3.3.62
Через круглое незатопленное отверстие в тонкой стенке диаметром d = 40 мм вытекает вода. Каким должен быть напор воды над центром отверстия, чтобы её расход был равен Q = 2,6 л/с?
Задача 3.3.63
Определить расход воды через гидромонитор (конический насадок), выходное отверстие которого равно d = 40 мм, если манометр показывает давление 4 ат.
Задача 3.3.64
В резервуаре находится 1,1 м воды и 6,2 м нефти плотностью ρ = 900 кг/м3. Диаметр резервуара D = 6,0 м. Определить время слива воды через короткий патрубок диаметром d = 100 мм.
Задача 3.3.65
Определить расход воды через квадратное затопленное отверстие со стороной a = 150 мм, если глубина погружения центра отверстия под свободную поверхность с напорной стороны H1 = 4,4 м, а с низовой стороны H2 = 2,2 м. Скоростью подхода воды пренебречь.
Часть задач есть решенные, контакты