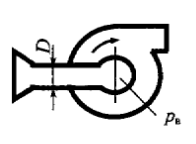РАрх
Задач, которых нет на странице, Вы можете заказать
Задача 1.1
Канистра (сосуд), наполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры t2 = 55°С. Определить приращение давления внутри канистры при условии, что она абсолютно жесткая. Начальная температура бензина t1 = 15°С. Модуль объемной упругости бензина E = 1300 МПа, коэффициент температурного расширения βt = 8 · 10-4 °С-1.
Купить задачу 1.1
Задача 1.5
Сосуд заполнен водой, занимающей объем V = 2 м3. Как изменится этот объем при увеличении давления на Δр = 3 МПа? Коэффициент объемного сжатия принять равным βр = 4,75 · 10-10 Па-1.
Купить задачу 1.5
Задача 1.7
Резервуар наполнен до краев нефтью при температуре t1 = 15 °C. Определить, какой объем ΔV нефти выльется при повышении температуры до t2 = 30 °C. Объем резервуара Vр = 1 м3. Коэффициент температурного расширения нефти βt = 0,00064 °C-1, а ее плотность ρ = 950 кг/м3.
Купить задачу 1.7
Задача 1.8
Как изменится объем воды в системе отопления, имеющей вместимость V = 100 м3, после подогрева воды от начальной температуры t1 = 15 °С до t2 = 95 °С. Коэффициент температурного расширения воды принять βt = 6 · 10-4 °С-1.
Купить задачу 1.8
Задача 1.10
В автоклав вместимостью V = 0,01 м3 наполнен водой и герметически закрыт. Определить, пренебрегая деформацией материала автоклава, повышение давления в нем при изменении (увеличении) температуры на Δt = 40 °C, если коэффициент температурного расширения воды βt = 0,00018 °C-1, а коэффициент объёмного сжатия βр = 4,19 · 10-10 Па-1.
Задача 1.11
Автоклав с диаметром цилиндрической части d = 1,5 м и длиной l = 3,5 м имеет днище и крышку в форме полусферы. Определить объем воды ΔV, который требуется дополнительно закачать в него для того, чтобы давление возросло от 0 до 100 МПа. Коэффициент объемного сжатия воды βp = 4,19 · 10-10 Па-1. Деформацией автоклава пренебречь.
Купить задачу 1.11
Задача 1.12
В автоклав вместимостью V = 0,05 м3 под давлением закачано V1 = 0,0505 м3 эфира. Определить, пренебрегая деформацией стенок автоклава, повышение давления Δp, если коэффициент объёмного сжатия эфира βр = 1,95 · 10-9 Па-1.
Купить задачу 1.12
Задача 1.13
Определить падение давления масла в напорной линии гидропривода вместимостью V = 0,15 м3, если утечки масла ΔV = 5 ∙ 103 м3, а коэффициент объёмного сжатия βр = 7,5 ∙ 1010 Па-1. Деформацией элементов гидропривода пренебречь.
Купить задачу 1.13
Задача 1.14
Определить повышение давления, при котором начальный объем воды уменьшится на 3%. Коэффициент объемного сжатия воды βp = 4,85 · 10-10 1/Па.
Купить задачу 1.14
Задача 1.21
При экспериментальном определении вязкости минерального масла вискозиметром получено: время истечения 200 см3 дистиллированной воды при температуре 20 °С t1 = 51,2 с, время истечения 200 см3 масла t2 = 163,4 с. Определить кинематический коэффициент вязкости масла.
Задача 1.34
Как изменится объем воды при увеличении высоты подъема его над уровнем моря от Н1 = 50 м до Н2 = 95 м. Коэффициент объемного сжатия воды βр = 5 · 10-10 Па-1.
Купить задачу 1.34
Задача 1.45
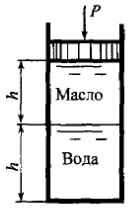
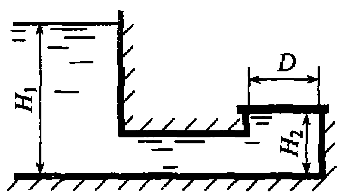
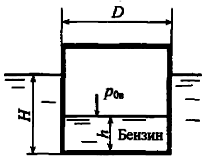
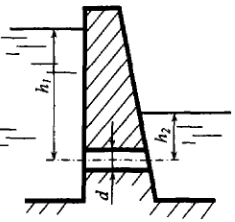
В цилиндрическом резервуаре находятся вода и минеральное масло, высота слоя каждой жидкости h = 400 мм (рис. 1.11). Пренебрегая деформацией резервуара, определить ход поршня, если давление в жидкости возросло на Δр = 5 МПа. Коэффициенты объёмного cжатия: воды βрв = 5 · 10-10 Па-1, масла βрм = 7,7 · 10-10 Па-1.
Купить задачу 1.45
Задача 1.53
Цилиндрический резервуар диаметром Dц =3м заполнен мазутом при температуре t1 = +15°С плотностью ρ = 920 кг/м3. Масса мазута т = 30000 кг. Определить высоту подъёма мазута в резервуаре, если его температура повысится до 42°С. Коэффициент температурного расширения мазута βt = 0,0008°С-1.
Купить задачу 1.53
Задача 1.60
Вязкость нефти, определенная по вискозиметру, составляет 12 °ВУ. Определить динамический и кинематический коэффициенты вязкости, если плотность нефти ρн = 870 кг/м3.
Купить задачу 1.60
Задача 2.1
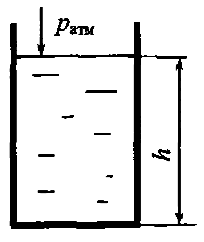
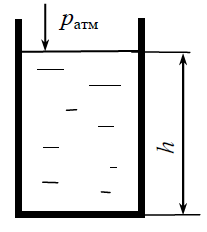
Определить избыточное и абсолютное давления в точке, расположенной на дне открытого резервуара (рис. 2.7), если уровень жидкости в резервуаре h = 2,0 м, плотность жидкости ρ = 103 кг/м3. Атмосферное давление pатм = 0,1 МПа.
Купить задачу 2.1
Задача 2.2
Определить высоту наполнения резервуара жидкостью с относительной плотностью δ = 0,85 (рис. 2.7), если в точке, расположенной на дне открытого резервуара, абсолютное давление рабс = 135 кПа. Атмосферное давление ратм = 0,1 МПа.
Купить задачу 2.2
Задача 2.3
Определить абсолютное и избыточное давление в точке А, расположенной на глубине h = 1,5 м, если плотность жидкости ρ = 800 кг/м3. Атмосферное давление pа = 750 мм рт. ст.
Купить задачу 2.3
Задача 2.5
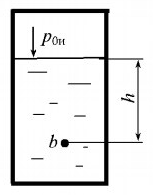
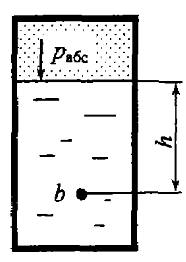
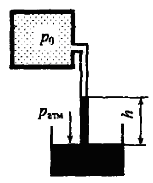
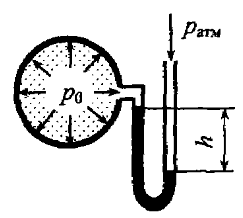
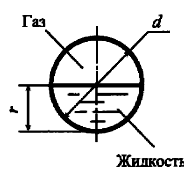
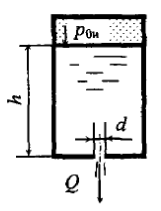
Определить избыточное давление газа p0и в резервуаре, если абсолютное давление в точке b равно 2 бара (рис. 2.9). Точка погружена в жидкость на глубину h = 2,0 м. Плотность жидкости ρ = 103 кг/м3.
Задача 2.9
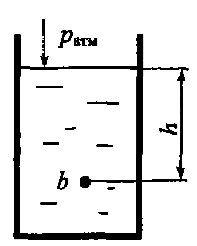
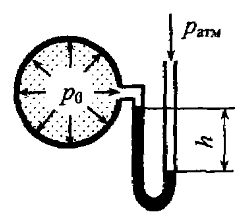
Определить абсолютное давление в точке b, которая находится на глубине h = 3,5 м, если абсолютное давление на поверхности жидкости в резервуаре равно 35 кПа (рис. 2.10). Относительная плотность жидкости δ = 1,05.
Купить задачу 2.9
Задача 2.11
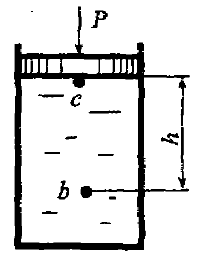
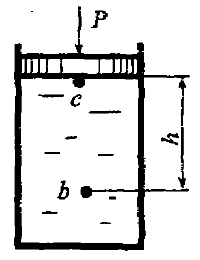
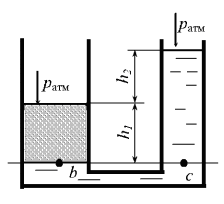
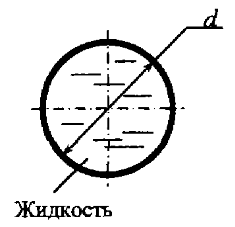
Определить абсолютное давление в точке с под поршнем и в точке b на глубине h = 1,3 м, если диаметр поршня d = 0,4 м, а сила, действующая на поршень, Р = 12 кН (рис. 2.11). Относительная плотность жидкости δ = 1,2.
Купить задачу 2.11
Задача 2.12
Определить избыточное давление в точке с под поршнем, а также, на какой глубине должна находиться точка b, чтобы избыточное давление в этой точке было в два раза больше, чем в точке с. Диаметр поршня d = 0,4 м, а сила, действующая на поршень, Р = 24 кН. Плотность жидкости ρ = 950 кг/м3 (рис. 2.11).
Купить задачу 2.12
Задача 2.16
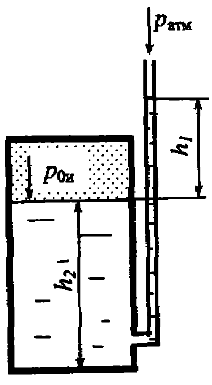
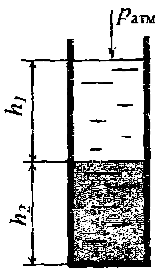
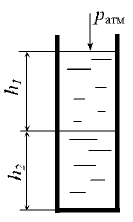
Определить избыточное давление р0и в закрытом резервуаре при условии: h1 = 0,6 м, плотность жидкости ρ = 900 кг/м3, атмосферное давление ратм = 0,1 МПа (рис. 2.14). Чему равно абсолютное давление на дно резервуара при h2 = 1,0 м. Построить эпюру избыточного давления на боковую поверхность резервуара.
Купить задачу 2.16
Задача 2.17
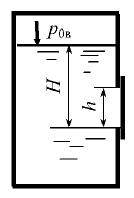
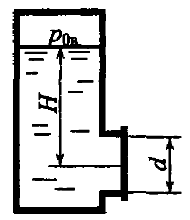
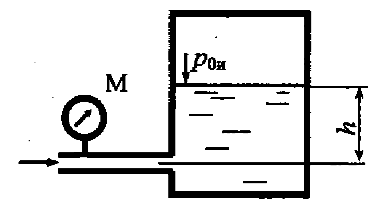
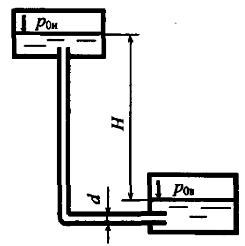
Определить, при каком значении вакуумметрического давления р0в в закрытом резервуаре жидкость поднимается на высоту h = 0,5 м (рис. 2.13); плотность жидкости ρ = 1100 кг/м3, атмосферное давление ратм = 0,1 МПа.
Купить задачу 2.17
Задача 2.21
Определить, на какой глубине h в открытом резервуаре избыточное давление составляет рн = 104 Па. Плотность жидкости ρ = 950 кг/м3 (рис. 2.8).
Купить задачу 2.21
Задача 2.22
Определить, на какой глубине в закрытом резервуаре абсолютное давление составляет р = 2 · 105 Па, если на поверхности воды избыточное давление составляет р0и = 35 кПа (рис. 2.17).
Купить задачу 2.22
Задача 2.23
Определить абсолютное и избыточное давление в точке, расположенной на дне отстойника (рис. 2.18). В отстойнике находятся две жидкости: внизу – глицерин, высота которого h2 = 0,4 м, а плотность ρг = 1250 кг/м3; вверху – масло, высота которого h1 = 1,3 м, а плотность ρм = 750 кг/м3.
Купить задачу 2.23
Задача 2.25
В отстойнике (рис. 2.18) находятся две жидкости: внизу — глицерин, относительная плотность которого δ = 1,25; вверху — вода, высота которой h1 = 0,75 м. Определить высоту столба глицерина h2, если избыточное давление в точке, расположенной на дне отстойника, р = 23 кПа.
Купить задачу 2.25
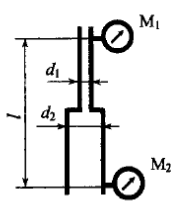
Задача 2.34
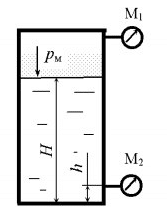
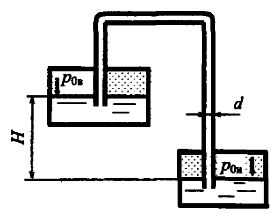
Определить уровень нефти Н (ρн = 900 кг/м3) в закрытом резервуаре, если манометры М1 и М2 показывают давление соответственно 0,2 · 105 и 1,1 · 105 Па, h = 0,2 м (рис. 2.22).
Купить задачу 2.34
Задача 2.42
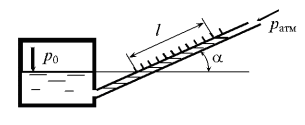
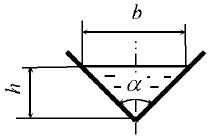
Для измерения малых давлений трубка пьезометра расположена наклонно под углом α = 30° (рис. 2.24). Относительная плотность жидкости δ = 0,8. Определить показание l при абсолютном давлении p0 = 1,01 · 105 Па. Смещением уровня жидкости в сосуде пренебречь.
Купить задачу 2.42
Задача 2.43
Для измерения малых давлений трубка пьезометра расположена наклонно под углом α = 30° (рис. 2.25). Относительная плотность жидкости δ = 0,8. Определить абсолютное давление p0, если показание l = 255 мм. Смещением уровня жидкости в сосуде пренебречь.
Купить задачу 2.43
Задача 2.46
К резервуару, заполненному минеральным маслом, присоединен пьезометр (рис. 2.26). Абсолютное давление на поверхности жидкости в резервуаре р0 = 1,18 кг/см2. Определить плотность минерального масла, если высота его подъема в трубке пьезометра h = 2,0 м.
Купить задачу 2.46
Задача 2.49
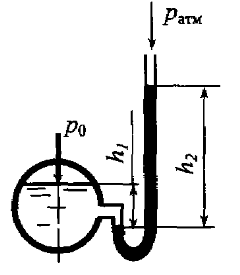
Определить абсолютное давление p0 на поверхности воды в трубке (рис. 2.27), если высота подъема ртути в трубке h2 = 0,28 м (ρрт = 13600 кг/м3), а высота до поверхности воды в трубке h1 = 0,15 м.
Купить задачу 2.49
Задача 2.51
Определить вакуумметрическое давление в сосуде (рис. 2.28), если уровень ртути в вакуумметре h = 0,15 м.
Купить задачу 2.51
Задача 2.52
Определить показание ртутного вакуумметра h (рис. 2.28), если вакуумметрическое давление в сосуде pв = 24,5 кПа.
Купить задачу 2.52
Задача 2.53
Определить абсолютное давление газа в сосуде (рис.2.28), если уровень ртути в вакуумметре h = 358 мм.
Купить задачу 2.53
Задача 2.56
В сообщающиеся сосуды налиты жидкости, имеющие относительные плотности соответственно в левом δ = 1,15, в правом δ = 0,83 (рис. 2.29). Определить разность уровней h2, если абсолютное давление в точке с pc = 128 кПа.
Купить задачу 2.56
Задача 2.60
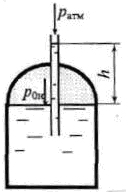
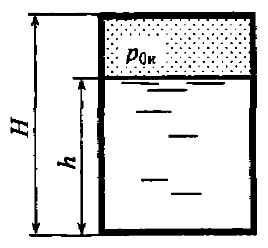
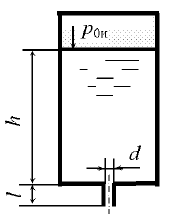
На какую высоту h поднимется бензин в трубке (рис. 2.31), опущенной в бак, если избыточное давление на поверхности бензина в баке p0н = 0,01 МПа. Плотность бензина равна ρб = 720 кг/м3.
Купить задачу 2.60
Задача 3.1
Открытая цистерна диаметром D = 2,2 м заполнена бензином (рис. 3.8), плотность которого ρб = 720 кг/м3. Уровень бензина от дна h = 2,4 м. Определить силу гидростатического давления бензина на торцевую стенку и положение центра давления.
Задача 3.4
На щите (рис. 3.11), наклоненном к горизонту на угол α = 60°, имеется отверстие, которое перекрывается круглой крышкой диаметром d = 0,8 м. Определить силу гидростатического давления и центр давления воды на крышку люка, а = 1,0 м.
Купить задачу 3.4
Задача 3.5
Определить силу гидростатического давления жидкости на круглую крышку колодца диаметром D = 1,2 м (рис. 3.12). Относительная плотность жидкости δ = 1,25, глубины Н1 = 4,5 м, Н2 = 1,0 м.
Купить задачу 3.5
Задача 3.12
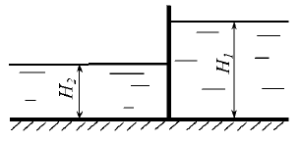
Определить равнодействующую силу и центр давления воды на прямоугольную стенку шириной b = 10 м (рис. 3.19), если глубины воды Н1 = 5 м, Н2 = 3 м.
Купить задачу 3.12
Задача 3.14
Определить равнодействующую силу гидростатического давления воды на прямоугольный затвор высотой h = 1,6 м и шириной b = 2,0 м (рис. 3.21), если глубины воды Н1 = 3,0 м, Н2 = 0,8 м. Найти глубину погружения центра давления.
Задача 3.16
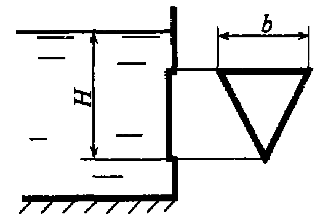
В вертикальной стенке (рис. 3.23) имеется отверстие, перекрываемое щитом в виде равностороннего треугольника, сторона которого b = 2,5 м. Определить силу гидростатического давления воды и положение центра давления, если H = 3,4 м.
Купить задачу 3.16
Задача 3.23
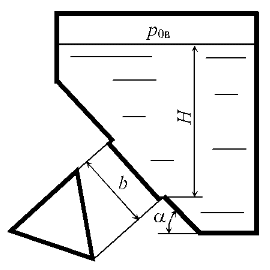
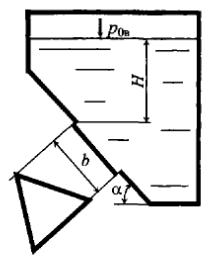
В наклонной стенке резервуара имеется треугольное отверстие, которое перекрывается щитом в форме равностороннего треугольника, высота которого b = 2,5 м (рис. 3.30). Определить силу гидростатического давления воды на щит и глубину погружения центра давления, если Н = 3,1 м, угол наклона щита к горизонту α = 60°, а вакуумметрическое давление в резервуаре р0в = 0,5 · 105 Па.
Купить задачу 3.23
Задача 3.24
Цистерна диаметром D = 2,2 м заполнена бензином (рис. 3.31), плотность которого ρб = 720 кг/м3, и герметично закрыта. Уровень бензина от дна h = 2,4 м. Давление паров бензина на свободной поверхности p0и = 0,08 · 105 Па. Определить силу гидростатического давления бензина на торцевую стенку и положение центра давления.
Купить задачу 3.24
Задача 3.25
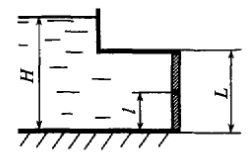
Прямоугольный поворотный затвор размерами L x B = 2 x 3 м перекрывает выход воды из резервуара, глубина в котором H = 5 м (рис. 3.32).
Определить, на каком расстоянии l следует расположить его ось поворота, чтобы для его открытия преодолеть только момент трения.
Купить задачу 3.25
Задача 3.31
На боковой стенке резервуара (рис. 3.38), наклоненной к горизонту на угол α = 60°, имеется люк, который перекрывается круглой крышкой диаметром d = 0,8 м. Определить силу гидростатического давления и центр давления воды на крышку люка, если а = 1,0 м, избыточное давление в резервуаре p0и = 8 кПа.
Купить задачу 3.31
Задача 3.33
В боковой вертикальной стенке резервуара имеется отверстие, перекрываемое треугольным равносторонним щитом, сторона которого b = 1,5 м (рис. 3.40). Определить силу гидростатического давления воды и положение центра давления, если Н = 2,3 м, избыточное давление в резервуаре р0и = 5 кПа.
Купить задачу 3.33
Задача 3.34
Прямоугольное отверстие высотой h = 0,4 м и шириной b = 1,0 м в вертикальной стенке резервуара с водой закрыто щитом (рис. 3.41). Определить силу и центр давления воды на щит, если Н = 0,5 м, вакуумметрическое давление в резервуаре р0в = 5 кПа.
Купить задачу 3.34
Задача 3.36
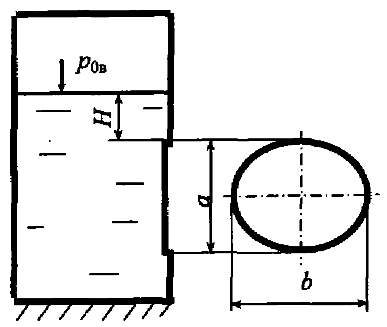
В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса размерами а = 1,5 м, b = 2,5 м (рис. 3.43). Определить силу гидростатического давления воды на щит и положение центра давления, если Н = 0,3 м, вакуумметрическое давление в резервуаре р0в = 20 кПа.
Купить задачу 3.36
Задача 3.37
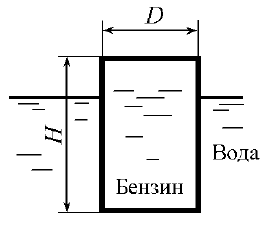
В воде плавает герметично закрытая бочка (рис. 3.44). Определить результирующую силу давления на дно бочки, если давление в ней р0в = 0,1 · 105 Па, плотность бензина ρб = 750 кг/м3, Н = 1,2 м, h = 0,2 м, D = 0,4 м.
Купить задачу 3.37
Задача 3.40
В наклонной стенке резервуара имеется треугольное отверстие, которое перекрывается щитом в форме равностороннего треугольника, высота которого b = 1,8 м (рис. 3.47). Определить силу гидростатического давления жидкости на щит и глубину погружения центра давления, если Н = 0,2 м, угол наклона щита к горизонту α = 60°, а вакуумметрическое давление в резервуаре р0в = 0,5 · 105 Па.
Купить задачу 3.40
Задача 3.41
В закрытый резервуар с вакуумметрическим давлением р0в = 0,05 · 105 Па налит керосин плотностью ρк = 860 кг/м3 (рис. 3.48). Определить силу гидростатического давления и центр давления керосина на круглую крышку лаза диаметром d = 1,0 м. Центр тяжести крышки расположен на глубине Н = 3,0 м.
Купить задачу 3.41
Задача 3.42
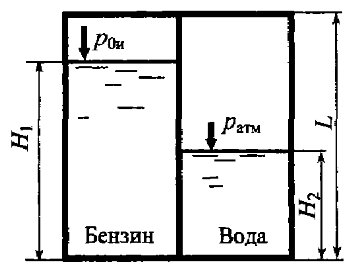
Определить равнодействующую сил давления на перегородку высотой L = 3 м и шириной B = 2 м, если H1 = 2 м, H2 = 1 м (рис. 3.49). Над бензином (ρб = 800 кг/м3) избыточное давление p0и = 0,05 · 105 Н/м2, а над водой – атмосферное давление.
Купить задачу 3.42
Задача 3.43
Определить силу и центр давления на прямоугольную боковую стенку резервуара высотой Н = 3 м и шириной В = 2 м (рис. 3.50). Резервуар герметичен и давление на поверхности нефти (ρн = 900 кг/м3) р0и = 0,1 · 105 Па. Глубина нефти h = 2 м.
Купить задачу 3.43
Задача 3.44
Цистерна диаметром D = 2,2 м заполнена бензином (ρб = 720 кг/м3) до высоты D/2 (рис. 3.51). Определить силу давления на торцевую стенку, если цистерна герметично закрыта и избыточное давление в ней p0и = 0,1 · 105 Па.
Купить задачу 3.44
Задача 3.49
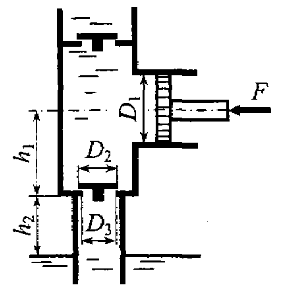
Определить силу (пренебрегая весом клапана), прижимающую всасывающий клапан диаметром D2 = 150 мм к седлу, имеющему диаметр D3 = 100 мм, если диаметр насосного цилиндра D1 = 350 мм, а усилие, действующее на шток, F = 400 Н. Седло клапана расположено ниже оси цилиндра на h1 = 0,5 м и выше свободной поверхности жидкости на h2 = 6,5 м, причем труба над клапаном заполнена водой (рис. 3.56).
Купить задачу 3.49
Задача 3.51
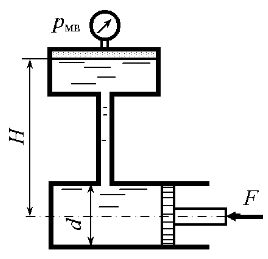
Определить показания мановакуумметра pмв, если к штоку поршня приложена сила F = 0,1 кН. Диаметр поршня d = 100 мм, высота Н = 2,5 м, плотность жидкости ρ = 800 кг/м3 (рис. 3.58).
Купить задачу 3.51
Задача 3.52
Определить абсолютное давление в точке А и вес груза G, лежащего на поршне 2 (рис. 3.59), если для его подъема к поршню 1 приложена сила F = 500 Н. Диаметры поршней D = 300 мм, d = 80 мм. Высота Н = 1,5 м. Плотность масла ρм = 850 кг/м3.
Купить задачу 3.52
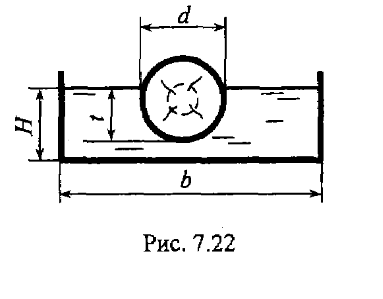
Задача 3.60
При определении гидродинамических характеристик бревно обтекается потоком воды в прямоугольном лотке (рис. 7.22). Определить гидравлический радиус при условии H = 0,5 м, b = 1,0 м, d = 0,2 м, t = 0,16 м.
Купить задачу 3.60
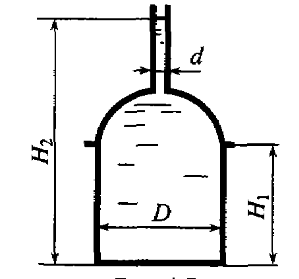
Задача 4.1
Цилиндрический резервуар (рис. 4.7) для хранения мазута диаметром D = 4,0 м имеет полусферическую крышку и сообщается с атмосферой через трубу диаметром d = 0,2 м. Определить вертикальную составляющую силы гидростатического давления мазута на крышку, если Н1 = 4,0 м, Н2 = 8,0 м, плотность мазута ρ = 890 кг/м3.
Купить задачу 4.1
Задача 4.2
Построить тело давления и определить величину и направление силы гидростатического давления воды на полусферическую крышку диаметром d = 1,0 м, Н = 2,0 м (рис. 4.8).
Купить задачу 4.2
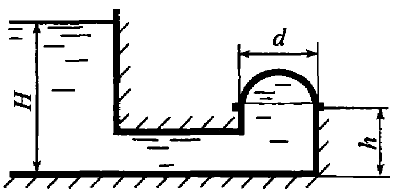
Задача 4.3
Построить тело давления и определить силу, отрывающую полусферическую крышку от основания резервуара (рис. 4.9). Резервуар заполнен водой, диаметр крышки d = 1,2 м, Н = 3,0 м, h = 1,0 м.
Купить задачу 4.3
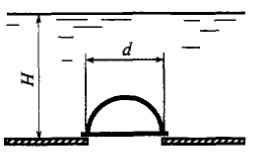
Задача 4.5
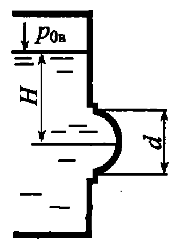
Построить тело давления и определить силу, прижимающую полусферическую крышку диаметром d = 1,2 м к основанию резервуара (рис. 4.11). Резервуар заполнен водой, глубина воды Н = 3,0 м.
Купить задачу 4.5
Задача 4.12
Построить тело давления и определить величину и направление силы давления воды на боковую поверхность секторного затвора радиусом R = 2,0 м и шириной b = 4,0 м (рис. 4.18).
Купить задачу 4.12
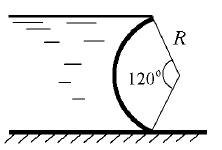
Задача 4.22
Построить тело давления и определить силу давления жидкости P на полусферическую крышку и угол ее наклона к горизонту α (рис. 4.28) при следующих данных: радиус сферы R = 0,6 м, относительная плотность жидкости δ = 0,7, манометрическое давление pм = 8 кПа.
Купить задачу 4.22
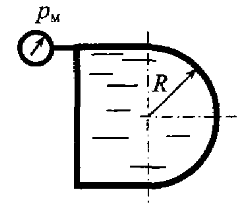
Задача 4.23
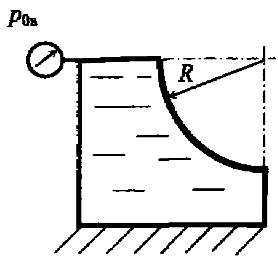
Построить тело давления и определить вертикальную составляющую силы давления жидкости, действующую на полусферическую крышку (рис. 4.29), при следующих данных: радиус сферы R = 2,0 м, плотность жидкости ρ = 1250 кг/м3, манометрическое давление рм = 34 кПа.
Купить задачу 4.23
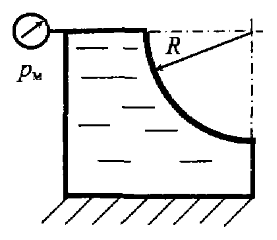
Задача 4.24
Построить тело давления, определить силу давления жидкости Р, действующую на цилиндрическую поверхность, и угол ее наклона к горизонту α (рис. 4.30) при следующих данных: радиус образующей цилиндра R = 1,6 м, длина образующей цилиндра В = 2,5 м, плотность жидкости ρ = 950 кг/м3, манометрическое давление рм = 18 кПа.
Купить задачу 4.24
Задача 4.29
Конический резервуар заполнен жидкостью плотностью ρ = 900 кг/м3. Определить силу давления жидкости, действующую на боковую поверхность резервуара, если D = 2,0 м, d = 1,0 м, H = 1,0 м, H0 = 1,5 м (рис. 4.35), избыточное давление в резервуаре p0и = 0,1 · 105 Па.
Купить задачу 4.29
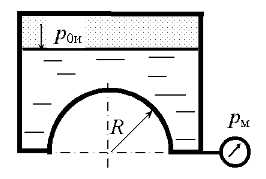
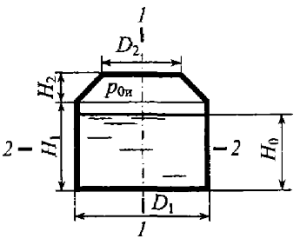
Задача 4.30
Определить горизонтальную и вертикальную составляющие силы гидростатического давления нефти плотностью ρ = 850 кг/м3 на выпуклую торцовую стенку, если D = 3,5 м, H = 2,1 м, а объем выпуклой части (на рис. 4.36 заштрихован) V = 1,5 м3, избыточное давление в резервуаре p0и = 0,05 · 105 Па.
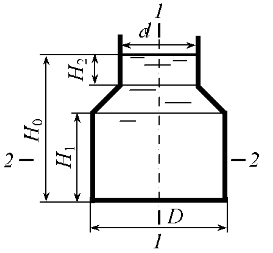
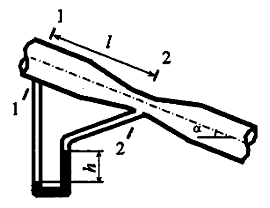
Задача 4.31
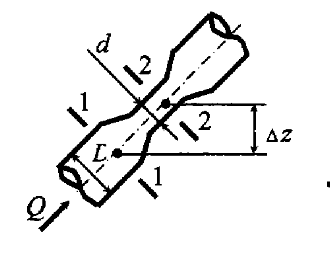
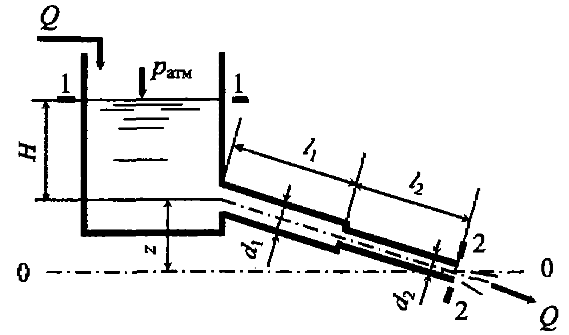
Открытый резервуар (рис. 4.37) заполнен нефтью до уровня H0 = 5,0 м. Определить силы, разрывающие резервуар в плоскостях 1–1 и 2–2, если H1 = 2,0 м, H2 = 1,5 м, плотность нефти ρ = 900 кг/м3.
Купить задачу 4.31
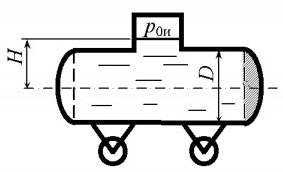
Задача 4.32
Закрытый резервуар (рис. 4.38) заполнен нефтью до высоты H0 = 2,0 м. Определить силы, разрывающие резервуар в плоскостях 1–1 и 2–2, если H1 = 3,0 м; H2 = 1,0 м; D1 = 5,0 м; D2 = 4,0 м; плотность нефти ρ = 900 кг/м3; p0и = 10 кПа.
Купить задачу 4.32
Задача 4.33
Построить тело давления и определить силу, отрывающую полусферическую крышку диаметром d = 1,2 м от основания резервуара (рис. 4.39). Резервуар заполнен водой, глубина воды Н = 2,5 м. Избыточное давление р0и = 5 кПа.
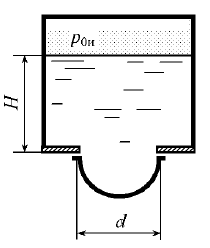
Купить задачу 4.33
Задача 4.34
Определить величину и направление силы давления воды на боковую поверхность цилиндрического затвора диаметром d = 1,6 м и длиной l = 4,0 м (рис. 4.40), если H1 = 3,0 м; H2 = d/2.
Купить задачу 4.34
Задача 4.35
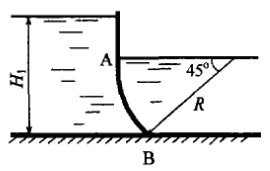
Построить тело давления и определить величину и направление силы гидростатического давления воды, действующую на боковую поверхность секторного затвора АВ с углом сектора 45° (рис. 4.41). Радиус затвора R = 3,0 м, а ширина b = 4,0 м. Уровень воды H1 = 4,0 м.
Купить задачу 4.35
Задача 4.36
Построить тело давления и определить силу давления жидкости Р на полусферическую крышку и угол ее наклона к горизонту α (рис. 4.42) при следующих данных: радиус образующей сферы R = 1,8 м; плотность жидкости ρ = 750 кг/м3; вакуумметрическое давление рв = 40 кПа.
Купить задачу 4.36
Задача 4.37
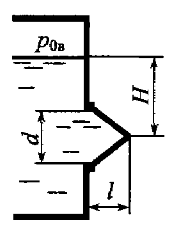
Определить вертикальную и горизонтальную составляющие силы давления воды, действующие на коническую крышку (рис. 4.43), если вакуумметрическое давление в резервуаре р0в = 0,7 · 105 Па, d = 1,2 м, Н = 3,0 м, l = 1,0 м.
Купить задачу 4.37
Задача 4.41
Построить тело давления и определить силу, действующую на полусферическую крышку (рис. 4.46). Резервуар заполнен водой, диаметр крышки D = 1,2 м, Н = 3,0 м, h = 1,0 м. Вакуумметрическое давление в резервуаре р0в = 5 кПа.
Задача 4.49
Построить тело давления и определить силу давления жидкости на цилиндрическую поверхность резервуара (рис. 4.51) м угол ее наклона к горизонту α при следующих данных: радиус образующей цилиндра R = 2,4 м, длина образующей цилиндра b = 1,5 м, относительная плотность жидкости δ = 1,26. Вакуумметрическое давление в резервуаре р0в = 0,45 · 105 Па.
Задача 4.51
Построить тело давления и определить силу давления жидкости на цилиндрическую поверхность резервуара (рис. 4.52) и угол ее наклона к горизонту α при следующих данных: радиус образующей цилиндра R = 1,5 м, длина образующей цилиндра b = 0,8 м, относительная плотность жидкости δ = 0,95. Вакуумметрическое давление в резервуаре р0в = 0,35 · 105 Па.
Купить задачу 4.51
Задача 4.54
Построить тело давления и определить силу давления жидкости Р, действующую на цилиндрическую поверхность, и угол ее наклона к горизонту α (рис. 4.54) при следующих данных: радиус образующей цилиндра R = 1,2 м, длина образующей цилиндра В = 1,5 м, плотность жидкости ρ = 850 кг/м3, вакуумметрическое давление р0в = 22 кПа.
Купить задачу 4.54
Задача 4.56
Определить, при какой глубине воды Н горизонтальная сила давления на полусферическую крышку равна нулю (рис. 4.48), если вакуумметрическое давление в закрытом резервуаре р0н = 0,2 · 105 Па.
Купить задачу 4.56
Задача 4.57
По нефтепроводу диаметром D = 1000 мм перекачивается нефть под избыточным давление ри = 4,0 МПа. Определить силу, разрывающую нефтепровод.
Купить задачу 4.57
Задач, которых нет на странице, Вы можете заказать
Задача 5.5
Прямоугольный понтон шириной В = 2,5 м, длиной L = 6,0 м имеет осадку Т = 0,9 м, причём центр тяжести расположен на высоте hцт = 1,2 м на плоскостью дна. Определить вес груза и проверить остойчивость понтона, если понтон без нагрузки имеет осадку Т0 = 0,1 м.
Купить задачу 5.5
Задача 5.11
Проверить остойчивость понтона длиной L = 50 м, шириной В = 3 м и высотой Н = 1,0 м. Масса понтона с грузом m = 1,2 · 105 кг. Центр тяжести понтона с грузом расположен в центре поперечного сечения.
Купить задачу 5.11
Задача 5.12
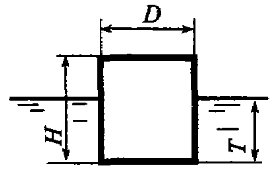
Определить осадку Т и проверить остойчивость бруса, плавающего в воде, в положении указанном на рис. 5.6. Размеры бруса: H = 0,4 м, В = 0,2 м, L = 6,0 м, плотность древесины ρдр = 800 кг/м3, а плотность воды ρ = 1000 кг/м3.
Купить задачу 5.12
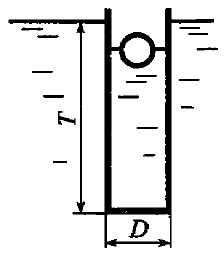
Задача 5.16
Шарообразный поплавок плавает в жидкости, находящейся в цилиндрическом сосуде (рис. 5.7). Сосуд плавает в воде. Вес сосуда G1 = 20 Н, вес жидкости G2 = 50 Н, Т = 1 м, диаметр сосуда D = 0,1 м. Определить вес поплавка.
Купить задачу 5.16
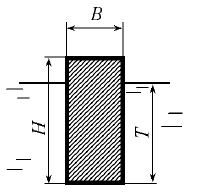
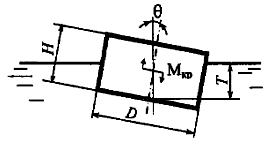
Задача 5.17
Определить угол крена θ деревянного цилиндра (рис. 5.8) с удельным весом γ = 7,5 кН/м3, если на него действует кренящий момент Мкр = 150 Н · м. Диаметр цилиндра D = 1,4 м, высота цилиндра Н = 0,9 м.
Купить задачу 5.17
Задача 5.21
Прямоугольный понтон шириной В = 2,5 м, длиной L = 16 м имеет осадку Т = 0,9 м, причем центр тяжести расположен на высоте h = 1,2 м от плоскости дна. Определить вес груза и проверить остойчивость понтона, если понтон без загрузки имеет осадку t = 0,1 м.
Купить задачу 5.21
Задача 5.22
В воде плавает деревянный цилиндр высотой H и диаметром D = 0,5 м так, что его образующая вертикальна. Определить предельную высоту цилиндра, при которой он теряет остойчивость, если плотность древесины ρдр = 700 кг/м3.
Купить задачу 5.22
Задача 5.23
Понтон прямоугольного сечения (рис. 5.11) массой 4 т имеет следующие размеры: длину L = 10 м, ширину В = 3 м, высоту Н = 1,5 м. Определить грузоподъемность понтона при запасе по высоте борта h = 40 см, а также метацентрический радиус.
Купить задачу 5.23
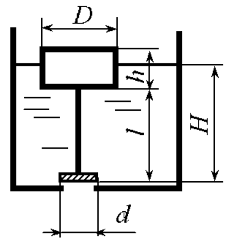
Задача 5.31
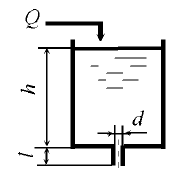
Определить вес поплавка D = 20 см, который при слое бензина H ≥ 80 см обеспечивал бы автоматическое открывание клапана диаметром d = 4 см. Длина тяги l = 74 см. Масса клапана и тяги 0,173 кг. Плотность бензина ρб = 750 кг/м3 (рис. 5.18).
Купить задачу 5.31
Задача 5.32
При каком уровне воды в резервуаре клапан диаметром d = 100 мм откроется (рис. 5.18)? Клапан снабжен поплавковым диаметром D = 20 см и высотой h = 500 мм. Длина тяги l = 1000 мм. Масса поплавка с клапаном и тягой 3,1 кг. Объем клапана и тяги 380 см3.
Купить задачу 5.32
Задача 5.34
Бочка (рис. 5.20), диаметр и высота которой соответственно равны D = 0,50 м, Н = 1,05 м, плавает в воде. Проверить бочку на остойчивость, если в бочке находится 200 л бензина, плотность которого ρб = 750 кг/м3. Масса пустой бочки m = 20 кг.
Купить задачу 5.34
Задача 5.42
Масса стального каната в воздухе m = 2,91 кг/м. Определить вес каната в воде, если плотность воды ρв = 1020 кг/м3, а плотность стали ρст = 7850 кг/м3.
Задача 5.44
Для измерения поверхностной скорости течения изготавливают поплавки из бревна диаметром D = 20 см (рис. 5.27). Определить высоту поплавка при условии: осадка поплавка Т = 3 см, плотность древесины ρдр = 600 кг/м3.
Купить задачу 5.44
Задача 5.45
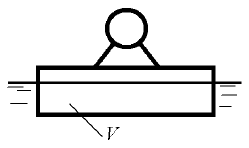
Объем древесины в наплавной опоре V = 20 м3 (рис. 5.28). На опоре установлена лебедка массой 1500 кг. Определить запас плавучести опоры, если плотность древесины ρдр = 800 кг/м3. Опора плавает в пресной воде.
Купить задачу 5.45
Задача 6.3
Призматический сосуд шириной b = 1 м, перемещающийся горизонтально с постоянным ускорением а = 0,2g, разделен плоской перегородкой на два отсека, заполненных водой до высот h1 = 1 м и h2 = 1,75 м (рис. 6.18). Определить суммарную силу давления Р воды на перегородку, если l1 = 2 м, l2 = 1 м.
Купить задачу 6.3
Задача 6.12
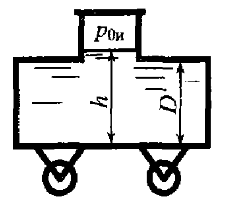
Определить расположение центра тяжести С бетонного раствора (hс и lс), залитого в закрытый кузов автомобиля, при его движении со скоростью υ = 36 км/ч по горизонтальному закруглению радиусом R = 25 м (рис. 6.27). Считать, что кузов имеет форму параллелепипеда: b = 1,8 м, Н = 1,2 м и h = 1,0 м.
Купить задачу 6.12
Задача 6.13
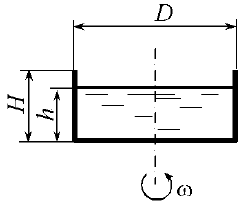
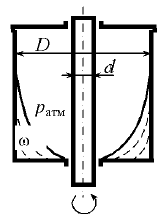
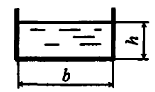
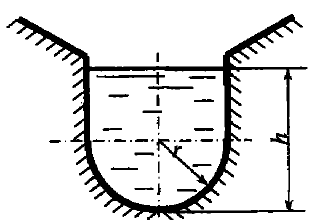
В сосуд высотой Н = 0,3 м залита жидкость до уровня h = 0,2 м. Определить, до какой угловой скорости можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него, если диаметр D = 100 мм (рис. 6.28).
Купить задачу 6.13
Задача 6.21
Цилиндрической сосуд диаметром D = 90 мм вращается на вертикальном валу диаметром d = 20 мм (ри. 6.36). Определить минимальную угловую скорость ω, при которой жидкость не соприкасается с валом, если первоначально сосуд был заполнен до уровня h = 0,06 м. Считать, что жидкость не поднимается до крышки сосуда.
Задача 6.34
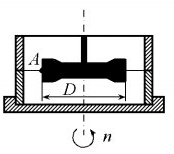
В форму для отливки колеса залит расплавленный чугун (ρ = 7000 кг/м3). Определить, на сколько увеличится давление чугуна в точке А при вращении формы с частотой n = 500 об/мин, если диаметр колеса D = 1000 мм (рис. 6.42).
Купить задачу 6.34
Задача 6.45
Замкнутый цилиндрический сосуд длиной L = 2 м, радиусом R = 0,5 м используется как форма для отливки центробежным способом чугунных труб со средней толщиной стенок δ = 10 мм. Какой должна быть угловая скорость вращения цилиндра с вертикальной осью, если допустимое отклонение толщины стенок от среднего значения составляет Δδ = ±1 мм? Плотность чугуна ρ = 7000 кг/м3.
Купить задачу 6.45
Задача 7.1
Вода движется в прямоугольном лотке с глубиной наполнения h = 0,5 м (рис. 7.7). Ширина лотка b = 1,0 м. Определить, при каком максимальном расходе Q сохранится ламинарный режим, если температура воды t = 30 °С.
Купить задачу 7.1
Задача 7.2
Найти максимальный диаметр d напорного трубопровода, при котором нефть будет двигаться при турбулентном режиме (рис. 7.4), если кинематический коэффициент вязкости нефти ν = 0,30 см2/с, а расход в трубопроводе Q = 8 л/с.
Купить задачу 7.2
Задача 7.3
По конической сходящейся трубе движется бензин. Определить, в сечении с каким диаметром произойдет смена режимов движения, если расход Q = 0,2 л/с, плотность ρ = 750 кг/м3, динамический коэффициент вязкости μ = 6,5·10-4 Па · с.
Купить задачу 7.3
Задача 7.4
Вода движется в треугольном лотке с расходом Q = 30 л/с (рис. 7.8). Ширина потока b = 0,7 м, глубина наполнения лотка h = 0,5 м, температура воды t = 15 °С. Определить режим движения жидкости. Произойдет ли смена режимов движения, если температура воды повысится до t = 50 °С?
Купить задачу 7.4
Задача 7.7
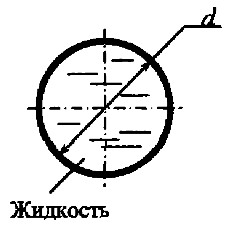
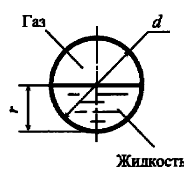
Определить число Рейнольдса по гидравлическому радиусу ReR при безнапорном движении нефти по трубопроводу (рис. 7.9). Трубопровод заполнен нефтью наполовину сечения. Диаметр трубопровода d = 0,5 м, расход Q = 1,2 м3/мин, динамический коэффициент вязкости нефти μ = 0,0027 Па · с, плотность ρ = 900 кг/м3.
Купить задачу 7.7
Задача 7.9
Определить, изменится ли режим движения воды в напорном трубопроводе диаметром d = 0,5 м при возрастании температуры воды от 15 до 65 °С, если расход в трубопроводе Q = 15 л/мин (рис. 7.4).
Купить задачу 7.9
Задача 7.10
Жидкость движется в прямоугольном лотке с расходом Q = 0,1 л/с (рис. 7.7). Ширина лотка b = 1,0 м, глубина наполнения h = 0,3 м. Определить, при какой температуре будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости жидкости от температуры показан на рис. 7.5.
Задача 7.11
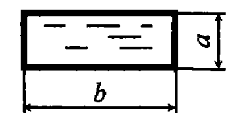
Вода движется под напором в трубопроводе прямоугольного сечения (а × b). Определить, при каком максимальном расходе сохранится ламинарный режим, если температура воды t = 30 °С, а = 0,2 м, b = 0,3 м (рис. 7.11).
Купить задачу 7.11
Задача 7.12
Жидкость движется в треугольном лотке с глубиной наполнения h = 0,5 м (рис. 7.8). Ширина лотка по верху b = 0,1 м. Определить, при каком максимальном расходе Q сохранится ламинарный режим, если кинематический коэффициент вязкости жидкости ν = 10 сСт.
Купить задачу 7.12
Задача 7.13
Найти минимальный диаметр d безнапорного трубопровода, при котором нефть будет двигаться при ламинарном режиме. Трубопровод заполнен нефтью наполовину сечения (рис. 7.9). Кинематический коэффициент вязкости нефти v = 0,22 см2/с, расход нефти в трубопроводе Q = 5 л/с.
Купить задачу 7.13
Задача 7.16
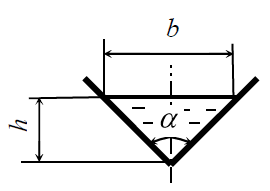
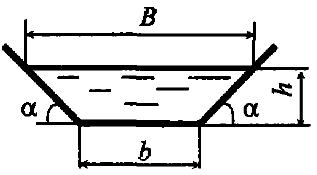
Жидкость движется в трапецеидальном лотке (трапеция равнобокая с расходом Q = 0,01 л/с (рис. 7.10). Ширина лотка по дну b = 0,4 м, глубина наполнения h = 0,2 м, угол наклона боковых стенок лотка к горизонту α = 45°. Динамический коэффициент вязкости жидкости μ = 0,002 Па · с, ее плотность ρ = 800 кг/м3. Определить число Рейнольдса и режим движения жидкости.
Купить задачу 7.16
Задача 7.17
Определить критическую скорость, при которой будет происходить смена режимов движения воды в лотке, имеющем прямоугольную форму поперечного сечения (рис. 7.7). Ширина лотка b = 0,3 м, глубина наполнения h = 0,2 м, температура воды t = 20 °С.
Купить задачу 7.17
Задача 7.19
Жидкость движется в безнапорном трубопроводе (рис. 7.9) с расходом Q = 22 м3/ч. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 80 мм. Определить, при какой температуре будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости жидкости от температуры показан на рис. 7.5.
Купить задачу 7.19
Задача 7.21
По круглому напорному трубопроводу диаметром d = 0,2 м движется нефть (рис. 7.4) со скоростью υ = 0,8 м/с. Определить число Рейнольдса и режим движения нефти, если ее плотность ρ = 850 кг/м3, а динамический коэффициент вязкости μ = 0,0026 Па · с.
Купить задачу 7.21
Задача 7.22
Жидкость движется в безнапорном трубопроводе (рис. 7.9) с температурой t = 30 °C. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 50 мм. Определить, при какой скорости будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости жидкости от температуры показан на рис. 7.5.
Купить задачу 7.22
Задача 7.23
Определить критическую скорость, при которой будет происходить смена режимов движения жидкости в лотке (рис. 7.10), имеющем трапецеидальную форму поперечного сечения (трапеция равнобокая). Глубина наполнения h = 0,3 м, ширина потока по верху В = 1,0 м, ширина по дну b = 0,4 м, кинематический коэффициент вязкости ν = 5 мм2/с.
Купить задачу 7.2.3
Задача 7.34
Для осветления сточных вод используют горизонтальный отстойник, представляющий собой удлиненный прямоугольный в плане резервуар. Глубина h = 2,6 м, ширина b = 5,9 м. Температура воды 20°С. Определить среднюю скорость и режим движения сточной жидкости, если ее расход Q = 0,08 м3/с, а коэффициент кинематической вязкости ν = 1,2 · 10-6 м2/с. При какой скорости движения жидкости в отстойнике будет наблюдаться ламинарный режим движения жидкости?
Купить задачу 7.34
Задача 7.45
Определить гидравлический радиус живого сечения напорного потока, протекающего через щель. Форма потока изображена на рис. 7.16.
Купить задачу 7.45
Задача 7.53
Радиатор системы охлаждения двигателя внутреннего сгорания состоит из пучка трубок диаметром 8 мм, по которым протекает вода при температуре t = 90 °С. Определить минимальную допустимую среднюю скорость движения воды в трубках при условии, что режим движения должен быть турбулентным.
Купить задачу 7.53
Задача 8.1
Вода движется в трубчатом расходомере в направлении от сечения 1–1 к сечению 2–2 (рис. 8.4). Манометрическое давление в сечении 1–1 больше давления в сечении 2–2 на Δp = 25 кПа. Определить расход Q, если внутренний диаметр трубопровода в сечении 1–1 D = 65 мм, а в сечении 2–2 d = 40 мм, разность отметок сечений Δz = 2 м. Потерями напора пренебречь.
Купить задачу 8.1
Задача 8.10
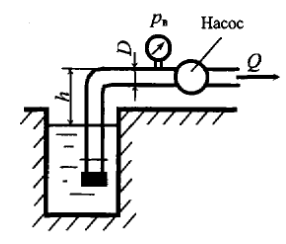
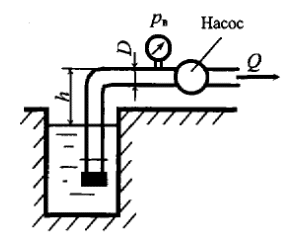
Насос с подачей Q = 7,2 м3/ч забирает воду из колодца (рис. 8.9). Определить наибольший вакуум рвак при входе в насос. Внутренний диаметр трубопровода D = 80 мм, высота установки насоса над уровнем жидкости h = 4 м. Потери напора Δh = 0,5 м.
Купить задачу 8.10
Задача 8.12
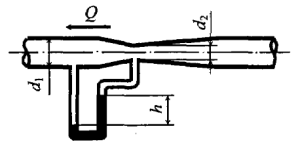
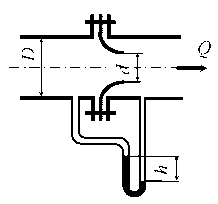
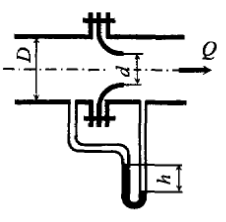
По горизонтальному трубопроводу переменного сечения движется нефть (рис. 8.7), плотность которой ρн = 850 кг/м3. Диаметр в узком сечении трубопровода d2 = 50 мм. Расход нефти в трубопроводе Q = 0,5 л/с, разность уровней в дифференциальном манометре, заполненном ртутью плотностью ρрт = 13600 кг/м3, составляет h = 35 мм. Определить диаметр трубопровода в широком сечении. Потерями напора пренебречь.
Купить задачу 8.12
Задача 8.13
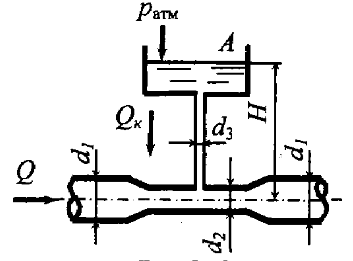
По горизонтальному трубопроводу переменного сечения движется вода (рис. 8.10). Из бачка А по трубке, подведенной к трубопроводу, поступает краситель, имеющий плотность ρ = 1300 кг/м3. Определить расход воды в трубопроводе, при котором прекратится подача красителя. Уровень красителя в бачке H = 0,5 м, диаметр трубопровода в широком сечении D = 150 мм, в узком d = 100 мм, манометрическое давление воды в широком сечении трубопровода равно 30 кПа. Потерями напора пренебречь.
Купить задачу 8.13
Задача 8.15
Насос с подачей Q = 7 л/с забирает воду из колодца (рис. 8.9). Внутренний диаметр трубопровода D = 80 мм. Определить высоту установки насоса над уровнем жидкости h, чтобы вакуум при входе в насос не превышал рв = 50 кПа. Потери напора hw = 0,6 м.
Купить задачу 8.15
Задача 8.17
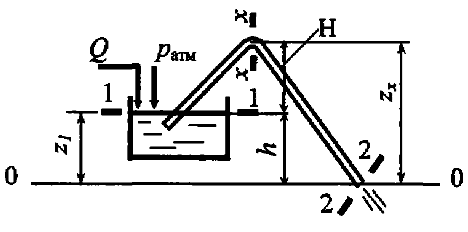
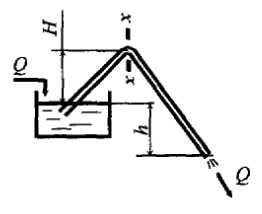
Определить, на какую теоретическую высоту Н относительно уровня жидкости в питающем резервуаре можно поднять сечение х–х сифонного трубопровода (рис. 8.3), чтобы вакуумметрическое давление р в этом сечении не превышало 40 кПа. Средняя скорость движения жидкости в трубопроводе υ = 1,8 м/с, плотность жидкости ρ = 900 кг/м3. Потерями напора пренебречь.
Купить задачу 8.17
Задача 8.22
По горизонтальному трубопроводу переменного сечения движется вода (рис. 8.10). Из бачка А по трубке, подведенной к трубопроводу, поступает краситель плотностью ρ = 1250 кг/м3. Определить, при какой высоте H прекратится подача красителя. Расход воды в трубопроводе Q = 1,8 м3/мин, диаметр трубопровода в широком сечении d1 = 200 мм, в узком d2 = 100 мм, абсолютное давление воды в трубопроводе с диаметром d1, p1 = 150 кПа. Потерями напора пренебречь.
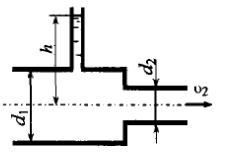
Задача 8.23
По горизонтальному трубопроводу переменного сечения с диаметрами d1 = 50 мм и d2 = 30 мм движется нефть (рис. 8.7) с расходом Q = 1,1 м3/сут. Определить, пренебрегая потерями напора, разность давлений в узком и широком сечениях трубопровода.
Купить задачу 8.23
Задача 8.24
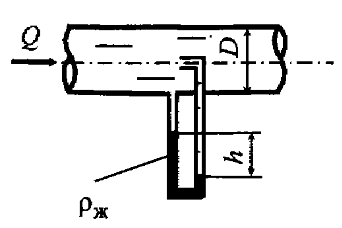
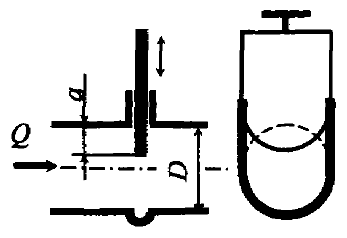
По трубопроводу диаметром D = 150 мм движется вода с расходом 20 л/мин. Определить, пренебрегая потерями напора, разность уровней в жидкостном манометре (рис. 8.6). Плотность жидкости в манометре ρж = 1,3 г/см3.
Купить задачу 8.24
Задача 8.25
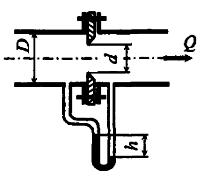
Определить, пренебрегая потерями напора, расход воды в трубопроводе диаметром D = 10 см (рис. 8.5), если разность уровней жидкости в манометре h = 250 мм. Плотность жидкости в манометре ρж = 1250 кг/м3.
Купить задачу 8.25
Задача 8.29
По горизонтальному трубопроводу переменного сечения движется жидкость (рис. 8.7), плотность которой ρж = 1200 кг/м3. Диаметр в широком сечении трубопровода d1 = 100 мм, а в узком d2 = 75 мм, разность уровней в дифференциальном манометре, заполненном ртутью с плотностью ρрт = 13600 кг/м3, составляет h = 25 см. Определить скорость в широком сечении трубопровода. Потерями напора пренебречь.
Купить задачу 8.29
Задача 8.31
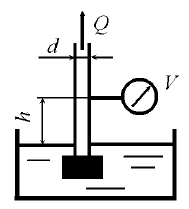
Определить, на какую высоту h поднимается вода в трубке, один конец которой присоединен к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе Q = 0,025 м3/с, избыточное давление р1 = 49 · 103 Па, диаметры d1 = 100 мм, d2 = 50 мм (рис. 8.12). Потери напора не учитывать.
Купить задачу 8.31
Задача 8.32
Определить диаметр суженной части трубопровода d2, если вода в трубке поднимается на высоту h = 3,5 м при расходе воды в трубопроводе Q = 0,007 м3/с и диаметре d1 = 0,10 м. Абсолютное давление в сечении трубопровода диаметром d1, р1 = 1,5 · 105 Па (рис. 8.12). Потери напора не учитывать.
Купить задачу 8.31
Задача 8.34
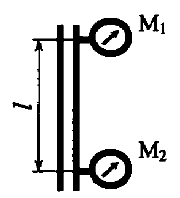
На вертикальной водопроводной трубе постоянного диаметра на расстоянии l = 10 м установлены два манометра. Нижний манометр М2 показывает давление 1,2 кг/см2, а верхний М1 – 0,8 кг/см2. Определить гидравлический уклон и направление движения жидкости (рис. 8.13).
Купить задачу 8.34
Задача 8.36
По нагнетательному патрубку диаметром d1 = 200 мм вентилятором подается воздух (ρ = 1,2 кг/м3) с расходом Q = 0,8 м3/с при избыточном давлении р1 = 1,0 кПа. К патрубку подсоединен диффузор с диаметром выходного сечения d2 = 300 мм. Определить давление воздуха на выходе из диффузора. Изменение плотности воздуха и потери в диффузоре не учитывать (рис. 8.15).
Купить задачу 8.36
Задача 8.37
Определить расход воды через водомер Вентури, установленный под углом α = 30° к горизонту, если показание дифференциального ртутного манометра h = 600 мм рт. ст. (рис. 8.16). Диаметры водомера в сечениях 1–1 и 2–2 соответственно равны d1 = 200 мм и d2 = 75 мм, расстояние между сечениями l = 400 мм. Потерями пренебречь.
Купить задачу 8.37
Задача 8.41
В закрытом резервуаре поддерживается при постоянном уровне постоянное избыточное давление р0н = 0,5 · 105 Па, под воздействием которого вода при температуре t = 50 °С поступает по трубе диаметром d = 50 мм на высоту h = 3,0 м (рис. 8.19). Потери напора в трубе hw = 1,5 м. Определить расход воды в трубе, если на выходе из трубы давление атмосферное. Изменением плотности воды при изменении давления пренебречь.
Купить задачу 8.41
Задача 8.42
По трубопроводу диаметром d = 100 мм вода падает в закрытый бак с избыточным давление р0и = 0,2 · 105 Па. Определить расход воды Q, если глубина воды в баке h = 3 м; показания манометра pм = 1,0 · 105 Па. Потери напора в трубке hw = 4,2 м (рис. 8.20).
Купить задачу 8.42
Задача 8.43
Из закрытого бака вода при температуре 4 °С поступает по трубе d = 100 мм на высоту h = 5 м (рис. 8.19). Расход воды Q = 0,02 м3/с, потери напора hw = 4,2 м. Определить давление р0и на поверхности воды в баке.
Купить задачу 8.43
Задача 8.49
Вентилятором воздух плотностью ρ = 1,2 кг/м3 подается в помещение по всасывающей трубе диаметром D = 200 мм. Определить вакуумметрическое давление рв перед вентилятором, если его производительность Q = 1300 м3/ч (рис. 8.23). Потерями во всасывающей трубе пренебречь.
Задача 8.50
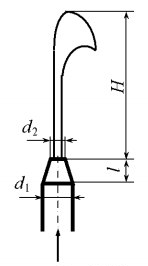
Струя из брандспойта бьет на высоту H = 15 м (рис. 8.17). Определить давление на входе в брандспойт и расход воды при следующих исходных данных: диаметр входного сечения d1 = 70 мм, диаметр выходного сечения d2 = 25 мм, длина брандспойта l = 600 мм, потери напора в брандспойте hw = 0,35 м.
Задача 8.51
На вертикальной водопроводной трубе, состоящей из труб диаметром d1 = 27 мм и d2 = 15 мм, установлены два манометра. Нижний манометр М2 показывает давление 1,6 кг/см2, а верхний – М1 = 1,2 кг/см2. Определить направление движения воды, гидравлический и пьезометрический уклоны, если расход Q = 0,3 л/с (рис. 8.24).
Купить задачу 8.51
Задача 8.54
Трубопровод диаметром d1 = 100 мм заканчивается коротким отрезком трубопровода диаметром d2 = 20 мм, из которого вода вытекает в атмосферу со скоростью υ2 = 4,0 м/с (рис. 8.26). Определить показание пьезометра h, если потери напора hw = 1,0 м.
Купить задачу 8.54
Задача 8.55
Трубопровод диаметром d1 =50 мм заканчивается коротким отрезком трубопровода d2 = 100 мм, из которого вода вытекает в атмосферу со скоростью υ2 = 1 м/с (рис. 8.27). Определить вакуумметрическое давление рв, если потери напора hw = 0,15 м.
Купить задачу 8.55
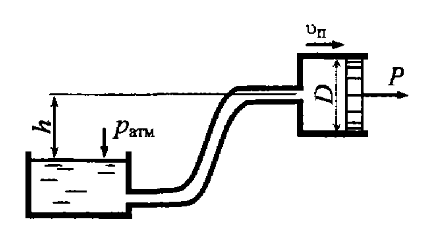
Задача 8.60
Поршень диаметром D = 60 мм, двигаясь равномерно со скоростью Vп = 0,1 м/с, всасывает керосин (ρк = 850 кг/м3) из открытого бака (рис. 8.32). Определить усилие на поршне, если высота всасывания h = 3 м, потери напора в трубопроводе hw = 1,2 м. Трением поршня в цилиндре пренебречь.
Купить задачу 8.60
Задача 9.1
Горизонтальная труба (рис. 9.8) диаметром d = 100 мм состоит из двух участков и соединяет резервуары, в которых поддерживаются постоянные уровни H1 = 6 м и H2 = 2 м, длина каждого участка трубопровода l = 25 м. Определить расход воды, если коэффициент гидравлического трения λ = 0,025.
Купить задачу 9.1
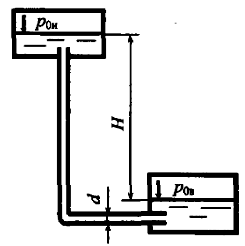
Задача 9.2
По трубопроводу (рис. 9.9), соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает жидкость плотностью ρ = 1250 кг/м3. Диаметр трубопровода d = 20 мм. В верхнем баке поддерживается избыточное давление р0и = 15 кПа, а в нижнем – вакуумметрическое давление р0в = 7 кПа. Разность уровней в баках Н = 5 м. Определить расход жидкости, если коэффициент гидравлического трения λ = 0,028, а длина трубопровода l = 15 м. Местными потерями напора пренебречь.
Купить задачу 9.2
Задача 9.3
Из напорного бака по наклонному трубопроводу переменного сечения (рис. 9.5) движется жидкость относительной плотностью δ = 0,85. Диаметры участков трубопровода d1 = 50 мм, d2 = 30 мм, а длина соответственно равна l1 = 80 м, l2 = 40 м. Начало трубопровода расположено выше его конца на величину z = 3,5 м. Для обоих участков трубопровода коэффициент гидравлического трения λ = 0,038. Какой уровень H необходимо поддерживать в напорном баке, чтобы скорость движения жидкости на выходе из трубопровода была υ = 1,8 м/с? Местными потерями напора пренебречь.
Купить задачу 9.3
Задача 9.4
По трубопроводу (рис. 9.10), соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает жидкость плотностью ρ = 850 кг/м3. Диаметр трубопровода d = 50 мм. В верхнем баке создан вакуум р0в = 60 кПа, а в нижнем баке поддерживается манометрическое давление р0и = 35 кПа. Разность уровней в баках Н = 8 м. Определить расход жидкости, если коэффициент гидравлического трения λ = 0,032, а длина трубопровода l = 30 м. Местными потерями напора пренебречь.
Купить задачу 9.4
Задача 9.5
Определить среднюю скорость движения воды в сифонном трубопроводе υ (рис. 9.11). Диаметр трубопровода d = 40 мм, а его длина l = 18 м. Высота расположения уровня жидкости в питающем резервуаре относительно нижней точки трубопровода h = 3,6 м, коэффициент гидравлического трения λ = 0,034. Местными потерями напора пренебречь.
Купить задачу 9.5
Задача 9.9
Горизонтальная труба (рис. 9.6) диаметром d = 75 мм соединяет резервуары, в которых поддерживаются постоянные уровни H1 = 1,5 м, H2 = 0,5 м. Для регулирования расхода на трубопроводе установлен вентиль. Определить расход в трубопроводе, если манометрическое давление в напорном баке pм = 17 кПа, коэффициент сопротивления вентиля ζ = 8,5.
Купить задачу 9.9
Задача 9.12
По горизонтальному трубопроводу переменного сечения (рис. 9.15) движется жидкость относительной плотностью δ = 0,85 с расходом Q = 2,7 м3/ч. Диаметры участков трубопровода d = 25 мм, D = 35 мм.
Определить местные потери напора, если разность уровней в пьезометрах h = 25 мм.
Купить задачу 9.12
Задача 9.13
По трубопроводу (рис. 9.9), соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает жидкость, имеющая относительную плотность δ = 0,75. Диаметр трубопровода d = 5 см. В верхнем баке поддерживается избыточное давление р0и = 24 кПа. Разность уровней в баках Н = 3 м. Определить, какое разрежение (вакуум) необходимо создать в нижнем баке для пропуска расхода по трубопроводу Q = 0,035 м3/с, если коэффициент гидравлического трения λ = 0,031, длина трубопровода l = 23 м, плотность жидкости ρ = 900 кг/м3. Местными потерями напора пренебречь.
Купить задачу 9.13
Задача 9.16
По трубопроводу (рис. 9.10), соединяющему два резервуара, из верхнего резервуара в нижний перетекает вода. В резервуарах поддерживаются постоянные уровни. Диаметр трубопровода d = 45 мм. В верхнем баке создан вакуум рв = 12 кПа. Разность уровней в баках Н = 12 м. Какое избыточное давление необходимо создать в нижнем баке, чтобы скорость жидкости в трубопроводе была υ = 3,8 м/с, если коэффициент гидравлического трения λ = 0,025, а длина трубопровода l = 41 м. Местными потерями напора пренебречь.
Купить задачу 9.16
Задача 9.23
По трубопроводу (рис. 9.9), соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает жидкость, имеющая плотность ρ = 1150 кг/м3. Диаметр трубопровода d = 40 мм. В нижнем баке создан вакуум рв =12 кПа. Разность уровней в баках Н = 1,3 м. Определить, какое давление необходимо создать в верхнем баке для пропуска расхода по трубопроводу Q = 0,035 м3/с, если коэффициент гидравлического трения λ = 0,035, длина трубопровода l = 32 м. Местными потерями напора пренебречь.
Купить задачу 9.23
Задача 9.27
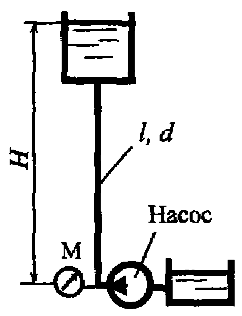
Насос (рис. 9.12) подает воду в водонапорную башню по трубопроводу на высоту Н = 25 м. Показания манометра, установленного в начале участка трубопровода, рм = 3,2 бар. Вода движется по трубопроводу со скоростью υ = 1,8 м/с. Определить коэффициент гидравлического трения, если длина трубопровода l = 23 м, а диаметр d = 4 см. Местными потерями напора пренебречь.
Купить задачу 9.27
Задача 9.33
По горизонтальному трубопроводу длиной l = 430 м и диаметром d = 80 мм движется вода со скоростью υ = 1,8 м/с. Определить, какая скорость будет в трубопроводе, если длину трубопровода уменьшить в 10 раз, а перепад давления в начале и конце трубопровода оставить прежним. Кинематический коэффициент вязкости v = 0,15 см2/с, шероховатость стенок трубопровода Δ = 0,3 мм. Местные потери напора не учитывать.
Купить задачу 9.27
Задача 9.34
Насос всасывает жидкость плотностью ρ = 1050 кг/м3 из резервуара в трубопровод через фильтр с обратным клапаном (рис. 9.17). На всасывающем трубопроводе установлен вакуумметр на высоте h = 0,2 м над уровнем жидкости в резервуаре. Диаметр трубопровода d = 35 мм, показания вакуумметра рв = 12 кПа, скорость жидкости в трубопроводе υ = 1,4 м/с. Определить коэффициент местного сопротивления фильтра с обратным клапаном. Другими потерями напора пренебречь.
Купить задачу 9.34
Задача 9.36
По стальному трубопроводу диаметром d = 5 см и длиной l = 120 м подается вода на высоту Δz = 15 м. На трубопроводе имеются 4 поворота угол 90° с угольником и 2 обыкновенных вентиля. Определить, какой напор должен создавать насос, установленный в начале участка, чтобы скорость воды в трубопроводе стала υ = 1,2 м/с. Температура воды t = 25 °С. Шероховатость стенок трубопровода Δ = 0,1 мм.
Купить задачу 9.36
Задача 9.41
По горизонтальному трубопроводу, на котором установлено сопло движется жидкость плотностью ρ = 800 кг/м3 (рис. 9.18). Перепад давления перед соплом и на выходе из него составляет 20 кПа. Диаметр трубопровода D = 75 мм, а сопла d = 50 мм. Определить расход жидкости, если коэффициент сопротивления сопла ζ = 0,12. Сжатие струи на выходе из сопла отсутствует.
Задача 9.44
По горизонтальному трубопроводу диаметром d = 80 мм и длиной l = 410 м движется жидкость, имеющая относительную плотность δ = 1,15 и динамический коэффициент вязкости μ = 0,0052 Па · с. Определить напор в конце участка трубопровода, если для пропуска расхода Q = 115 л/мин в начале трубопровода создано манометрическое давление рм = 125 кПа, шероховатость трубопровода Δ = 0,1 мм.
Купить задачу 9.44
Задача 9.49
По горизонтальному трубопроводу, на котором установлено сопло (рис. 9.18), движется вода с расходом Q = 1,8 л/с. Диаметр трубопровода D = 50 мм, сопла d = 30 мм. Определить показания ртутного дифференциального манометра, если коэффициент сопротивления сопла ζ = 0,15. Сжатие струи на выходе из сопла отсутствует.
Купить задачу 9.49
Задача 9.51
На участке горизонтального трубопровода диаметром D = 60 мм, по которому движется вода с расходом Q = 8,2 л/с, имеются 4 поворота трубы на угол 90° с угольниками и вентиль. Вентиль полностью открыт и имеет коэффициент сопротивления ζвент = 4,5. При некотором закрытии вентиля расход в трубопроводе уменьшился в два раза. Определить коэффициент сопротивления вентиля, если потери напора остались прежними. Потерями напора по длине пренебречь.
Купить задачу 9.51
Задача 9.52
По горизонтальному трубопроводу переменного сечения движется минеральное масло плотностью ρ = 750 кг/м3, расход Q = 2,3 л/с. Трубопровод имеет внезапное сужение от диаметра d1 = 60 мм до диаметра d2 = 40 мм, вентиль обыкновенный, поворот трубы на 90° с угольником и счетчик расхода жидкости. Определить, какое давление будет в конце участка, если давление в начале участка трубопровода р = 165 кПа. Потерями напора по длине пренебречь.
Купить задачу 9.52
Задача 9.54
На участке горизонтального трубопровода диаметром D = 100 мм, по которому движется вода с расходом Q = 0,041 м3/с, имеется счетчик расхода жидкости, 4 поворота трубы на 90° с угольниками. Манометрическое давление в начале участка трубопровода рм = 350 кПа. Определить, какое манометрическое давление необходимо создать в конце участка для пропуска того же расхода, если на трубопровод установить диафрагму с диаметром d = 25 мм. Потерями напора по длине пренебречь.
Купить задачу 9.54
Задача 9.55
По участке горизонтального трубопровода диаметром D = 120 мм, по которому движется вода с расходом Q = 0,015 м3/с, имеется счетчик расхода жидкости, 4 поворота трубы на 90° (ζпов = 1,3) и задвижка. Задвижка закрыта на три четверти a/D = 0,75 (рис. 9.4). В конце участка установлен манометр, показание которого pм = 45 кПа. Определить какое манометрическое давление необходимо создать в начале участка для пропуска того же расхода, если задвижку поднять до половины диаметра трубопровода. Потерями напора по длине пренебречь.
Купить задачу 9.55
Задача 9.56
По горизонтальному трубопроводу диаметром d = 25 мм и длиной l = 180 м движется вода, имеющая температуру t = 50 °С, со скоростью υ = 2,3 м/с. На трубопроводе имеется 4 поворота на угол 90° с угольниками, счетчик расхода жидкости и обыкновенный вентиль. Шероховатость трубопровода Δ = 0,2 мм. Определить, какая будет скорость при тех же потерях напора, если вентиль прикрыть так, чтобы его коэффициент сопротивления равнялся ζ = 32.
Купить задачу 9.56
Задача 9.57
По горизонтальному трубопроводу, на котором установлена диафрагма (рис. 9.19), движется вода с расходом Q = 8,2 л/с. Диаметр трубопровода D = 80 мм, а диафрагмы d = 35 мм. Определить показания ртутного дифференциального манометра. Сжатием струи на выходе из диафрагмы пренебречь.
Купить задачу 9.57
Задача 9.60
По горизонтальному трубопроводу диаметром d = 50 мм и длиной l = 180 м движется жидкость, имеющая относительную плотность δ = 1,25 и динамический коэффициент вязкости μ = 0,0085 Па · с. Определить необходимый перепад напоров в начале и конце участка трубопровода, если расход Q = 30 л/мин, а шероховатость трубопровода Δ = 0,5 мм.
Купить задачу 9.60
Задача 10.2
Вода вытекает из открытого резервуара через внешний цилиндрический насадок диаметром d = 3,2 см и длиной l = 16 см в атмосферу (рис. 10.9) при h = 55 см. В резервуар поступает вода с расходом Q. Определить глубину воды в резервуаре, если насадок заменить отверстием того же диаметра.
Задача 10.3
Вода вытекает в атмосферу через установленный на боковой поверхности закрытого резервуара насадок диаметром d = 6 см. Избыточное давление на свободной поверхности жидкости р0и = 6,1 кПа, расход жидкости Q = 5 л/с, глубина погружения насадка Н = 90 см. Определить коэффициент расхода насадка.
Купить задачу 10.3
Задача 10.5
Жидкость вытекает из закрытого резервуара в атмосферу через внешний цилиндрический насадок диаметром d = 35 мм и длиной l = 170 мм (рис. 10.10). Избыточное давление на свободной поверхности жидкости p0и = 15 кПа, глубина жидкости в резервуаре h = 0,75 м. Определить расход жидкости через насадок, если ее относительная плотность δ = 0,85.
Купить задачу 10.5
Задача 10.9
Вода вытекает из закрытого резервуара в атмосферу через отверстие диаметром d = 30 мм (рис. 10.7). Избыточное давление на свободной поверхности жидкости p0и = 12 кПа, расход жидкости Q = 3,5 л/с. Определить глубину погружения отверстия.
Купить задачу 10.9
Задача 10.11
Жидкость вытекает из открытого резервуара в атмосферу (рис. 10.5) через малое отверстие в тонкой стенке под напором Н = 0,8 м. Центр отверстия расположен на высоте h = 75 см от пола. Какой напор нужно создать, чтобы дальность полета струи осталась прежней, если центр отверстия расположить относительно пола на высоте h = 90 см.
Купить задачу 10.11
Задача 10.12
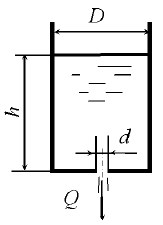
Время частичного опорожнения вертикально расположенного цилиндрического открытого бака через донное отверстие в тонкой стенке составило t = 40 с. За это время уровень жидкости изменился от h1 = 2 м до h2 = 1 м. Определить диаметр отверстия, если диаметр бочки D = 0,5 м (рис. 10.12).
Купить задачу 10.12
Задача 10.14
Жидкость вытекает из закрытого резервуара в атмосферу через отверстие диаметром d = 20 мм (рис. 10.4). Глубина погружения отверстия h = 0,75 м. Какое манометрическое давление необходимо создать на поверхности жидкости для пропуска расхода Q = 1,5 л/с, если плотность жидкости ρ = 800 кг/м3.
Купить задачу 10.14
Задача 10.15
Открытый резервуар с вертикальными стенками опоражнивается через коноидальный насадок диаметром d = 5 см. Определить площадь поперечного сечения резервуара, если напор воды за время t = 2 мин понизился на ΔН = 5 см и стал равным Н = 35 см. Насадок присоединен к отверстию на боковой поверхности резервуара.
Купить задачу 10.15
Задача 10.16
Жидкость вытекает из закрытого резервуара в атмосферу через внешний цилиндрический насадок диаметром d = 40 мм (рис. 10.7). Глубина погружения насадка h = 0,45 м. Какое манометрическое давление необходимо создать на поверхности жидкости для пропуска расхода Q = 7,5 л/с, если плотность жидкости ρ = 850 кг/м3, длина насадка l = 200 мм.
Купить задачу 10.16
Задача 10.17
Жидкость вытекает из открытого резервуара в атмосферу (рис. 10.5) через малое отверстие в тонкой стенке диаметром d = 35 мм с расходом Q = 1,7 л/с. Определить дальность полета струи, если центр отверстия расположен на высоте h = 50 см от пола.
Купить задачу 10.17
Задача 10.21
Открытый резервуар с вертикальными стенками опоражнивается через внешний цилиндрический насадок диаметром d = 2,5 см. Через 35 с напор составил Н = 1,5 м. Определить расход в начальный момент времени, если площадь поперечного сечения резервуара Ω = 1,75 м2. Насадок присоединен к отверстию на боковой стенке резервуара.
Купить задачу 10.21
Задача 10.22
Жидкость вытекает из открытого резервуара через отверстие диаметром d = 30 мм при постоянном напоре h = 0,65 м (рис. 10.9). Определить, с каким диаметром необходимо присоединить коноидальный насадок длиной l = 120 мм для пропуска того же расхода.
Купить задачу 10.22
Задача 10.23
Жидкость вытекает из открытого резервуара в атмосферу (рис. 10.5) через малое отверстие в тонкой стенке диаметром d = 25 мм под напором Н = 0,7 м. Центр отверстия расположен на высоте h = 65 см от пола. На сколько увеличится дальность полета струи, если к отверстию присоединить коноидальный насадок.
Купить задачу 10.23
Задача 10.29
Жидкость вытекает из открытого резервуара в атмосферу (рис. 10.8) через малое отверстие в тонкой стенке диаметром d = 3 см. Дальность полета струи составляет 1 м. Отверстие расположено на высоте h = 0,75 м от пола. Определить расход жидкости через отверстие.
Задача 10.30
Бак с водой опоражнивается через малое отверстие в тонкой стенке (рис. 10.12). Диаметр отверстия d = 1,5 см, а диаметр бочки D = 85 см. Найти расход воды в начальный момент времени, если опорожнение бака произошло за 20 мин.
Задача 10.33
Через отверстие в тонкой боковой стенке вытекает вода под напором Н = 16 м. Изменится ли расход, если к отверстию подсоединить внешний цилиндрический насадок с тем же диаметром?
Купить задачу 10.33
Задача 10.34
Из резервуара происходит истечение воды при переменном напоре через внешний цилиндрический насадок диаметром d = 6 см, установленный на боковой поверхности резервуара. Определить время истечения 10 м3 воды, если площадь поперечного сечения резервуара 5 м2, а начальный напор Н1 = 15 м.
Купить задачу 10.34
Задача 10.36
По короткой трубе диаметром d = 0,10 м из одного резервуара в другой перетекает бензин (ρб = 800 кг/м3). Определить начальный расход, если h1 = 2,0 м; h2 = 0,5 м; избыточное давление в одном резервуаре p0из = 0,2 · 105 Па (рис. 10.13).
Купить задачу 10.36
Задача 10.37
Из закрытого резервуара вода вытекает через отверстие диаметром d0 = 0,02 м и внешний цилиндрический насадок диаметром dн = 0,02 м. Определить избыточное давление в резервуаре, если разность расходов через насадок и отверстие ΔQ = 7 · 10-4 м3/с, а глубина h = 1,5 м (рис. 10.17).
Купить задачу 10.37
Задача 10.38
Определить расход воды Q через отверстие диаметром d = 0,08 м, коэффициент расхода которого μ = 0,65, если показание манометра pм = 150 кПа и высота установки манометра над осью отверстия h = 1,5 м (рис. 10.15).
Купить задачу 10.38
Задача 10.43
Из открытого бака вода вытекает через малое отверстие в атмосферу.
Глубина воды в баке h = 3м поддерживается постоянной. При какой высоте h1 отверстия от пола дальность падения струи l будет максимальной (рис. 10.22)?
Купить задачу 10.43
Задача 10.44
Из открытого бака вода вытекает через два малых отверстия в атмосферу. Глубина воды в баке h = 3 м поддерживается постоянной. При какой высоте h2 расположения второго отверстия дальность струи из него будет такой же, как и из первого отверстия, расположенного на высоте h1 = 1 м от пола (рис. 10.23)?
Купить задачу 10.44
Задача 10.51
Из бака при постоянном напоре вытекает вода через внешний цилиндрический насадок диаметром d = 20 мм. Определить расход, если давление в насадке равно 70 кПа.
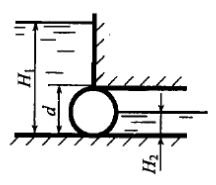
Задача 10.54
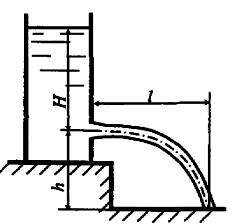
Водоспуск плотины пропускает расход Q = 2 м3/с при перепаде уровней h1 – h2 = 10 м (рис. 10.14). Определить необходимый диаметр водоспуска d и минимальное затопление h2, чтобы вакуум внутри водоспуска был меньше pв = 4 · 104 Па. При решении водоспуск считать как внешний цилиндрический насадок.
Купить задачу 10.54
Задача 11.1
Определить расход воды в трапецеидальном канале (рис. 11.1) при следующих данных: ширина канала по дну b = 2,5 м, глубина наполнения h = 1,1 м, коэффициенты заложения откосов m1 = 2,25, m2 = 1,75, коэффициент шероховатости n = 0,0225, уклон дна канала i = 0,0005.
Задача 11.25
Определить, какой уклон необходимо придать круглой трубе (рис. 11.2) для пропуска расхода Q = 53 м3/с при следующих данных: радиус r = 1,9 м, глубина наполнения h = 209 см, коэффициент шероховатости n = 0,025.
Купить задачу 11.25
Задача 11.29
Определить глубину воды в лотке параболического поперечного сечения (рис. 11.3) при следующих данных: параметр p = 0,35 м; расход Q = 4 м3/с; коэффициент шероховатости n = 0,012; уклон дна i = 0,0015.
Купить задачу 11.29
Задача 11.31
Для русла круглого поперечного сечения радиусом r (рис. 11.2) определить относительную глубину заполнения h/r, при которой расход в русле будет максимальным.
Купить задачу 11.31
Задача 11.32
Для русла трапецеидального поперечного гидравлически наивыгоднейшего сечения (рис. 11.1) с шириной по дну b = 2,5 м определить ширину русла по свободной поверхности. Коэффициент заложения откосов m = 1,0.
Купить задачу 11.32
Задача 11.34
Для русла круглого поперечного сечения радиусом r (рис. 11.2) определить смоченный периметр, при котором расход в русле будет максимальным.
Купить задачу 11.34
Задача 11.36
Для русла круглого поперечного сечения радиусом r (рис. 11.2) определить площадь поперечного сечения потока, при котором расход в русле будет максимальным.
Купить задачу 11.36
Задача 11.37
Определить размеры гидравлически наивыгоднейшего прямоугольного сечения лотка, если расход в лотке Q = 2 м3/с, а скорость течения воды υ = 1 м/с.
Купить задачу 11.37
Задача 11.41
Сравнить пропускную способность облицованных бетоном (n = 0,017) каналов с одинаковой площадью живого сечения потока, если форма сечения каналов: равносторонний треугольник и полукруг.
Купить задачу 11.41
Задача 11.42
Сравнить пропускную способность облицованных бетоном (n = 0,017) с одинаковой площадью гидравлически наивыгоднейших сечений каналов: прямоугольник и трапеция с коэффициентом заложения откосов m = 1.
Задача 11.43
Установить размеры и необходимый уклон канала с гидравлически наивыгоднейшей формой поперечного сечения канала, если расход воды Q = 14,0 м3/с, средняя скорость движения υ = 3,5 м/с, а коэффициент заложения откосов m = 2,0. Канал облицован булыжником (n = 0,035).
Купить задачу 11.43
Задача 11.44
Водоподводящий канал длиной l = 2000 м, связывающий между собой два водоема, имеющих разность уровней ΔH = 1,5 м, должен пропускать расход Q = 24,0 м3/с. Определить глубину заполнения канала при гидравлически наивыгоднейшем сечении, если канал прокладывается непосредственно в плотном грунте (n = 0,025) с коэффициентом заложения откосов m = 1,75.
Купить задачу 11.44
Задача 11.45
Каков уклон должен быть придан деревянному лотку (n = 0,013) прямоугольного сечения шириной b = 0,6 м, чтобы при глубине заполнения h = 0,3 м пропускная способность его равнялась пропускной способности полукруглого железного канала с таким же живым сечением и уклоном дна i = 0,005.
Купить задачу 11.45
Задача 11.47
Определить расход воды в канале, облицованном бетоном (n = 0,017), если радиус r = 1 м; глубина заполнения канала h = 2 м, уклон дна i = 0,00007 (рис. 11.8).
Купить задачу 11.47
Задача 11.49
Определить расход воды в реке шириной b = 320 м, средней глубиной h = 1,2 м с уклоном свободной поверхности воды i = 0,0001. Коэффициент шероховатости n = 0,025. Гидравлический радиус принять равным h.
Задача 11.53
Установить глубину протекания потока и определить, будет ли размываться трапецеидальное русло, если площадь живого сечения потока ω = 2,5 м2, ширина русла по дну b = 1 м, коэффициент заложения откосов т = 1,5, расход воды Q = 3,5 м3/с, грунт — плотная глина.
Купить задачу 11.53
Задача 12.10
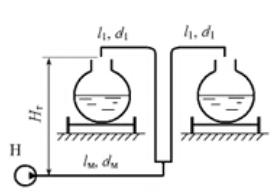
Насос Н закачивает Бензин в две железнодорожные цистерны вместимостью V = 50 м3 каждая по трубам, длины и диаметры которых l1 = 18 м, lм = 100 м, d1 = 100 мм, dм = 156 мм. Определить давление, с которым должен работать насос, если бензин плотностью ρ = 750 кг/м3 и с кинематическим коэффициентом вязкости ν = 0,01 Ст закачивается в течение часа, геодезическая высота подъема бензина Нг = 5 м. Трубы гидравлические гладкие.
Задача 12.32
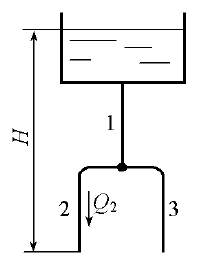
Определить напор Н, при котором расход в трубе 2 Q2 = 2 л/с, приведенные длины l1 = 60 м, l2 = 25 м, l3 = 30 м, диаметры d1 = d3 = 60 мм, d2 = 50 мм (рис. 12.36). Шероховатость труб Δ = 0,02 мм, а давление в конечных сечениях труб 2 и 3 атмосферное.
Купить задачу 12.32
Задача 12.34
Две параллельные одинаковые трубы длиной l каждая и диаметром d заменяются одной трубой той же длины, площадь сечения которой равна суммарной площади сечения двух заменяемых труб. Определить, как изменится пропускная способность трубы при неизменном напоре при ламинарном режиме и при турбулентном в области гидравлически гладких труб (формула Блазиуса).
Купить задачу 12.34
Задача 13.1
Показание вакуумметра, установленного на всасывающем патрубке диаметром d1 = 60 мм, рвак = 0,4 · 105 Па, а показание манометра, установленного на нагнетательном патрубке диаметром d2 = 50 мм, рм = 5,8 · 105 Па, причем ось нагнетательного патрубка располагается на z = 0,6 м ниже центра манометра и на z = 0,4 м выше оси всасывающего патрубка. Определить КПД центробежного насоса, если бак вместимостью 2,4 м3 заполняется при работе насоса за 9 мин, а мощность потребляемая электродвигателем N2 = 5,0 кВт при КПД электродвигателя ηэд = 0,93.
Задача 13.34
При испытании насоса получены следующие данные: избыточное давление на выходе из насоса рн = 0,35 МПа, вакуум перед насосом hв = 294 мм рт.ст., подача Q = 6,5 л/с, крутящий момент на валу насоса М = 41 Н · м; частота вращения вала насоса n = 800 об/мин. Определить полезную мощность насоса, потребляемую мощность и КПД насоса. Диаметры всасывающего и напорного трубопроводов считать одинаковыми.
Купить задачу 13.34
Задач, которых нет на странице, Вы можете заказать