Заказать задачу
Сборник задач по гидравлике: Учеб. пособие для вузов /Под ред. В. А. Большакова.- 4-е изд., перераб. и доп.-Киев: Вища школа. Головное изд-во, 1979. 336 с.
Глава I.1. Гидростатическое давление
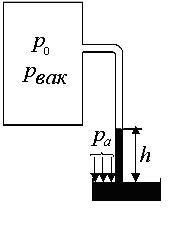
I.1. Найти давление на свободной поверхности в закрытом сосуде с бензином, если уровень жидкости в открытом пьезометре (рис. I.1) выше уровня жидкости в сосуде на h = 2 м, а атмосферное давление pа = 100 кПа.
Купить задачу I.1
I.2. В U-образный сосуд налиты ртуть и вода (рис. I.2). Линия раздела жидкостей расположена ниже свободной поверхности ртути на hрт = 8 см. Определить разность уровней h в обеих частях сосуда.
Купить задачу I.2
I.3. Определить глубину воды в море (ρ = 1020 кг/м3 ), на которой избыточное давление равно: а) 50 кПа; б) 75 кПа.
Купить задачу I.3а
Купить задачу I.3б
I.4. Определить, насколько увеличится давление, которое испытывает водолаз в морской воде (ρ = 1020 кг/м3 ) при переходе: а) от глубины h1 = 15 м к глубине h2 = 30 м; б) от глубины h1 = 10 м к глубине h2 = 20 м.
Купить задачу I.4а
Купить задачу I.4б
I.5. Определить полное и избыточное давление воды на дно открытого сосуда, если атмосферное давление pа = 100 кПа, а глубина воды в сосуде равна: а) h = 2,5 м; б) h = 4 м.
Купить задачу I.5а
Купить задачу I.5б
I.6. К резервуару, заполненному газом давлением p0, присоединена трубка, опущенная в сосуд с ртутью (рис. I.3). Требуется: а) определить давление p0 в резервуаре, если ртуть поднялась в трубке на высоту h= 23 см; б) найти высоту h, на которую поднимается ртуть в трубке, если вакуум в резервуаре составляет 3 м вод.ст., а атмосферное давление pа = 98,1 кПа.
Купить задачу I.6а
Купить задачу I.6б
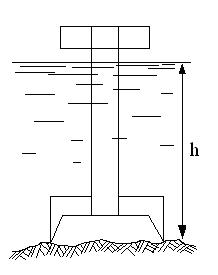
I.7. Давление воздуха в рабочей камере кессона (рис. I.4.) зависит от глубины его погружения h. Определить : а) манометрическое давление воздуха в камере кессона при глубине h = 30 м; б) допустимую глубину погружения h кессона при условии, что манометрическое давление в его камере не превышает 250 кПа. Атмосферное давление pа = 100 кПа, плотность воды ρ = 1000 кг/м3 .
Купить задачу I.7а
Купить задачу I.7б
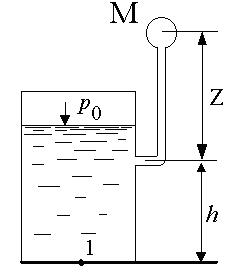
I.8. Пружинный манометр подключен к сосуду с водой на высоте h= 1 м от дна. Центр манометра находится выше точки подключения его к сосуду на z = 1 м ( рис. I.5). Определить: а) избыточное давление на дно при показании манометра pм = 160 кПа; б) показание манометра при абсолютном давлении на поверхности воды в сосуде p0 = 180 кПа и атмосферном давлении pа = 180 кПа и Н = 1,5 м.
I.9. Открытые сообщающиеся сосуды (рис. I.6) заполнены различными жидкостями (ρ1 = 750 кг/м3; ρ2 = 1250 кг/м3). Найти: а) расстояние от линии раздела АВ до уровня жидкости в каждом сосуде h1 и h2, если разность уровней жидкостей в сосудах h= 10 см; б) разность уровней h при h1 = 40 см.
I.10. Определить вакуум в резервуаре (рис. I.7), если: а) h1 =100 мм; h2 = 200 мм; атмосферное давление pа = 100 кПа; б) h1 = 150 мм; h2 = 250 мм; pа = 98,1 кПа.
Купить задачу I.10а
I.11. Определить плотность жидкости в открытых сообщающихся сосудах (рис. 1.6), если: а) ρ2 = 13600 кг/м3; h1 = 43,4 см; h2 = 39,4 см; б) ρ2 = 1250 кг/м3; h1 = 80 см; h2 = 32 см.
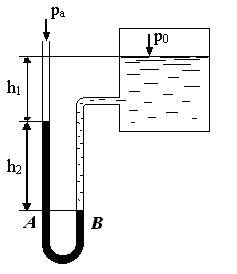
I.12. U-образный ртутный манометр подключён к закрытому резервуару, заполненному водой (рис. 1.8). Определить: а) давление на поверхности воды в резервуаре, если h1 = 150 мм; h2 = 250 мм; pа = 98,1 кПа. Определить: б) высоту ртутного столба h2, если p0 = pа, а h1 = 252 мм.
I.13. Каково показание h2 U-образного ртутного манометра (рис. 1.8), подключённого к резервуару с водой, если: а) давление на поверхности воды в резервуаре, если h1 + h2 = 400 мм; p0 = 110 кПа; pа = 100 кПа; б) давление на поверхности воды в резервуаре, если h1 + h2 = 500 мм; p0 = 125 кПа; pа = 9,81 кПа.
I.14. Определить разность давлений в резервуарах А и В, заполненных бензином, если показание дифференциального ртутного манометра hр равно (рис. 1.9): а) 70 мм; б) 100 мм.
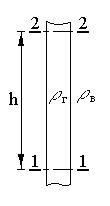
I.15. Определить манометрическое давление в сечении 2 – 2 газового столба (рис. I.10) и построить эпюру давления, если в сечении 1 – 1 рм1 = 981 Па (100 мм вод. ст.), расстояние между сечениями h = 15 м, плотность наружного воздуха ρв = 1,2 кг/м3, плотность газа в стояке: а) ρг = 0,7 кг/м3; б) ρг = 1,4 кг/м3; в) ρг = 1,2 кг/м3.
I.16. Определить, на каких этажах (верхних или нижних) подача газа к газовым приборам будет больше, если плотность наружного воздуха 1,2 кг/м3, а плотность газа в стояке: а) 0,8 кг/м3; б) 1,2 кг/м3; в) 1,4 кг/м3.
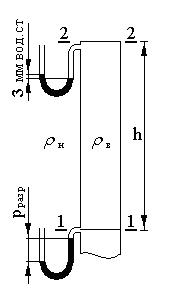
I.17. Определить разрежение в нижнем сечении 1 — 1 вытяжной трубы высотой h = 4 м (рис. I.11), если наружное давление в верхнем сечении 2 — 2 на 3 мм вод. ст. меньше внутреннего из-за действия ветра; плотность наружного воздуха ρн = 1,2 кг/м3; плотность воздуха ρв в трубе: а) 0,9 кг/м3; б) 0,75 кг/м3.
Построить эпюру разрежения и давления.
Заказать задачу
Глава I.2. Сила гидростатического давления на плоскую поверхность
I.18. Определить величину и точку приложения силы гидростатического давления воды на вертикальный щит шириной b = 2 м, если глубина воды перед щитом H = 2,7 м (рис. I.13).
I.19. На какой глубине должна находиться опора щита О (рис. I.15), чтобы при h1 > 4,2 м он открывался автоматически, если: а) h2 = 1,8 м; угол β = 30°; б) h2 = 2,5 м; угол β = 45°.
Указание. Весом щита пренебречь.
I.20. Вертикальный щит, перегораживающий прямоугольный канал шириной b = 0,8 м, изготовлен из пяти досок шириной a = 30 см. Определить толщину доски, считая допускаемое напряжение для дерева [σ] = 7 МПа. Глубина воды в канале h = 1,45 м (рис. I.16).
I.21. Определить силу давления воды на дно сосуда и каждую из четырёх опор (рис. I.17). Собственным весом сосуда пренебречь.
I.22. Проверить устойчивость плотин (рис. I.18) на опрокидывание при трёх различных соотношениях между плотностью кладки и плотностью воды: ρк/ρв < 2; ρк/ρв = 2; ρк/ρв > 2.
I.23. Отверстие в боковой вертикальной стенке закрытого резервуара, представляющее собой равносторонний треугольник со стороной b = 0,5 м, закрыто крышкой (рис. I.19). Определить силу давления воды на крышку, если горизонтальное основание треугольного отверстия расположено на глубине H = 1,5 м, а манометрическое давление на свободной поверхности pм равно: а) 0; б) 50 кПа.
I.24. Два сосуда А и В (рис. I.20) одинакового диаметра заполнены водой. Сосуд А открыт. В верхнюю крышку сосуда В вставлена тонкая трубка. Определить силу давления воды на дно каждого сосуда, если: а) На = 2 м; Нв = 10 м; h = 1 м; б) На = 3 м; Нв = 3 м; h= 1 м.
I.25. Гидравлический домкрат (рис. I.21) имеет диаметр большего поршня D = 250 мм, а диаметр меньшего поршня d = 25 мм; коэффициент полезного действия η = 0,8. Плечи рычага: a= 1 м и b = 0,2 м. Определить: а) усилие Р, которое необходимо приложить на конце рычага, чтобы поднять груз G = 20 кН; б) максимальную грузоподъемность домкрата G из условия, что усилие Р на конце рычага не будет превышать 100 Н.
I.26. Тонкостенный резервуар с размерами В xВ xН = 3 x 3 x 2 м опущен в воду вверх дном (рис. I.22). Определить: а) вес резервуара G, а также глубину его погружения h, если показание ртутного U-образного манометра hрт = 50 мм, а атмосферное давление pа = 98,1 кПа; б) показание ртутного U-образного манометра hрт и глубину погружения резервуара h, если его вес G = 44 100 Н.
У к а з а н и е. Подъемной силой пренебречь и считать, что сила тяжести резервуара приложена ко дну.
I.27. Длина подпорной стенки (рис. I.23) l =5 м. Глубина воды перед стенкой h = 1,8 м, коэффициент трения кладки о грунт fтр = 0,4. Проверить устройство стенки на опрокидывание и на скольжение, если плотность кладки: а) ρк = 2500 кг/м3; б) ρк = 1800 кг/м3.
I.28. Найти величину и точку приложения равнодействующей сил гидростатического давления воды на прямоугольный вертикальный щит шириной b = 2,8 м, если глубина воды: а) с одной стороны щита h1 = 3 м, а с другой — h2 = 2 м; б)h1 = 2,7 м; h2 = 1,5 м.
I.29. Для регулирования уровня воды в напорном баке установлен поворачивающий щиток, который должен открывать квадратное отверстие а x а = 0,4 x 0,4 м в вертикальной стенке при заданном уровне Н (рис. I.24). Найти глубину hпогружения шарнира О и силу давления воды на щиток при: а) Н = 2 м; б) Н = 1,5 м.
I.30. Прямоугольный вертикальный щит, перегораживающий прямоугольный канал шириной b = 4м, находится в пазах (рис. I.25). Вес щита G= 4,9 кН, коэффициент трения щита в пазах fтр = 0,5. Определить усилие Т, необходимое для поднятия щита, если глубина воды: а) с одной стороны щитаh1 = 3 м, с другой — h2 = 1 м; б) h1 = 3 м;h2 = 2 м.
I.31. Круглое отверстие d = 40 см в вертикальной стенке резервуара с водой перекрыто плоским клапаном. Найти величину и точку приложения силы, прижимающей клапан к стенке, если центр отверстия находится ниже свободной поверхности жидкости: а) на 0,5 м; б) 3 м.
I.32. Для плоских прямоугольных фигур (рис. I.26) построить эпюры избыточного гидростатического давления.
У к а з а н и е. Эпюры строить для участков, показанных сплошной линией.
I.33. Определить натяжение троса, удерживающего прямоугольный щит шириной b = 2м при глубине воды перед щитом h = 1,8м (рис. I.27), если угол наклона щита к горизонту: а) α = 60˚; б) α = 45˚.
У к а з а н и е. Весом щита пренебречь.
I.34. Прямоугольный щит длиной а = 5 м и шириной b = 5 м закреплен шарнирно в точке О (рис. I.28); Н1 = 4 м; Н2 = 2 м; α = 60˚. Определить: а) реакцию опор А и О; б) усилие Т, необходимое для подъема щита.
I.35. Определить горизонтальную и вертикальную составляющие силы давления воды на 1м ширины плотины (рис. I.29), если: а) h = 3 м; l1 =1 м; l2 = 2,2 м; б) h=2 м; l1 =0; l2 =2,2 м.
I.36. В вертикальной стенке закрытого резервуара с нефтью (рис. I.30) имеется квадратное отверстие b x b= 0,5 x 0,5 м. Определить: а) величину и точку приложения силы давления жидкости на крышку, перекрывающую это отверстие, если напор Н = 1 м, показание ртутного U-образного манометра, подключенного к резервуару, h = 300 мм и атмосферное давление pа = 98,1 кПа; б) при каком давлении на свободной поверхности p0 крышка будет находиться в равновесии.
I.37. Прямоугольный поворотный затвор размерами bx a = 1 x 2м перекрывает выход из резервуара (рис. I.31). На каком расстоянии х необходимо расположить ось затвора О, чтобы при открывании его в начальный момент необходимо было преодолевать только трение в шарнирах, если глубина в резервуаре: а) Н = 3 м; б) Н = 4 м?
Заказать задачу
Глава I.3. Сила гидростатического давления на криволинейную поверхность
I.38. Определить силу гидростатического давления воды на 1м ширины нижней криволинейной части сооружения (рис. I.33), если Н = 1,5 м, r = 0,5 м.
I.39. Определить величину и направление силы гидростатического давления воды на 1м ширины вальцового затвора диаметром D= 1,5 м (рис. I.34).
I.40. Определить силу гидростатического давления воды на 1м ширины вальцового затвора диаметром d = 1,2 м (рис. I.35) при h1 = 1,2 м, если: а) h2 = 0,5 м; б) h2 = 0,7 м.
I.41. Определить силу давления воды на 1м ширины затвора, перекрывающего канал между двумя смежными камерами (рис. I.36),если глубина воды в левой камере h1 = 5 м; в правой h2 = 2,5 м; R = 4; а = 2 м; α = 15˚; β = 30˚.
I.42. Цилиндр радиусом r = 25 см и длиной l =100 см перекрывает отверстие в дне резервуара размерами ax b = 30 x 100 см (рис. I.37). Определить: а) силу давления воды на цилиндр при Н = 3м; p0 = pа; б) при какой глубине Н цилиндр всплывает, если его вес G = 600Н, а давление на свободной поверхности p0 = 80 кПа.
I.43. Построить тела давления для криволинейных поверхностей, приведенных на рис. I.38.
I.44. Круглое отверстие радиуса R = 20 см в дне резервуара с водой перекрывается клапаном-полусферой такого же радиуса (рис. I.39), вес которого G = 200Н. Вычислить: а) силу Т, необходимую для поднятия клапана при напоре Н = 2,5 м, если давление на свободной поверхности ; p0 = pа = 100 кПа; б) при каком напоре Н клапан откроется автоматически, если p0 = 80 кПа, а pа = 100 кПа.
I.45. Круглое отверстие в вертикальной стенке закрытого резервуара с водой перекрыто сферической крышкой (рис. I.40). Радиус сферы R = 0,5 м; угол α = 120˚; глубина погружения центра тяжести отверстия Н = 1 м. Определить силу давления жидкости на крышку при манометрическом давлении на ее свободной поверхности: а) 147 кПа; б) 98,1 кПа.
I.46. Стальная трубка с внутренним диаметром D=600 мм работант под давлением p= 3 МПа. Найти: а) необходимую толщину стенок трубы, если допустимое напряжение для стали [σ] = 150 МПа; б) максимально допустимое давление при толщине стенки трубы δ = 4 мм.
I.47. Определить величину и направление силы давления воды на 1 м ширины затвора, представляющего собой четверть кругового цилиндра (рис. I.41) радиуса R, равного: а) 1,5 м; б) 2 м.
I.48. Определить величину и направление силы давления воды на 1 м ширины затвора (рис. I.42), если: а) R= 1 м; Н = 2 м; б) R= 2 м; Н = 2,5м.
I.49. Определить величину и направление силы давления воды на 1 м ширины щита, показанного на рисунке I.43, если: а) R= 5 м; α= 45˚; β = 35˚; б) R= 2,5 м; α= 45˚; β = 35˚.
I.50. Найти величину и направление силы давления воды на 1 м ширины секторного затвора радиуса R = 2,5 м (рис. I.44), если: а) β = 45º б) β = 60º в) β = 75º.
I.51. Изогнутая труба диаметром 500 мм (рис. I.45) находится под давлением 1 МПа. Определить силу давления воды на колено, а также открывающее и сдвигающее усилия, которые возникают на стыках колена с прямолинейными участками трубы, если угол поворота трубы α равен: а) 60˚; б) 90˚; в) 120˚.
I.52. Определить величину и направление силы давления воды на цилиндрический затвор (рис. I.46) диаметром D=2 м и длиной L = 5 м, перегораживающий прямоугольный канал шириной b = 5 м, если глубина воды: а) с одной стороны щита Н1 = 3 м; с другой – h2 = 1 м; б) Н1 = 2,5 м; h2 = 1 м.
Глава I.4. Плавание тел
I.53. Автомобиль весом Ga= 30 кН установлен на паром размерами L = 8 м, В = 4 м, Н = 1 м (рис. I.48). Проверить устойчивость парома, если его вес Gп = 50 кН приложен на половине его высоты, а центр тяжести автомобиля находится на высоте hа = 1 м от верхней плоскости парома. Установить, как изменится метацентрическая высота hм, если на автомобиль будет уложен груз G= 30 кН, центр тяжести которого расположен на высоте hг = 2 м от верхней плоскости парома.
I.54. Цилиндр диаметром D = 50 см и высотой Н = 20 см, изготовленный из дерева (ρ = 800 кг/м3 ), плавает по воде таким образом, что его ось направлена вертикально. Требуется: а) проверить остойчивость цилиндра; б) найти высоту цилиндра Н, при которой он начинает терять остойчивость.
I.55. Плавучий железобетонный тоннель с наружным диаметром D = 10 м и толщиной стенок δ = 0,4 м удерживается от всплытия тросами, расположенными попарно через каждые 25 м длины тоннеля (рис. I.49). Определить: а) натяжение тросов, если вес 1 м дополнительной нагрузки по длине q = 9,81 кН, плотность бетона ρб = 2450 кг/м3 и угол α= 60˚; б) как изменится натяжение тросов при уменьшении наружного диаметра тоннеля на 1 м.
I.56. Длина прямоугольного понтона l = 5 м, ширина b = 2,5 м и высота Н = 1 м. Вес понтона 8,5 кН. Проверить понтон на остойчивость: а) без нагрузки; б) при максимальной нагрузке G, при которой высота бортов над ватерлинией 0,2 м. Центры тяжести понтона и дополнительной нагрузки расположены на расстоянии 0,5 м от дна.
I.57. Для перевозки автомобилей весом до 30 кН через реку сооружается плот из бревен диаметром d = 0,25 м и длиной l = 9 м. Определить: а) сколько бревен нужно для сооружения плота, способного удержать груз G = 35 кН, если плотность дерева ρд = 800 кг/м3; б) будет ли плот остойчив, если все бревна уложить вплотную, поровну в каждом из двух рядов, а центр тяжести автомобиля расположен на высоте h= 1 м над верхней плоскостью плота.
I.58. Бетонная плита весит в воздухе 1250 Н, а в воде 750Н. Определить: а) плотность бетона; б) вес этой плиты в бензине (ρб = 750 кг/м3 ).
I.59. По окончании погрузки 1250 м3 песка осадка баржи увеличилась на 1 м. Определить: а) плотность песка, если площадь плоскости плавания баржи Ω = 2000 м3; б) величину изменения осадки баржи, если вместо песка на баржу будет погружено 2000 м3 извести плотностью 800 кг/м3.
I.60. Прямоугольная деревянная шаланда весом 0,8 МН и длиной 30 м должна иметь полезное водоизмещение 3 МН. Определить: а) необходимую ширину шаланды В и высоту ее бортов Н при условии, что метацентрическая высота hм = 1 м, высота бортов нагруженной шаланды над ватерлинией h= 0,5 м, а центр тяжести ее совпадает с центром тяжести поперечного сечения; б) как необходимо изменить ширину шаланды В и высоту ее бортов Н, чтобы ее полное водоизмещение стало равным 5 МН.
I.61. Прямоугольный деревянный брус длиной l = 5 м, шириной b = 35 см и высотой h = 25 см плотностью ρд = 750 кг/м3 плавает по воде. Определить: а) остойчивость бруса в двух положениях, показанных на рис. I.50. б) при каком отношении b/h брус еще будет остойчивым ( граничное положение).