У.4
Часть задач есть решенные, контакты
Приклад 1. Барометр, що встановлений на рівні моря, показує hрт = 760 мм рт.ст. Температуру повітря вважати сталою t = 15°C. Визначити тиск повітря на висоті h = 2 км від рівня моря.
Приклад 2. До закритого резервуара приєднано ртутний манометр,показання якого становить h = 0,4 м (рис. 1.3). Атмосферному тиску відповідає 738 мм рт.ст. Визначити абсолютний тиск повітря у резервуарі, якщо H = 1м.
Приклад 3. Визначити вакуумметричний тиск повітря у резервуарі (рис. 1.4), якщо задані: а) h1 = 150 мм, h2 = 230 мм,атмосферний тиск pа = 100 кПа; б) h1 = 250 мм, h2 = 300 мм, pа = 100 кПа.
1.1. Визначити:
а) на якій висоті над рівнем моря тиск повітря становить 50,5 кПа;
б) яким буде тиск повітря на висоті 730 м?
Температуру повітря прийняти 15°C та вважати сталою, густина повітря за t = 15°C пов 3 м ρ = 1,22 кг. Тиск рідини на рівні моря відповідає 760 мм рт.ст.
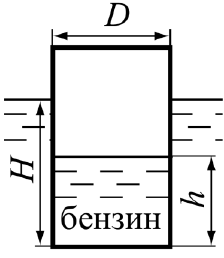
Задача 1.2. До закритого резервуара, що заповнений рідиною (рис. 1.5), приєднаний п’єзометр. Визначити манометричний тиск на вільній поверхні у резервуарі pм, а також манометричний тиск у точці A, якщо: а) показання п’єзометра h = 0,4 м, глибина h1 = 0,9 м, рідина – нафта, 3 мρ = 850 кг; б) h = 0,7 м, 1 м h1 =, рідина – вода; в) h = 0,5 м, h1 =1 м, рідина – бензин, м3ρ = 760 кг.
Вартість: 40 грн (Варіант б)
Задача 1.3. Визначити: а) на яку висоту підніметься вода у трубці (рис. 1.6), якщо абсолютний тиск повітря всередині балона pпов 0_7_=_8 = 80 кПа; б) абсолютний тиск повітря всередині балона, якщо вода піднімається у трубці на висоту h = 0,7 м.
Задача 1.4. Визначити висоту ртутного стовпчика h2 (рис. 1.7), якщо: а) манометричний тиск нафти (н 3 мρ = 800 кг) у точці A становить 11 pA = 50 кПа, а висота стовпчика нафти дорівнює h1 = 60 см; б) pA = 80 кПа, h1 = 50 см; в) pA = 40 кПа, h1 = 70 см.
Вартість: 40 грн (Варіант а)
Задача 1.5. Пружинний манометр (рис. 1.8) підключений до резервуара з водою на висоті h = 1 м від дна. Центр манометра розташований вище точки підключення його до посудини на z = 1 м.
Визначити: а) надлишковий тиск на дно, якщо показання манометра pм = 160 кПа; б) показання манометра при абсолютному тиску на поверхні води у резервуарі p0 = 180 кПа, атмосферному тиску pа =100 кПа та H = 1,5 м.
Вартість: 40 грн (Варіант а, б)
Задача 1.6. Побудувати сумарні епюри тиску рідини на стінки АВС та ABCDEF для таких випадків (рис. 1.9): а) h1 = 1,5 м, h2 = 0,7 м, h3 = 1,0 м, pвак = 4 кПа, 3 мρ = 1000 кг; б) h1 = 2,0 м, h2 = 0,8 м, h3 =1,6 м, pвак = 5 кПа, 3 мρ = 750 кг.
Вартість: 50 грн (Варіант б)
Задача 1.7. У резервуарі, що поділений перегородкою на дві частини, перебуває вода із температурою t1 і t2 (рис. 1.10). У нижній частині перегородки є невеликий отвір.
Визначити різницю рівнів Dh, при якій не буде відбуватися перетікання рідини між секціями, якщо h = 2 м, h1 =1 м і температури відповідно: а) t°C1 =10 і t С°2 = 40; б) t C°1 = 0 і t С°2 = 60; в) t°C1 = 6 і t С°2 = 50.
Задача 1.8. У закритому резервуарі (рис. 1.11) вода у п’єзометрі піднялася на висоту h1 =1,5 м.
Визначити: а) значення тиску p0, що прикладений до поверхні води, якщо точка підключення п’єзометра розташована на глибині h = 0,8 м; б) глибину h, якщо тиск на вільній поверхні води у резервуарі p0 = 7,0 кПа.
Задача 1.9. До закритого резервуара приєднаний ртутний манометр,показання якого становить h (рис. 1.3). Атмосферному тиску відповідає 738 мм рт.ст. Визначити висоту H, якщо абсолютний тиск повітря у резервуарі: а) p = 40 кПа, h = 0,4 м; б) p = 30 кПа, h = 0,5 м.
Задача 1.10. Закритий резервуар, що заповнений маслом (рис. 1.12), перебуває під тиском. Відносна питома вага масла 0,75. Для вимірювання рівня масла у резервуарі з правого боку виведений п’єзометр, показання якого h = 0,8 м. Лівий п’єзометр призначений для вимірювання тиску у резервуарі.
Визначити: а) висоту лівого п’єзометра z для вимірювання максимального манометричного тиску у резервуарі pм = 6 кПа; б) абсолютний тиск у резервуарі, якщо показання лівого п’єзометра z = 1,5 м, а резервуар знаходиться на висоті 1500 м над рівнем моря.
Вказівка. Відносна питома вага – це відношення питомої ваги даної рідини до питомої ваги води при 4°C. У даному випадку0,75 γγмас = .
Вартість: 40 грн (Варіант а, б)
Задача 1.11. У газовому стояку показання п’єзометра на першому поверсі дорівнює h1 = 100 мм вод.ст., густина газу у стояку г 3 мρ = 0,7 кг (рис. 1.13). Густина зовнішнього повітря п 3 мρ = 1,29 кг. Визначити показання п’єзометра h2, якщо висота: а) H = 60 м; б) H = 40 м.
Задача 1.12. Резервуар знаходиться на 2 км вище рівня моря. Визначити: а) манометричний тиск води у резервуарі (рис. 1.14), якщо ртутний манометр розташований таким чином, що нижній рівень ртуті, який знаходиться над центром резервуара на висоті H = 5 м, показує h = 700 мм; б) висоту розташування нижнього рівня ртуті H над центром резервуара, якщо манометричний тиск води у резервуарі дорівнює p = 160 кПа, а h = 720 мм.
Вартість: 40 грн (Варіант б)
Задача 1.13. У резервуар діаметром D = 4 м (рис. 1.15) налито воду, на вільній поверхні якої абсолютний тиск p0. На глибині H приєднаний манометр М, що показує тиск p = 40 кПа.
Визначити: а) глибину H та об’єм води у резервуарі, якщо тиск p0 = 130 кПа; б) абсолютний тиск на поверхні води p0, якщо об’єм води у резервуарі W = 14 м3.
Задача 1.14. Побудувати сумарні епюри тиску рідини на стінки ABC та MON (рис. 1.16) для таких випадків: а) h1 = 0,5 м, h2 =1,0 м, pм =100 кПа, 3 м ρ = 850 кг; б) 0,4 м h1 = , h2 =1,2 м, pм = 30 кПа, 3 м ρ = 1000 кг.
Задача 1.15. Визначити надлишковий тиск рідини в трубі за показаннями ртутного манометра (рис. 1.17).Відмітки рівнів ртуті від осі труби: z1 =1,75 м, z2 = 3 м, z3 = 1,5 м, z4 = 2,5 м. Розрахунки провести: а) для води (3 мρ = 1000 кг); б) длябензину (б 3 мρ = 700 кг).
Задача 1.16. До закритого резервуара приєднаний вакуумметр (рис. 1.18). Густина ртуті рт 3 мρ = 13600 кг, повітря пов 3 мρ = 1,29 кг, глибина h =1,5 м, атмосферному тиску відповідає hа = 760 мм рт.ст.
Визначити: а) показання ртутного манометра, якщо абсолютний тиск повітря у резервуарі pабс = 65 кПа; б) абсолютний тиск повітря у резервуарі pабс, якщо показання ртутного вакуумметра hрт = 0,2 м. Яким при цьому буде показання пружинного вакуумметра?
Задача 1.17. Визначити надлишковий (або вакуумметричний) та абсолютний тиск у точках 1, 2, 3, 4, 5, 6 резервуара, що заповнений рідиною (рис. 1.19), та у герметично закритих вертикальних трубках I і II, що занурені у неї, якщо задані: а) h1 = 3,5 м, h2 = 2,5 м, h3 = 1,0 м, h4 = 4,0 м, рідина – вода; б) h1 = 2,0 м, h2 =1,0 м, h3 = 1,0 м, h4 = 5,0 м, рідина – нафта (3 мρ = 850 кг).
Вартість: 50 грн (Варіант а)
Задача 1.18. Закритий резервуар заповнений водою (рис. 1.20). Висота рівня масла у U-подібному манометрі дорівнює H = 1 м. Перевищення рівня масла над кришкою резервуара h = 330 мм, густина маслам 3ρ = 880 кг.
Визначити: а) показання манометра, що приєднаний на відстані b =120 мм до резервуара; б) висоту H, якщо показання манометра pм = 2 кПа, b =120 мм.
Вартість: 40 грн (Варіант а)
Задача 1.19. Визначити, на яких поверхах (верхніх чи нижніх) подача газу до газових пристроїв буде більшою і побудувати епюри тиску, якщо густина зовнішнього повітря 3 м 1,2 кг, а густина газу у стояку: а) 3 м 0,8 кг; б) м 31,2 кг; в) м 31,4 кг.
Вказівка. Подача газу до газових пристроїв буде більшою на тих поверхах, де манометричний тиск газу у стояку буде вище.
Задача 1.20. Знайти вакуумметричний тиск повітря у резервуарі (рис. 1.21), що знаходиться на1700 м над рівнем моря, якщо задані: а) h1 = 100 мм, h2 = 120 мм, h3 = 170 мм, густина ртуті рт 3 мρ = 13600 кг, атмосферний тиск pа = 100 кПа; б) h1 = 150 мм, 2 180 мм h = , h3 = 230 мм, pа = 100 кПа.
Вартість: 50 грн (Варіант б)
Задача 1.21. Закритий резервуар заповнений рідиною із густиною 3ρ = 880 кг. На відстані 0,2 м від дна резервуара приєднаний манометр M, до верхньої частини – вакуумметр V, який показує тиск pвак = 12 кПа (рис. 1.22). Побудувати епюру тиску на вертикальну стінку резервуара та визначити: а) показання манометра, якщо глибина води у резервуарі H = 6 м; б) глибину H у резервуарі, якщо манометр показує pм = 50 кПа.
Задача 1.22. Закритий резервуар заповнений рідиною із густиною 3ρ = 880 кг. Для вимірювання тиску у резервуарі використовують ртутний вакуумметр (рис. 1.23). У відкритому кінці манометричної трубки над ртуттю розташований шар води висотою h1 = 15 см. Задані також висоти h2 = 25 смта h3 = 35 см.
Визначити: а) абсолютний тиск на поверхні рідини у резервуарі, якщо атмосферному тиску відповідає 750 мм рт.ст; б) показання барометра при відомому абсолютному тиску на поверхні рідини у резервуарі pабс = 70 кПа.
Вартість: 40 грн (Варіант б)
Задача 1.23. Закритий та відкритий резервуари (рис. 1.24), що заповнені рідиною із густиною1 3 мρ = 900 кг, з’єднані між собою трубкою, в якій міститься вода (2 3 мρ = 1000 кг), h1 = 50 см, h2 = 55 см. Визначити: а) манометричний тиск pм на поверхні рідини у закритому резервуарі, якщо h =10 см; б) висоту h, якщо манометричний тиск на поверхні рідини у закритому резервуарі pм = 0,6 кПа.
Задача 1.24. Визначити: а) на якій позначці z зупиниться рівень ртуті у п’єзометрі, якщо при манометричному тиску у трубі A= 39,24 кПа А p та показнику h = 24 см система перебуває у рівновазі (рис. 1.25); б) манометричний тиск у трубі, якщо z = 80 см, а показання h = 20 см.
Задача 1.25. У резервуарі і трубі, що показані на рисунку (рис. 1.26), вода перебуває в стані рівноваги. Глибина води у верхньому резервуарі h =1 м. Визначити: а) показання ртутного вакуумметра hрт, якщо висота H = 2,5 м; б) висоту H при hрт = 300 мм рт.ст.
Задача 1.26. Побудувати епюри тиску рідини на стінки та визначити сумарну епюру для таких випадків: а) ABCDEF та MNO (рис. 1.27) h =1,2 м, h1 = 1,0 м, h2 = 0,5 м, 3 мρ = 1000 кг; 19б) ABCD та MN (рис. 1.28) h = 2,0 м, h1 = 0,4 м, h2 =1,2 м, p = 95 кПа, 3 мρ = 800 кг.
Вартість: 50 грн (Варіант а)
Задача 1.27. Диференціальний манометр, що складається із двох колін, з’єднує резервуари A і B (рис. 1.29). Різниці рівнів ртуті у манометрі складають h1 = 200 мм, h2 = 250 мм, h3 = 300 мм, h = 700 мм. Густина ртуті рт 3 мρ = 13600 кг. Весь простір між рівнями ртуті у манометрі заповнений спиртом із густиною сп 3 мρ = 800 кг.
Визначити: а) абсолютний тиск повітря у резервуарі B, якщо манометричний тиск у резервуарі A дорівнює pA = 25 кПа; б) манометричний тиск у резервуарі A, якщо вакуум метричний тиск повітря у резервуарі B pвак = 35 кПа.
Задача 1.28. У циліндричний резервуар з діаметром D = 2 м до рівня H = 1,5 м налито бензин і воду (рис. 1.30). Густина бензину б 3 мρ = 750 кг, густина води б 3 мρ = 1000 кг . Рівень води у п’єзометрі нижче рівня бензину на h = 200 мм.
Визначити: а) вагу бензину, що перебуває у резервуарі; б) вагу води у резервуарі.
Задача 1.29. Визначити: а) абсолютний та вакуумметричний тиски на поверхні води у закритому резервуарі (рис. 1.31), якщо задані глибини h1 = 0,2 м, h2 = 0,3 м; б) глибину h1, якщо заданий абсолютний тиск на поверхні води у закритому резервуарі pабс = 80 кПа та pа = 100 кПа, h2 = 0,3 м.
Задача 1.30. До двох напірних трубопроводів A і B системи водопостачання підключений диференціальний ртутний манометр (рис. 1.32).
Визначити різницю тисків у трубопроводах, якщо: а) h1 = 400 мм, h2 = 650 мм; б) h1 = 380 мм, h2 = 820 мм; в) h1 = 200 мм, h2 = 700 мм.
Задача 1.31. Диференціальний манометр, що складається із двох колін, з’єднує резервуари A і B (рис. 1.33). Різниці рівнів ртуті у манометрі складають h1 = 200 мм, h2 = 250 мм, h = 700 мм. Густина ртуті рт 3 мρ = 13600 кг. Весь простір між рівнями ртуті у манометрі заповнений спиртом із густиною сп 3 мρ = 800 кг. Визначити: а) абсолютний тиск повітря у резервуарі B, якщо манометричний тиск у резервуарі A дорівнює pA = 25 кПа; б) манометричний тиск у резервуарі A, якщо вакуум метричний тиск повітря у резервуарі B pвак = 26,6 кПа.
Задача 1.32. У закритому резервуарі рівень нафти становить b = 0,8 м, рівень води a = 0,2 м (рис. 1.34). Густина нафти 3ρн = 850 кг м, густина води ρ = 1000 кг м3. Визначити: а) рівні h1 та h2, якщо абсолютний тиск на поверхні нафти у резервуаріp0 = 108 кПа , атмосферному тиску відповідає показання барометра hб = 750 мм рт.ст ; б) абсолютний тиск на поверхні нафти та рівень h2, якщо h1 = 2,0 м.
Задача 1.33. Відкритий кульовий резервуар (рис. 1.35) заповнений водою до половини свого об’єму за температури t°4oC. Як зміниться показання манометра pм при: а) підвищенні температури рідини; б) зниженні температури рідини. Випар рідини не враховувати.
Задача 1.34. Відкриті посудини, що сполучаються, заповнені водою(рис. 1.36). Як буде змінюватися рівень води у посудинах під час нагрівання: а) лівої посудини; б) правої посудини?1.35. Визначити різницю висот розташування об’єктів, якщо у першому з них густина атмосферного повітря ρ1, а у другому ρ2 :а) 1 3 мρ = 1,05 кг, 2 3 мρ = 0,95 кг; б) 1 3 мρ =1,15 кг, 2 3 мρ = 1,00 кг.
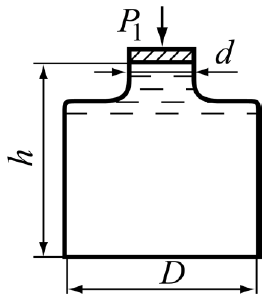
Приклад 1. Квадратний отвір з розмірами 1,5´1,5 м у боковій вертикальній стінці закритого резервуара закрито затвором (рис. 2.2). Визначити: силу тиску води на затвор, якщо горизонтальна основа 25 квадратного отвору розташована на глибині H = 3,0м, а манометричний тиск на вільній поверхні рідини pм = 40 кПа.
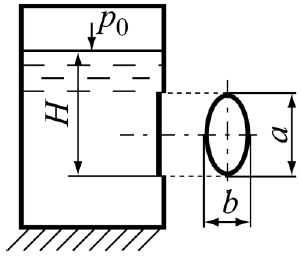
Приклад 2. У боковій стінці закритого резервуара є квадратний отвір із розмірами a ´ a = 0,5´0,5 м (рис. 2.3), геометричний напір над центром ваги отвору H = 0,5 м. Знайти величину й точку прикладання рівнодійної сили тиску бензину (б 3 мρ = 780 кг) на щит, що перекриває отвір, а також показати епюру тиску на нього, якщо абсолютний тиск на вільній поверхні бензину p0 = 80 кПа.
Задача 2.1. Поршень з діаметром d = 500 мм(рис. 2.4) має вагу G = 250 Н, глибина h = 0,8 м. Визначити: а) силу тиску на дно посудини, якщо діаметр її D = 1,0 м; б) вагу поршня G, якщо сила тиску на дно P = 8,0 кН.
Задача 2.2. Цистерна діаметром D, що герметично закрита,заповнена бензином (б 3 мρ = 750 кг) до висоти 2D (рис. 2.5) при манометричному тиску на поверхні pм. Визначити силу тиску на торцеву стінку та точку прикладання сили від дна цистерни x, якщо: а) D = 2,5 м, pм =15 кПа; б) D = 3,0 м, pм = 20 кПа.
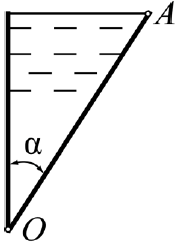
Задача 2.3. Визначити загальну силу тиску рідини на плоску стінку та побудувати епюру тиску на 1 м довжини стінки, що нахилена до горизонту під кутом α = 60o (рис. 2.6), якщо: а) глибини h1 = 4 м, h2 =1 м; б) h1 = 3 м, h2 = 0 м; в) h1 = 0 м, h2 = 4 м.
Задача 2.4. У закритому циліндричному резервуарі діаметром D = 2 м із бензином (б 3 мρ = 800 кг) відстоялася вода (рис. 2.7). Задані глибини H1 = 0,5м, H2 = 4 м. Визначити силу тиску на дно резервуара, якщо: а) манометричний тиск на поверхні резервуара pм =15 кПа; б) вакуум на поверхні резервуара pвак =15 кПа.
Задача 2.5. Гідросистема, що представлена на рисунку (рис. 2.8), застосовується для підйому вантажу G. Діаметри поршнів D = 300 мм, d =100 мм. Нехтуючи різницею висот, визначити: а) тиск у гідросистемі та вагу вантажу G, що розташований на поршні 2, якщо до поршня 1 прикладена сила F = 2 кН; б) силу F, що прикладена до поршня 1, якщо вага вантажу G = 20 кН.
Задача 2.6. На яку глибину необхідно опустити нижню кромку плоского затвора діаметром d = 0,8 м (рис. 2.9), щоб відстань між центром ваги C та центром тиску D, що виміряна по вертикалі, складала:а) d321; б) d161; в) 81d
Вартість: 50 грн (Варіант а, б)
Задача 2.7. Поршень вільно переміщується у циліндрі, що заповнений водою (рис. 2.10). Глибини H1 = 3м, H2 = 5м. Визначити: а) масу поршня, якщо діаметр його дорівнює d = 0,1м; б) діаметр поршня d, якщо маса його m = 25кг.
Задача 2.8. У боковій стінці закритого резервуара є отвір, що перекривається щитом у формі еліпса із розмірами a = 2,5 м, b = 1,5 м (рис. 2.11). Нижня кромка отвору занурена на глибину H = 3 м від рівня води. Визначити: силу гідростатичного тиску води на щит та знайти місце розташування центра тиску, якщо абсолютний тиск на вільній поверхні резервуара дорівнює: а) p0 = 110 кПа; б) p0 = 90 кПа; в) p0 = pa.
Вартість: 50 грн (Варіант а, б, в)
Задача 2.9. Циліндр (рис. 2.12) заповнений рідиною із густиноюм3ρ = 850 кг. До поршня діаметром 30d = 0,1 м, прикладена сила F = 200 Н. Визначити: а) показання манометра, якщо висота H = 1,7 м; б) висоту H, якщо показання манометра pм = 120 Па.
Задача 2.10. Прямокутний щит довжиною a = 5 м та шириною b = 5 м закріплений за допомогою шарніра в точці О (рис. 2.13). Глибини H1 = 4 м , H2 = 2 м. Визначити: а) силу T, яку необхідно прикласти для підйому щита; б) реакції опор А і О.
Вартість: 40 грн (Варіант а)
Задача 2.11. Відкритий резервуар шириною B (рис. 2.14) розподілений перегородкою на три відсіки, у яких містяться різні рідини: бензин (б 3 мρ = 850 кг), вода ( в 3 мρ = 1000 кг), мінеральне масло (м3мρ = 800 кг). Визначити: рівнодійні сил тиску рідин на перегородки I і II та точки їх прикладання, якщо: а) ширина бака B = 1,0 м, рівень рідин H = 2,5 м; б) B = 2 м, H = 2,0 м; в) B = 1,5 м, H = 2,5 м.
Вартість: 60 грн (Варіант б)
Задача 2.12. Цегляна стінка розподіляє резервуари з двома рівнями рідини (рис. 2.15). Висота стінки h = 3 м, ширина b = 1 м, довжина стінки у площині, що перпендикулярна до креслення, l = 6 м. Коефіцієнт тертя кладки об грунт f = 0,5, густина кладким 3ρ = 2400 кг. Перевірити остійність стінки на ковзання та перекидання, якщо: а) глибини h1 = 2,2 м, h2 = 0,8 м; б) h1 =1,8 м, h2 = 0,9 м; в) h1 = 3,0 м, h2 = 1,0 м.
Вартість: 100 грн (Варіант а, б, в)
Задача 2.13. У боковій вертикальній стінці закритого резервуара (рис. 2.16) круглий отвір з діаметром d = 0,5 м закритий кришкою. Нижня точка отвору розташована на глибині H = 1,7 м. Визначити силу тиску води на кришку та відстань точки прикладання цієї сили від п’єзометричної площини, якщо: а) манометричний тиск на вільній поверхні води дорівнює pм = 70 кПа; б) вакуум метричний тиск на поверхні води у резервуарі pвак = 5 кПа; в) на вільній поверхні води pм = 0.
Вартість: 50 грн (Варіант в)
Задача 2.14. Прямокутний щит шириною b = 1,2 м, при глибині H = 1,5 м і розмірі a = 0,3 м може обертатися навколо осі О (рис. 2.17). Нехтуючи вагою щита та силою тертя, визначити силу F, яку необхідно прикласти для підйому щита, якщо кут нахилу: а) α = 45o; б) α = 60o.
Вартість: 50 грн (Варіант а)
Задача 2.15. Три поршні з площами 2S1 = 0,05 м, 2S2 = 0,02 м, 2S3 = 0,01 м розташовані на поверхні води у циліндрах, що сполучаються (рис. 2.18). Визначити: а) величини x та y, якщо на поршні діють сили P1 = 200 Н, P2 = 150 Н, P3 = 100 Н; б) сили P1 та P2, якщо відомі величини x = 40см, y = 30 см, P3 = 80 Н.
Задача 2.16. Круглий отвір діаметром d =100 мм, що розташований у дні резервуара (рис. 2.19), закрито клапаном, діаметр якого D = 200 мм. При якому вакуумметричному тиску у резервуарі клапан почне пропускати воду, якщо:а) маса клапана m = 5 кг, H = 1,5 м; б) m = 10 кг, H = 1,0 м; в) m = 1,2 кг, H = 0,5 м.
Задача 2.17. Визначити: а) на яку висоту h може підняти воду паровий поршневий насос (рис. 2.20), якщо манометричний тиск у паровому циліндрі pм = 200 кПа, його діаметр D1 = 150 мм,діаметр водяного циліндра D2 = 200 мм; б) манометричний тиск у паровому циліндрі pм, якщо вода піднімається на висоту h = 10 мпри тих самих D1 і D2.
Задача 2.18. Визначити, при якому вакуумметричному тиску у закритому резервуарі (рис. 2.21) сила тиску на круглу кришку діаметром D = 1 м дорівнює нулю. Геометричний напір над центром ваги отвору H = 3 м. У резервуар налито: а) нафту ( 3 мρ = 850 кг); б) воду; в) бензин (3 мρ = 740 кг).
Задача 2.19. У резервуар налито ртуть, воду та масло (рис. 2.22). Висота шару ртуті h1, води h2, масла h3. Густина масла м 3 мρ = 800 кг, водив 3 мρ =1000 кг, ртуті рт 3 мρ = 13600 кг. Побудувати епюру манометричного тиску та визначити манометричний тиск на дно резервуара. Знайти силу тиску на бокову поверхню резервуара,якщо ширина її b при: а) h1 = 0,2 м, h2 = 0,5 м, h3 = 1,2 м,b = 1,5 м; б) h1 = 0,3 м, h2 = 0,8 м, h3 = 0,5 м, b = 2,2 м; в) h1 = 0,2 м, h2 = 0,6 м, h3 = 1,0 м, b = 2 м.
Задача 2.20. Герметично закрита бочка, що частково заповнена бензином із глибиною h, плаває у воді (рис. 2.23). Діаметр бочки D = 0,5 м, густина бензину б 3 мρ = 750 кг. Визначити силу тиску на дно бочки, якщо:а) H = 1,5 м, h =1,0 м, манометричний тиск на вільній поверхні бензину pм = 20 кПа, б) H = 1,3 м, h = 1,3 м,вакуум на поверхні бензину pвак = 10кПа.
Вартість: 40 грн (Варіант а)
Задача 2.21. У боковій стінці резервуара і з нафтою (н 3 мρ = 900 кг) є квадратний отвір a ´ a = 0,5´ 0,5 м (рис. 2.24). Визначити: а) величину 1 й точку прикладання рівнодійної сили тиску рідини на кришку, що закриває цей отвір, якщо напір H = 1,5 м, показання ртутного U–подібного манометра, який прикріплений до резервуара, h = 250 мм, атмосферний тиск pа = 100 кПа; б) при якому абсолютному тиску на вільній поверхні p0 кришка перебуватиме у рівновазі?
Вартість: 60 грн (Варіант а, б)
Задача 2.22. Система, що складається з двох поршнів (рис. 2.25), перебуває у рівновазі. Діаметр більшого поршня D = 300 мм, меншого d = 50 мм. Різниця рівнів h = 30 см. Трубки заповнені водою. Вагу поршнів не братидо уваги. Визначити: а) яку силу P235 необхідно прикласти до більшого поршня, якщо сила, що прикладена до малого поршня дорівнює P1 = 150 Н; б) силу P1, що прикладена до малого поршня при заданій силі P2 = 7 кН.
Задача 2.23. Визначити, при якому вакуумметричному тиску у закритому циліндричному резервуарі з діаметром D (рис. 2.26) сила тиску на дно дорівнює нулю, якщо задані: а) D =1,0 м, H1 = 0,2 м, H2 =1,5 м; б) D = 1,0м, H1 = 0,2 м, H2 = 2,0 м; в) D = 1,5 м, H1 = 0,5м, H2 = 1,0 м ; г) D = 1,0 м , H1 = 0,3 м, H2 = 2,0 м.
Задача 2.24. Рівнодійна сил тиску рідини R зліва та справа на вертикальну стінку розташована на рівні вільної поверхні рідини у другому резервуарі (рис. 2.27). Встановити співвідношення глибин h1 та h2 у резервуарах, що заповнені однаковою рідиною та знайти глибину h2, якщо: а) h1 =1 м; б) h1 = 1,5 м.
Задача 2.25. Відкрита посудина з масою m = 16 кг, що складається із двох частин з діаметрами D = 0,5 м і d = 0,3 м,заповнюється водою (рис. 2.28). Визначити: а) необхідний об’єм води у верхній частині посудини, при якому посудина буде підніматися над поршнем; б) за якої мінімальної маси посудини m вона не буде підніматися над поршнем, якщо об’єм води у верхній частині посудини W = 10 л?
Задача 2.26. Труба діаметром D = 400 мм з’єднана із трубою діаметром d = 50 мм, як показано на рисунку (рис. 2.29). Висота стовпа води h = 80 см. В трубах розміщені поршні. Визначити: а) силу P2, яку треба прикласти до поршнів А і В, щоб система знаходилася у рівновазі, якщо на поршень С діє сила P1 = 98,1 Н; б) силу P1, якщо сила P2 = 8,0 кН.
Задача 2.27. Нахилений щит має можливість обертатися навколо шарнірної осі O (рис. 2.30). Рівень води з правого боку від щита h = 0,5м. Відстань від шарніра до низу щитаx = 1,35 м. Нехтуючи вагою щита та тертяму шарнірі, визначити глибину H, при якій буде відбуватися автоматичне відкриття щита, якщо кут нахилу: а) α = 45o; б) α = 60o.
Задача 2.28. Циліндричний резервуар висотою h = 2,0 м і діаметром D = 1,0 м заповнений водою (рис. 2.31). У трубці, що приєднана до резервуара,рівень H. Визначити: а) сили, що розривають резервуар по перерізах1-1 і 2 — 2, та їх відстань від дна резервуара, якщо рівень води H = 15 м; б) рівень води H, якщо сила, що розриває резервуар по перерізу 1-1, дорівнює P1 = 130 кН.
Задача 2.29. Порожній, відкритий знизу,поршень (рис. 2.32) перебуває у рівновазі,якщо H = 6 h. Нехтуючи вагою поршня,визначити: а) діаметр D, якщо d = 50 мм; б) діаметр d, якщо D = 300 мм.
Задача 2.30. У двох циліндрах разом і з відповідними п’єзометрами перебувають однакові об’єми води (рис. 2.33). Кожний об’єм дорівнює об’єму п’єзометра висотою 40r. Визначити різницю рівнів води у п’єзометрах z, якщо система перебуває у стані рівноваги та: а) r = 0,2 м; б) r = 0,1 м.
Задача 2.31. Кубічний бак розподілений на дві рівні частини внутрішньою перегородкою (рис. 2.34). Обидві частини бака заповнені водою до рівнів H1 = 0,7 м та H2. Відомі показання манометра M, ртутного вакуумметра hрт, розміри a, b. Визначити силу, що діє на дно бака та реакції опор A і B, якщо: а) M = 30 кПа, hрт = 73,5 мм, H2 =1 м, a = 1,2 м, b =10 см; б) M = 20 кПа, hрт = 76 мм, H2 =1,2 м, a = 0,8 м, b =15 см; в) M = 35 кПа, hрт = 70 мм, H2 = 0,9 м, a = 1,0 м; b = 20 см. Вагою бака та вимірювальних пристроїв знехтувати.
Задача 2.32. Між вертикальною стінкою та стінкою AO, що нахилена від вертикалі під кутом α, знаходиться рідина з густиною ρ і вагою G (рис. 2.35). Ширина резервуара b =1,5 м. Визначити: а) силу тиску рідини на стінку AO та її момент відносно осі O, якщо α = 50o, 3 мρ = 900 кг, G = 7000H; б) теж саме при α = 75o, 3 мρ = 950 кг, G = 8000 H; в) при якому куті α момент сили тиску рідини на стінку буде мінімальним та якою тоді буде його величина, якщо 3 мρ =1000кг, G = 7500 H?Вказівка. Силу тиску та її момент треба визначати за допомогою величин G, b, α.
Задача 2.33. В диференціальному акумуляторі поршні з діаметрами D і d жорстко зв’язані між собою, а у простір між поршнями подається пара з абсолютним тиском p1 , внаслідок чого в нагнітальній трубі встановлюється манометричний тиск p і рухається поршень з діаметром dп (рис. 2.36). Визначити: а) необхідне значення p1, якщо D = 300мм, d = 200мм, dп =100мм, p = 150 кПа; б) який встановиться тиск p, якщо D = 200мм, d = 100мм, dп = 70мм, p1 = 150кПа; в) необхідне значення D, якщо d =120мм, dп = 80мм,p1 = 160кПа, p = 100 кПа; г) необхідне значення d, якщо D = 250мм , dп = 70мм, p1 = 150кПа, p = 255кПа. Вказівка. Сила тиску на поршень у нагнітальній трубі з діаметром dп врівноважується силами тиску на поршні з діаметрами d і D.
Задача 2.34. Лоток параболічного перерізу перекривається затвором того ж самого профілю (рис. 2.37). Визначити силу тиску на затвор та її точку прикладання при глибині води h і ширині по верху B = 2 ph (де p – параметр параболи), якщо: а) h = 0,8 м, p = 0,35 м; б) h = 0,95 м, p = 0,45 м; в) h = 0,75 м, p = 0,4 м.
Задача 2.35. Резервуар з прямокутним дном (рис.2.38) з розмірами l ´b при куті нахилу бокових стінок α заповнений водою до глибини h. Визначити: сили тиску на передню й бокові стінки резервуара і координати їх центрів тиску, якщо: а) l = 4 м, b = 2 м, l =1,9 м,α = 60o; б) l = 5 м, b = 2,5 м, h = 2,1м, α = 65o; в) l = 3,5 м, b = 2,2 м, l = 2,3 м, α = 70o.
Задача 2.36. Визначити сили тиску води на трикутні стінки резервуара (рис. 2.39) в положеннях m і n при: а) h = 0,7 м, l = 0,8 м, b =1,5 м; б) h = 0,55 м, l = 0,75 м, b = 1,45 м.
Задача 2.37. Лоток сегментного перерізу перекривається затвором того ж самого профілю (рис. 2.40). Визначити: силу тиску води на затвор і точку її прикладання при радіусі перерізу r і глибині води h, якщо: а) h = 0,6 м, r = 0,75 м; б) h = 0,55 м, r = 0,8 м; в) h = 0,35 м, r = 0,45 м.
Приклад 1. Визначити силу тиску води на криволінійну частину споруди a — b шириною b = 2 м при глибині води H = 1,2 м,манометричному тиску на поверхні pм = 2,9 кПа, радіусі r = 0,5 м (рис. 3.7).
Приклад 2. Визначити силу тиску рідини з густиною 3ρ = 900 кг, що відриває конусоподібний затвор від стінки, яка нахилена під кутом β = 30o (рис. 3.8), якщо l = 5 см, d = 4 см, a = 40 см.
Приклад 3. Визначити величину, точку прикладання і напрямок сили тиску води на 1 м ширини секторного затвора з радіусом R = 2м, якщо α = 30о(рис. 3.9).
Приклад 4. Визначити силу тиску рідини (м3ρ = 900 кг) Р1, що відриває сегментну кришку висотою h = 0,3 м від вертикального циліндра з висотою H = 2 м і діаметром D = 1 м, якщо на поршень з площею перерізу 2ωп = 20 см діє сила Р2 = 100 Н(рис. 3.10).
Задача 3.1. Побудувати тіла тиску для криволінійних поверхонь, що показані на рисунках (рис. 3.11).
Задача 3.2. Побудувати тіла тиску для криволінійних поверхонь, що показані на рисунках (рис. 3.12).
Вартість: 50 грн
Задача 3.3. Циліндричний затвор з діаметром D і довжиною l = 4 м перекриває випуск води з водосховища до каналу з глибиною h1 (рис. 3.13). Визначити силу тиску води на затвор, її напрямок і точку прикладання,якщо: а) D = 1,2 м, h1 = 0,4 м; б) D = 1,0 м , h1 = 0,6 м; в) D = 1,4 м, h1 = 0,7м.
Задача 3.4. Кульовий клапан діаметром D і масою M, що занурений у воду, закриває вхід у трубу діаметром d (рис. 3.14). Рівень води в трубі на величину h вище рівня у резервуарі. Визначити: а) при якому значенні h клапан почне пропускати воду з труби, якщо D = 150 мм, d =100 мм, M = 0,05 кг; б) при якому діаметрі клапана D вода почне витікати з труби, якщо d = 90 мм, M = 0,04 кг, h =16 см; в) при якій масі M клапан закриє вхід у трубу, якщо d = 93 мм, h = 18,5 см, D = 135 мм; г) при якому діаметрі труби d клапан закриє вхід до неї, якщо h =17 см, D = 130 мм, M = 0,035 кг.
Задача 3.5. Сталева (3 мρ= 7800 кг) куля радіусом R перекриває отвір у вертикальній стінці діаметром d = nR і перебуває у воді в стані рівноваги (рис. 3.15). Визначити: а) найменшу глибину занурення центра кулі H при R = 100 мм іn = 1,5; б) найменший радіус кулі R при n = 1,7 і глибині H = 1,0 м; в) найменший діаметр отвору d при n = 1,25 і глибині H = 2,2 м.
Задача 3.6. Отвір у вертикальній стінці резервуара з глибиною h1 = 1,3 м перекривається кульовим клапаном з діаметром D (рис. 3.16). Глибина справа h2. Визначити силу тиску води P на клапан та її напрямок, якщо: а) D = 0,4 м, h2 = 0,2 м; б) D = 0,6 м, h2 = 0,25 м; в) D = 0,7 м, h2 = 0,4м.
Вартість: 60 грн (Варіант а)
Задача 3.7. Визначити силу тиску R на упор, що підтримує вигін труби(рис. 3.17) діаметром d при повороті на кут α і тиску в трубі p, якщо: а) d = 400 мм, p = 400 кПа, α = 45o; б) d = 300 мм, p = 343 кПа, α = 60o; в) d = 250 мм, p = 300 кПа, α = 30o.
Задача 3.8. Визначити силу тиску води на секторний затвор (рис.3. 18), її напрямок і точку прикладання, якщо: а) глибина води H = 4 м, радіус затвора R = 0,9 м, ширина b = 3 м; б) H = 3 м, R = 0,8 м, b = 4 м; в) H = 2 м, R = 1 м, b = 2,5 м.
Вартість: 40 грн (Варіант б, в)
Задача 3.9. Побудувати тіло тиску рідини для криволінійної фігури ABCDE (рис. 3.19).
Задача 3.10. Конічна кришка з діаметром d і висотою l закріплена болтами до стінки закритого резервуара на висоті h від дна, до якого приєднаний манометр з показником M (рис. 3.20). Рівень рідини з густиною ρ над віссю кришки H, маса кришки m. Визначити абсолютний тиск p0 на поверхні рідини у резервуарі та сили, що намагаються відірвати та зрізати болти, якщо: а) d = 0,7 м, l = 0,6м, h =1 м, H = 1,5 м, M = 10 кПа, 3 мρ = 1000 кг, m = 10кг; б) d = 0,6м, l = 0,6м, h = 0,8 м, H = 0,5 м, M = 15 кПа, м3ρ = 900 кг, m = 9кг; в) d = 0,5 м, l = 0,4 м, h = 1,2 м,H = 0,4 м, M = 8кПа, 3 мρ = 800 кг, m = 8 кг.
Задача 3.11. У прямокутному куті посудини, що заповнена рідиною з густиною ρ до глибини h = 3 м, розташована 81 частина кулі з радіусом r (рис. 3.21). Визначити: а) рівнодійну силу тиску на її поверхню та кути між нею та осями x, y, z (вісь y перпендикулярна до креслення у точці А), якщо r = 1,5 м, 53м3ρ = 1000 кг; б) густину рідини, якщо при r = 1 м рівнодійна сили тиску на криволінійну поверхню P = 30 кН.
Задача 3.12. Визначити величину,напрямок і точку прикладання сили тиску води на секторний затвор при ширині b, радіусі R, кутах α і β (рис. 3.22), якщо: а) b = 3м, R = 3м, α = 50o, β = 35o; б) b = 4м, R = 3,5м, α = 40о, β = 30о; в) b = 5м, R = 4м, α = 35o, β = 22о.
Вартість: 60 грн (Варіант а, в)
Задача 3.13. Вода налита у відкритий зверху та знизу усічений конус, який встановлено на гладкій горизонтальній підставці без зазорів між нею та конусом (рис. 3.23). Розміри конуса R = 40 см, r = 20см, h = 60см. Визначити: а) при якій глибині z і масі M = 100 кг конус буде підніматися, а вода буде витікати з-під нього? б) при якій мінімальній масі конуса він не буде підніматися, а рідина не буде витікати з-під нього, якщо глибина z = 40 см?
Задача 3.14. Кульова посудина з радіусом R заповнена рідиною з густиною ρ та підвішена за допомогою ланцюга до стелі (рис. 3.24). Показник пружинного вакуумметра pвак , вага нижньої половини посудини G. Визначити умови, за яких нижня половина посудини не буде відриватися від верхньої, тобто: а) знайти pвак при R = 400мм, 3 мρ = 900кг, G = 1500H; б) знайти R при 3 мρ = 880 кг, G = 1000H, 10 кПа pвак = ; в) знайти G при 3 мρ =1100 кг, R = 350 мм, 8,5 кПа pвак = ; г) знайти ρ при G = 600H, R = 500мм, pвак = 8 кПа.
Задача 3.15. У робочій камері поршневого насоса при зворотньо-поступальному русі поршня у циліндрі з діаметром D = 110 мм утворюється вакуум або манометричний тиск (рис. 3.25). У нижній і верхній стінках камери є отвори з діаметрами d, які перекриваються кульовими сталевими = ст 3 мρ 7800 кг клапанами з радіусами R. Вісь циліндра знаходиться вище нижнього отвору на величину h1 і на таку ж величину нижче верхнього отвору, а нижня стінка камери розташована вище поверхні у резервуарі на величину h2 . На відстані h3 над верхньою стінкою камери вода подається по трубі до споживача. Визначити сили, що необхідно прикласти до штоку циліндра для відкриття нижнього Pшн та верхнього клапана Pшв, якщо: а) R = 90 мм, d =100 мм, h1 = 0,45м, h2 = 5,5 м, h3 = 2,5 м; б) R = 80 мм, d = 90 мм, h1 = 0,4м, h2 = 6,5 м, h3 = 3,8 м; в) R = 70мм ,d = 80 мм, h1 = 0,5 м, h2 = 7 м, h3 = 3 м.
Задача 3.16. Круговий отвір у дні резервуара закритий кульовим клапаном діаметром 2rі масою M (рис. 3.26). Діаметр отвору r = 10 см, глибина води у резервуарі h = nr, абсолютний тиск на поверхні p0. Визначити: а) силу, що необхідна длявідкриття клапана, якщо M = 1 кг, n = 3, p0 = 102305 Па; б) масу клапана, якщодля відкриття його при n = 5 і p0 = 99362 Па необхідно прикласти силу G = 9,5 Н; в) відношення rn = h, якщо для відкриття клапана з масою M = 0,8 кг, при p0 = 101, 325 кПа треба прикласти силу G = 50 Н.
Задача 3.17. Кульовий резервуар з радіусом Rі масою m закріплений на фундаменті та заповнений водою наполовину (рис. 3.27), тиск газу у ньому p. Фланцеві з’єднання частин резервуара знаходяться у площині, що має нахил до горизонту під кутом α. Визначити сили, що зрізують і розривають ці з’єднання, якщо: а) α = 90o, R = 0,35м, m = 300 кг, p = 20 кПа; б) α = 45o, R = 0,4м, m = 250 кг, p = 18 кПа; в) α = 30o, R = 0,5 м, m = 200кг, p = 25 кПа; г) α = 0o,R = 0,45 м, m = 280 кг, p = 22 кПа.
Задача 3.18. Сегментний затвор шириною b = 2 м, радіусом r і кутом α встановлений на водозливі (рис. 3.28). Визначити силу тиску на затвор, кут її нахилу до осі 0x й точку прикладання сили (координати x і z), вважаючи, що рівень води співпадає з верхньою кромкою затвора, якщо: а) α = 60о, r = 3,5 м; б) α = 45о, r = 3,0 м; в) α = 30o, r = 2,5м.
Задача 3.19. На дні закритої посудини встановлена чверть круглого циліндра довжиною l =1 м з радіусом r (рис. 3.29). Глибина води у резервуарі h, абсолютний тиск на поверхні p0. Визначити силу тиску води на криволінійну поверхню та її напрямок, якщо: а) h = 20 см, r = 60 мм, p0 = 105 кПа; б) h = 30 см, r = 50мм, p0 = 99,5кПа; в) h = 50 см, r = 80 мм, p0 = 103,5 кПа.
Вартість: 50 грн (Варіант в)
Задача 3.20. Циліндричний затвор діаметром D = 20 см і довжиною l = 50 см розділяє дві посудини(рис. 3.30). Визначити загальну силу тиску рідини на затвор та її напрямок, якщо: а) глибина зліва h = 40 см, справа h1 =15 см, абсолютний тиск на поверхні рідини p0 = 105 кПа, густина рідини 3 мρ = 850 кг; б) h = 30 см, 8см h1 = , p0 = 95 кПа, м3ρ = 950кг; в) h = 35 см, 10 см h1 = , p0 = 99,35 кПа, м3ρ =1000 кг.
Вартість: 60 грн (Варіант а, б)
Задача 3.21. Лоток шириною b заповнений водою до глибини h (рис. 3.31). У нижній частині бокові стінки лотка окреслені по колу радіусом r. Визначити рівнодійні сил тиску води на криволінійну частину поверхні DE і на всю поверхню BCDE, а також точки їх прикладання, якщо: а) b = 0,8 м, h = 0,6 м, r = 0,3 м; б) b = 0,9 м, h = 0,8 м, r = 0,25 м; в) b = 0,7 м, h = 0,55 м, r = 0,2 м. Розрахунок провести на 1м довжини каналу.
Задача 3.22. Циліндричний порожній затвор діаметром D з діаметром опорного кільця d , перекриває прогін водозабірної споруди b (рис. 3.32). Циліндр при підйомі може перекочуватися по нахилених рейках A-B, що розміщені під кутом α до дна каналу і спираються на опори у точках A на дні і B на відстані l = 1,5 м від дна. Визначити силу тиску води P на затвор, що опущений на дно,величини реакцій опор RA і RB, якщо маса затвору m , глибини води h1 = D і h2 при: а) D = 1,2 м, d =1,0 м, h2 = 0,7м, b = 5 м, α = 70о, m = 1000 кг; б) D = 1,5 м, d =1,05 м, 0,75 м h2 = , b = 6 м; α = 72о, m = 1200 кг; в) D = 1,0 м, d = 0,8 м, 0,4 м h2 = , b = 4 м, α = 65о, m = 900 кг.
Задача 3.23. До півкулі d = 4,0 м приєднана відкрита вертикальна трубка, вся система заповнена водою (рис. 3.33). Визначити: а) при якій масі півкулі m вона буде відриватися по лінії M – M, якщо h = 4,0м; б) силу, що необхідна для відриву півкулі по лінії M – M при h = 1,8 м і масі півкулі m = 10000 кг; в) при якій висоті рівня води у трубці h півкуля буде відриватися по лінії M – M, якщо її маса m = 13000 кг.
Задача 3.24. Для прочищення самопливного водовідвідного трубопроводу діаметром d використовується порожня металева куля діаметром d nd к = , яка притискається до верхнього півкола труби(рис. 3.34), в наслідок чого в колодязі створюється підпір води H над верхом труби, а осад змивається струменем води, що витікає з-під кулі. Визначити силу P, що необхідно прикласти до кулі, щоб утримати її у призначеному місці, якщо: а) d = 600 мм, H = 2,0 м, n = 0,85; б) d = 550 мм, H = 2,1 м, n = 0,8; в) d = 450 мм, H = 1,8 м, n = 0,75.
Задача 3.25. Визначити кути нахилу та сили тиску води на плоску та напівсферичну стінки циліндричної посудині (рис. 3.35) діаметром D при показниках манометра z = nD, якщо: а) n = +0,2, D = 100 см; б) n = +0,25, D = 80 см; в) n = -0,5, D = 110 см; д) n = -0,3, D = 120 см.
Задача 3.26. У куті резервуара α з горизонтальним дном і вертикальними стінками розташована частина півкулі з радіусом r (рис. 3.36). Глибина води H. Визначити силу тиску води на тіло та її напрямок, якщо: а) α = 65o, r = 1 м, H = 2м;б) α = 130o, r = 1,2м, H = 2,5м; в) α = 40o, r = 1,3м, H = 1,5 м. Вказівка. Для визначення горизонтальної проекції сили необхідно знайти проекцію частини півкулі та її центр ваги.
Приклад 1. Рідина із густиною 3 мρ = 800 кг перебуває у відкритому прямокутному резервуарі довжиною l = 10 м, шириною b = 2 м, висотою a = 1,6 м при глибині h0 =1,2 м. Визначити: а) які глибини встановляться біля лівої і правої стінок резервуара і які сили будуть діяти на ці стінки, якщо резервуар рухатиметься по горизонтальному шляху (рис. 4.11, а) з прискореннямс 2j = 0,7 м; б) при якому максимальному прискоренні j max рідина не буде виливатися із резервуара, якщо кут нахилу шляху α = 3,5o (рис. 4.11, б), а також якими будуть максимальні сили тиску на бічні стінки.
Приклад 2. Рідина заповнює частину відкритого циліндричного резервуара діаметром D = 1 м і висотою H = 0,8 м (рис. 4.13). Визначити кутову швидкість обертання W¢, при якій поверхня рідини торкнеться дна, а також кутову швидкість W¢¢, при якій рідина почне виливатися з резервуара. Крім того, знайти кількість рідини, що залишиться у резервуарі при торканні поверхнею обертання дна, якщо на початку обертання він заповнений на: а) 65%; б) 35%.
Задача 4.1. На транспортному засобі, що рухається горизонтально з прискоренням j, встановлена U — подібна трубка малого діаметра,що заповнена рідиною = м3ρ 900 кг з відстанню між її гілками lі різницею рівнів рідини у гілках h (рис. 4.14). Визначити: а) з яким прискоренням j рухається засіб, якщо h = 5см, l = 30см; б) якою буде різниця рівнів h, якщо с2j = 1,9 м, l = 40 см; в) значення h при l = 35см, якщо за 10 с швидкість рівномірно зменшувалася відгод60 км догод 45 км.
Задача 4.2. Призматичний резервуар, що розподілений перегородкою на дві частини з довжинами l1 = 2м, l2 = 1 м і шириною b = 2 м, заповнений водою з глибинами h1 і h2 = 1,75 м та рухається горизонтально з прискоренням j (рис. 4.15). Внаслідок цього на перегородку діє загальна сила тиску P. Визначити: а) значення P та її напрямок, якщо с2j = 4 м, 1м h1 = ; б) прискорення j, якщо h1 = 1,1м, P = 0 кН; в) глибину біля лівої стінки h1, якщо с2j = 3,5 м і P = 2,2 кН. Вказівка. Напрямок сили вправо вважати додатним.
Задача 4.3. Визначити горизонтальне прискорення резервуара з рідиною (рис. 4.15), при якому повністю розвантажується перегородка між його частинами, довжини яких l1, l2 = 1,5 м і глибини у резервуарах відповідно h1 і h2, якщо: а) l1 = 2 м, h1 = 1,2 м і h2 = 1,4м; б) l1 =1,8 м, h1 = 1,6 м, h2 = 2 м; в) l1 = 2,8 м, h1 = 1,8 м, h2 = 2,4м.
Задача 4.4. Резервуар з масою M = 90 кг, діаметром D = 0,8 м, що заповнений рідиною = м3ρ 850 кг до глибини h = 1 м, піднімається догори з прискоренням j (рис. 4.16). Визначити: а) силу тиску рідини на дно резервуара, якщо с2j = 2 м; б) прискорення j, якщо при підйомі резервуара треба було прикласти силу P = 6,5 кН.
Задача 4.5. Тор із зовнішнім радіусом R = 0,5 м, що заповнений ртуттю до рівня h = nR, рухається горизонтально з прискоренням j (рис. 4.17). Визначити: показник манометра Mу найнижчій точці тора, якщо: а) n = 0,7, j = g; б) n =1, с2j = 2 м; в) n = 1,5, с2j = 5 м.
Задача 4.6. Цистерна діаметром D = 1,2 м і довжиною l = 5 м заповнена нафтою (м3ρ = 850 кг) до відмітки над віссю H = 1 м і рухається горизонтально з прискоренням j (рис. 4.18). Визначити: а) сили тиску нафти на плоскі бокові стінки цистерни A і B та відстань D від точки їх прикладання до центра стінки при с2j = 1,4 м; б) при якому прискоренні j сила тиску на праву плоску стінку буде у двічі більша, ніж на ліву; в) сили тиску, що відривають бічні сферичні(замість плоских) стінки цистерни A і B, якщо висоти кульових сегментів h = 0,3 м, а с2j = 1,2 м.
Задача 4.7. Посудина у вигляді паралелепіпеда довжиною l = 0,8 м, шириною b = 0,4 м, висотою H, що заповнена рідиною до глибини h,рухається по горизонтальній поверхні з прискоренням j (рис. 4.19). Визначити: а) прискорення j, при якому з посудини виллється третина рідини, якщо H = 0,8 м, h = 0,6 м; б) висоту H, при якій рідина не буде виливатися з посудини, якщо h = 0,55 м, с2j = 2м.
Задача 4.8. Цистерна, що заповнена рідиною, рухається по шляху з похилом i з прискоренням j (рис. 4.20). Діаметр її горловини d = 0,7 м, висота над поверхнею нафти у нерухомій цистерні при її горизонтальному положенні D. Визначити: допустимі умови (значення j або i), при яких нафта не буде переливатися через край горловини,якщо: а) i = 0,1, D=0,2 м, б) j= 3 м/с, D= 0,1 м. Вказівка: Похил i = sinα.
Задача 4.9. У відкриту циліндричну посудину з висотою H = 0,8 м та діаметром D = 0,6 м налито 0,16 м3 води. Посудина обертається навколо вертикальної осі. Визначити: а) який об’єм води залишиться у посудині і якою буде відмітка найнижчої точки поверхні обертання, якщо кутова швидкість W=15 c-1; б) при якій кількості обертів за хвилину поверхня обертання доторкнеться дна посудини і який, у цьому випадку, в ній залишиться об’єм води; в) при якій кутовій швидкості об’єм води у посудині зменшиться втричі і де буде нижня точка параболоїда обертання.
Задача 4.10. Півкуля з радіусом r була заповнена доверху водою (рис. 4.21) та оберталася з кутовою швидкістю W навколо вертикальної осі, в наслідок чого рідина переливалася через край. Після припинення обертання у півкулі встановилася глибина h. Визначити: а) якою була кутова швидкість обертання, якщо r = 0,6 м, h = 0,25 м; б) об’єм, що залишиться у півкулі, і глибину h, якщо r = 0,45 м, W= 5 с-1; в) якою була кількість обертів півкулі за хвилину n , якщо при r = 0,7 м встановилася глибина h = 0,4 м; г) скільки рідини переллється через край і яка глибина встановиться у півкулі після припинення обертання, якщо r = 0,8 м, кількість обертів за хвилину n = 35.
Задача 4.11. Посудина у формі півкулі з радіусом r = 0,5 м наповнена до верху рідиною та обертається навколо вертикальної осі, що проходить через центр (рис. 4.21). Визначити: а) при якій кількості обертів n за хвилину вільна поверхня доторкнеться дна півкулі і який об’єм рідини виллється з неї; б) якою була кутова швидкість W, якщо після припинення обертання глибина зменшилася удвічі, і скільки рідини залишилося у посудині.
Задача 4.12. Бензин подається з бензобака автомобіля до карбюратора по трубопроводу малого діаметра, вхід до якого занурений у бензині знаходиться на відстані h від дна бака. Довжина бака L = 55 см, ширина b = 18 см, висота H = 22 см (рис. 4.22). При русі автомобіля з прискоренням j у баку має залишатися мінімальний об’єм пального Wmin. Визначити: а) необхідне значення h, якщо Wmin = 2,5 л, а автомобіль починає рух і за 10 с набирає швидкість год V = 100 км; б) максимальне прискорення автомобіля j, якщо Wmin = 2 л, h = 10 мм; в) мінімальний об’єм пального у баку Wmin, якщо h = 13 мм, с2j = 3,5 м.
Задача 4.13. До кузова автомобіля-самоскида, що рухається зі швидкістю V, налито цементного розчину = м3ρ 1900 кг при глибині h (рис. 4.23). Параметри автомобіля:відстань між осями l1 = 4,5 м, відстань від задньої осі до заднього борту l2 = 1,2 м, довжина кузова l = 3,5 м, ширина b = 1,8 м і висота H = 0,7 м, вага порожнього автомобіля G = 15 кН розподіляється між осями як 1:1. Визначити за умови не виливання розчину із кузова:а) мінімальний час tг і довжину Sг рівномірного гальмування, сили ваги на передню й задню осі, якщо h = 0,5 м,год V = 36 км; б) максимальну швидкість V, довжину г S рівномірного гальмування г S, сили ваги на передню й задню осі, якщо h = 0,55 м, час рівномірного гальмування tг = 10с.
Задача 4.14. Закритий кузов причепу автомобіля з розмірами l = 4 м, b = 1,8 м, H і відстанню між колесами вздовж осі b1 заповнений бетонним розчином = б 3 мρ 2400 кг до глибини h (рис. 4.24). Автомобіль рухається на повороті шляху вправо з радіусом R = 25 м із швидкістю V. При рівномірному русі без розчину навантаження на кожне з чотирьох коліс G = 5 кН. Визначити положення поверхні розчину і вертикальні навантаження на колеса, якщо: а) H = 1,25 м, год V = 40 км, h = 1 м, b1 = 1,4 м; б) H = 1,4 м, год V = 20 км, h = 1,1 м, b1 = 1,3 м. Вказівка. Попередньо необхідно визначити, чи буде вільна поверхня розчину торкатися кришки причепу.
Задача 4.15. Закрита циліндрична коробка з радіусом R = 50 см і висотою H = 45 см заповнена рідиною до глибини h = 30 см (рис. 4.25). Визначити, з якою кутовою швидкістю має обертатися коробка навколо своєї вертикальної осі, щоб: а) нижня точка поверхні обертання торкалася дна, і де в такому випадку буде розташована верхня її точка; б) поверхня обертання торкалася кришки коробки і де тоді буде її нижня точка.
Задача 4.16. Півкуля з радіусом R заповнена водою до глибини h = 0,8 R і обертається навколо вертикальної осі з n обертами за хвилину (рис. 4.26). Визначити, скільки рідини переллється через край і яка глибина встановиться у півкулі після припинення обертання, якщо: а) R = 0,5 м, n = 40; б) R = 0,7 м, n = 35;в) R = 0,6 м, n = 50.
Задача 4.17. У відкритий зверху циліндричний резервуар з висотою H = 0,7 м і радіусом R = 0,5 м налито рідину (м3ρ = 800 кг) до глибини h = 0,5 м. Визначити: а) з якою кутовою швидкістю W резервуар має обертатися навколо вертикальної осі для того, щоб з нього витекло 35% від початкового об’єму; б) як зміниться сила тиску рідини на дно резервуара при кількості обертів за хвилину n = 80; в) при якій максимальній кутовій швидкості W рідина не буде виливатися із резервуара.
Задача 4.18. Посудина, що складається з двох циліндрів з діаметрами D = 0,4 м і d = 0,2 м, висотами H і h = 0,3 м обертається навколо вертикальної осі (рис. 4.27). Нижній циліндр до початку обертання був вщерть заповнений рідиною. Визначити: а) кутову швидкість, при якій поверхня обертання торкнеться дна посудини, якщо при H = 0,3 м рідина не буде виливатися з верхнього циліндра, та який об’єм рідини залишиться у нижньому циліндрі; б) при якій висоті верхнього циліндра H поверхня обертання досягне його краю і водночас торкнеться дна нижнього циліндра та який об’єм рідини перетече до верхнього циліндра, якщо кутова швидкість W=15 с-1; в) при якій кількості обертів за хвилину об’єми рідини в обох циліндрах зрівняються і якого рівня hв¢ досягне поверхня обертання у верхньому циліндрі.
Задача 4.19. Водяний мановакуумметр з радіусами гілок R1 = 15 см і R2 = 20 см приєднаний до закритої посудини, що заповнена газом під абсолютним тиском p0 (рис. 4.28). Визначити: а) показання мановакуумметра h, якщо p0 = 100 кПа і посудина рухається вертикально до гори і донизу з прискоренням 2 сj = 1,5 м; б) прискорення вертикального руху донизу j, якщо p0 = 101 кПа, h = 50 мм; в) кількість обертів посудини за хвилину n навколо вертикальної осі, якщо показання мановакуумметра h = +10 см, p0 = 101,324 кПа; г) показання мановакуумметра h, якщо p0 = 103 кПа, а посудина обертається навколо вертикальної осі з кутовою швидкістю W = 10 с-1. Вказівка. Залежно від умов задачі висота h може бути додатна (у трубці з радіусом R2 більше, ніж у трубці з радіусом R1) або від’ємна, якщо навпаки.
Задача 4.20. Циліндрична посудина з висотою H і діаметром D = 0,7 м заповнена водою до глибини h і обертається навколо вертикальної осі з n обертами за хвилину (рис. 4.29). Визначити, при якому значенні n: а) об’єм води у посудині зменшиться вдвічі,якщо H = 0,5 м, h = 0,3 м; б) поверхня води торкнеться дна посудини, і який об’єм води при цьому витече з неї, якщо H = 0,45 м, h = 0,35 м.
Задача 4.21. Закритий циліндричний резервуар радіусом R1 = 0,5 м і висотою a вщерть заповнений рідиною з густиною 3 мρ = 800 кг і перебуває під тиском, який до початку обертання характеризує показник п’єзометра h, що встановлений на відстані R2 від осі резервуара (рис. 4.30). Резервуар приводиться до обертання з кутовою швидкістю W. Побудувати параболоїд обертання і визначити тиск p¢ у центрі верхньої кришки, силу тиску на кришку, тиск p¢ на дні біля бокової стінки резервуара, силу тиску на дно, якщо: а) R2 = 0,2 м, h = 280 мм, a = 0,6 м, W = 3,5 c-1; б) 0,3 м R2 = , h = 120 мм, a = 0,5 м, W = 7 c-1.
Задача 4.22. Резервуар висотою H = 1 м, діаметром D = 0,5 м з кришкою, що має форму кульового сегмента з висотою h = 0,2 м (рис. 4.31), вщерть заповнений водою та обертається навколо вертикальної осі з кутовою швидкістю W. У верхній точці кришки є малий отвір. Визначити: а) сили тиску на кришку Pкр та дно Рд резервуара, якщо W=10 c-1; б) кількість обертів за хвилину n, якщо сила тиску на кришку Pкр = 1 кН; в) кутову швидкістю W, якщо сила тиску на дно Pд = 3 кН.
Задача 4.23. Рідина (м3ρ = 850кг) заповнює горизонтальний циліндричний резервуар з діаметром D, який обертається навколо своєї осі при тиску на осі циліндра p0, і на його поверхні p (рис. 4.32). Визначити: а) тиск у верхніх точках резервуара p, якщо D = 1 м, W=10с-1, 5 кПа p0 = ; б) кутову швидкість W, якщо D = 900 мм, p = 8 кПа, p0 = 4 кПа; в) зусилля, що розривають циліндр, якщо його довжина l = 2 м, D = 110 см, W = 12c-1, 5,5 кПа p0 = .
Задача 4.24. Циліндрична посудина з діаметром D1 = 1 м і отвором у кришці діаметром D2 має висоту H = 0,8 м та наповнена до глибини h рідиною з густиною 3 мρ = 850 кг. Посудина обертається навколо вертикальної осі з кутовою швидкістю W (рис. 4.33). Визначити: а) кутову швидкість W, при якій рідина почне виливатися з посудині, якщо D2 = 0,6D1, h = 0,55 м; б) початкову глибину h, при якій рідина не буде виливатися з посудині, якщо W = 40 c-1, D2 = 0,5D1; в) максимальну кутову швидкість обертання Wmax , при якій рідина не буде виливатися з посудині та силу тиску на кришку у цьому випадку,якщо D2 = 0,7D1, h = 0,65 м; г) який об’єм рідини виллється з посудини і якою будe сила тиску на кришку, якщо D2 = 0,55D1, h = 0,66 м, W = 60 c-1. Вказівка. Попередньо слід встановити, де буде розташована вершина параболоїда обертання (вище або нижче дна посудини), і залежно від цього, скласти рівняння балансу об’ємів.
Задача 4.25. Закритий призматичний резервуар довжиною L = 2,2м,висотою H = 0,85 м і шириною b = 1,1 м заповнений рідиною=м3ρ 900 кг до глибини h з абсолютним тиском p0 на вільній поверхні (рис. 4.34). Резервуар рухається горизонтально з прискоренням j. Визначити сили тиску на бічні стінки А і В, якщо: а) h = 0,7 м, 2 сj = 2,2 м, 103 кПа p0 = ; б) h = 0,6 м, 2 сj =1,9 м, 99 кПа p0 = .
Задача 4.26. Циліндричний резервуар (рис. 4.35) діаметром D = 1м і з сегментною кришкою висотою b = nD заповнений вщерть рідиною з густиною ρ при показнику п’єзометра h і рухається по поверхні,що має кут нахилу α до горизонту з прискоренням j1, (або j2). Визначити сили, що відривають сегментну кришку, якщо: а) n = 0,5, м3ρ = 900 кг, h = 0,5 м, α = 70 о, 12 сj = 2 м, 2 2 сj = 4 м; б) n = 0,4, м3ρ = 1000 кг, h = 0,4м, α = 60 о, 12 сj = 4 м, 2 2 сj = 2 м; в) n = 0,3, м3ρ = 800 кг, h = 0,3 м, α = 50о, 12 сj = 5 м, 2 2 сj = 5 м.
Приклад 1. Для вимірювання глибини води у річці використовують дерев’яні жердини діаметром D = 5см та довжиною l = 5,5 м, густина деревини д 3 мρ = 650 кг . Визначити, яке зусилля треба прикласти до жердини, щоб виміряти глибину H = 4 м.
Приклад 2. Осадка h прямокутного понтона шириною b і довжиною l після завантаження піском з об’ємом Wп збільшилася на величину Dhп (рис. 5.3). Як зміниться осадка, якщо замість піску на понтон буде завантажено гравій об’ємом Wгр = 1,05Wп, густина якого на 10% менша, ніж густина піску?
Приклад 3. Брус прямокутного перерізу плаває у рідині з частковим зануренням (рис. 5.4). Визначити: а) відношення ширини b і висоти бруса H залежно від відношення густин матеріалу ρм і рідини ρр при остійному плаванні; б) при якому відношенні рмρρ забезпечується остійне плавання бруса квадратного перерізу.
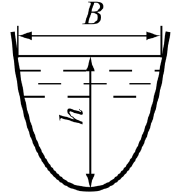
Задача 5.1. Визначити густину матеріалу циліндра круглого поперечного перерізу з діаметром D, що плаває у воді горизонтально і виступає з неї на висоту: а) 0,5 D; б) на 0,25D; в) 0,75D.
Задача 5.2. Закрита бочка (рис. 5.6) з довжиною H = 1,5 м і діаметром D = 70 см плаває у воді. Визначити об’єм бензину (б 3 мρ = 750 кг) у бочці, якщо маса порожньої бочки дорівнює m, її осадка з бензином h: а) m = 25 кг, h = 0,15 м; б) m = 15 кг, h = 0,10 м; в) m = 20 кг, h = 0,10 м.
Задача 5.3. Металева конструкція важить у повітрі G, а у воді G1. Визначити питому вагу металу, якщо: а) G = 1000 Н, G1 = 360 Н; б) G = 15000 кН, G1 = 1300 0 кН; в) G = 14000 кН, G1 = 12400 кН.
Задача 5.4. Циліндричний поплавок (рис. 5.7) з діаметром D = 110 мм і масою m плаває у резервуарі з водою і маслом (м 3 мρ = 780 кг), товщина шару останнього hм = 0,04 м. Визначити: а) осадку (глибину занурення) поплавка h, якщо m = 0,6кг; б) масу поплавка, якщо його глибина занурення h = 0,08 м; в) при якій максимальній густині матеріал у поплавка ρп він збереже плавучість, якщо його висота H = 90 мм?
Задача 5.5. На поверхню води у циліндричному резервуарі з площею W покладено тіло з масою m та густиною ρт, в наслідок чого рівень води підвищився на величину Dh. Визначити: а) масу тіла, якщо Dh =1,5 см, т 3 мρ = 800 кг,W = 10 м2; б) густину тіла, якщо Dh = 2,5 см, W = 8 м2, m = 510 кг; в) площу поверхні, якщо т 3 мρ = 250 кг, m = 210 кг, 91Dh = 3 см; г) підвищення рівня у резервуарі, якщо т 3 мρ = 600 кг,W = 15 м2, m = 310 кг.
Задача 5.6. Визначити мінімальну площу криги, яка б зберігала свою плавучість з однією людиною, маса якої 85 кг. Густина льоду л 3 мρ = 900 кг, густина води в 3 мρ = 1000 кг, товщина криги h: а) 0,5м; б) 0,25м.
Задача 5.7. Визначити об’єм пального з густиною п 3 мρ = 740 кг ,яким можна заповнити цистерну, що має зовнішню довжину l = 8 м, внутрішній діаметр D з товщиною стінок δ, та масу M, за умови збереження її плавучості, якщо: а) δ = 2 см, D = 1,3 м, M = 2300 кг; б) δ = 1,5 см, D = 1,15 м, M = 2100 кг.
Задача 5.8. Однорідна куля плаває у воді при зануренні на глибину h = nd (d– діаметр кулі). Визначити відношення густин матеріалу кулі та води, при:а) n = 0,6; б) n = 0,7; в) n = 0,8.
Задача 5.9. Визначити відносну глибину занурення dh однорідної кулі, густина якої менша, ніж густина води на: а) 30%; б) 20%; в) 60%.
Задача 5.10. Льодинка з розмірами 50 ´ 50 ´10 см вільно плаває у посудині, що заповнена водою, за температури С0o. Відносна густина льоду 0,9. Чи буде змінюватися рівень води у посудині,якщо лід буде танути? Поясніть чому.
Задача 5.11. Пліт складений з n колод, діаметром d = 0,25 м, довжиною l = 4 м, що розміщені у 2 ряди (рис. 5.8). Густина дерева д 3 мρ = 800 кг. Встановити: а) осадку плоту a при n = 28, якщо на плоту немає вантажу; б) теж саме при n = 20 і з вантажем масою M = 500 кг; в) вагу вантажу, при якому пліт буде повністю занурений у воду, якщо n = 24.
Задача 5.12. Жерстяна = ж 3 мρ 7800 кг куля подвійного поплавка,що заповнена повітрям (п 3 мρ =1,2 кг), використовується для вимірювання швидкості течії води та має плисти під водою (рис. 5.9). Визначити: a) радіус кулі при товщині жерсті δ = 1,5 мм; б) товщину жерсті δ, якщо радіус кулі r = 100 мм. Натяг гнучкого тросу не враховувати.
Задача 5.13. Тіло має масу m = 1кг, об’єм W = 1л. Яка сила потрібна для того, щоб його підняти: а) у воді; б) у повітрі; в) у нафті (н 3 мρ = 900 кг)?
Задача 5.14. Маса сталевого троса у повітрі становить m = 3 кг. Густина сталі ст 3 мρ = 7800 кг. Визначити вагу троса: а) у морській воді (в 3 мρ = 1020 кг); б) у бензині (б 3 мρ = 700 кг).
Задача 5.15. Для вимірювання поверхневих швидкостей руху використовують поплавки із деревини (рис. 5.10). Діаметр поплавка D = 25 см, густина дерева д 3 мρ = 650 кг. Визначити: а) висоту поплавка H, якщо його осадка h = 4 см; б) осадку поплавка h, якщо H = 7 см.
Вартість: 40 грн (Варіант а)
Задача 5.16. Визначити густину тіла, що у воді важить у n разів менше, ніж у повітрі, якщо: а) n = 1,5; б) n = 2; в) n = 2,5.
Задача 5.17. Людина може підняти у повітрі металеву кулю масою mі густиною ρ. Кулю із якою масою m1 і з того ж матеріалу вона може підняти у воді, якщо: а) m = 50 кг, 3 мρ = 7800 кг; б) m = 45 кг, 3 мρ = 4000 кг. Вказівка. У воді людина може підняти кулю іншого розміру.
Задача 5.18. Баржа із площею плавання W= 2500 м2 завантажується піском об’ємом W = 2000 м3. Визначити: а) густину піску ρп , якщо після його завантаження на баржу осадка збільшилася на Dh = 1,3м; б) зміну осадки баржі,якщо густина піску становить п 3 мρ = 1650 кг.
Задача 5.19. У призматичну посудину вагою G1, до якої налито рідину вагою G2, опускають тіло вагою G3 (рис. 5.11). Яка сила тиску буде діяти на підставку посудини під час рівномірного руху тіла у рідині?
Задача 5.20. У резервуарі, до якого налито дві рідини, що не змішуються, із густинами 1 3 мρ =1000 кг і 2 3 мρ =1200 кг, плаває куля з радіусом R, яка занурена на 0,5 R у нижню рідину (рис. 5.12). Визначити густину матеріалу кулі ρк, якщо вона виступає над поверхнею верхньої рідини на висоту: а) h = 0,5R; б) h = 0,25 R.
Задача 5.21. Об’єм крижаної гори (густина льоду л 3 мρ = 920 кг), що виступає над поверхнею океану, дорівнює 3W1 =15 м. Густина води в 3 мρ = 1030 кг. Знайти загальний об’єм гори та визначити глибину її занурення, якщо у плані вона має форму прямокутника із розмірами: а) a = 4 м, b = 5 м; б) a = 5 м, b = 8 м; в) a = 2 м, b = 3 м.
Задача 5.22. Перевірити умови остійності та обчислити глибину занурення однорідного конуса з радіусом основи r, кутом j, густиною ρ, що плаває у воді з оберненою догори вершиною (рис. 5.13), якщо: а) м3ρ = 750 кг, r = 1 м, j = 40о; б) м3ρ = 550 кг, r = 0,9 м, j = 50о; в) 3 мρ = 400 кг, r = 0,8 м, j = 75о.
Задача 5.23. У дні резервуара з водою є клапан з діаметром d2 = 1 см і масою M2, що приєднується гнучкою тягою до циліндричного поплавка з діаметром d1, глибиною занурення h1 і масою M1 (рис. 5.14). Визначити умови відкриття клапана,якщо відомі: а) M1 = 0,03 кг, h1 = 4 см, h2 = 100,5 cм, h3 = 0,5 см d1 = 7 см; б) M2 = 0,025 кг, h1 = 5 см, h2 = 0,81 м, h3 = 1 см, d1 = 6 см; в) M1 = 0,045 кг, M2 = 0,028 кг, h1 = 4,5см, h2 = 0,92 м, h3 = 2 см.
Задача 5.24. Плавучий залізобетонний зб 3 мρ = 2450 кг тунель із зовнішнім діаметром D і товщиною стінок δ при додатковому навантаженні f на 1 м довжини утримується у плавучому стані за допомогою тросів, які встановлені під кутом α через кожні 20 м по довжині тунелю (рис. 5.15). Визначити натяг тросів, якщо: а) D = 9,5 м, δ = 0,4 м, f = 10 кН, α = 55о; б) D = 10,5 м, δ = 0,45 м, f = 9 кН, α = 65о; в) D = 10 м, δ = 0,3 м, f = 8 кН, α = 60о.
Задача 5.25. Циліндр з матеріалу густиною ρм, діаметром D і висотою H плаває у воді вертикально із частковим зануренням. Визначити умови остійного плавання, тобто: а) відношення HD при м 3 мρ = 700 кг; б) відношення вмρρ при H > D ; в) відношення вмρρ при H < D.
Задача 5.26. Перевірити остійність дерев’яного прямокутного бруса з густиною ρд, шириною B, висотою H і довжиною L при плаванні у воді, якщо: а) д 3 мρ = 750кг, B = 30 см, Н = 20 см, L = 6м; б) д 3 мρ = 700 кг, B = 15 см, Н = 25 см, L = 5м; в) д 3 мρ = 720 кг, B = 20 см, H = 20 см, L = 4м.
Задача 5.27. Призматичне тіло з густиною ρт, шириною по верху b,висотою h і довжиною l > h у поперечному перерізі окреслено параболою (рис. 5.16). Тіло плаває постійно у рідині з густиною ρр. Визначити: а) значення ртρρ, якщо h = 1,5 b; б) значення hb, якщо 0,75 ρρрт = ; в) глибину занурення тіла у рідину при 0,65 ρρрт = і h = 0,7 м. Вказівка. Треба визначити глибину занурення для тіла, що окреслено параболою, потім центр ваги, ексцентриситет та умови остійного плавання залежно від hb.
Задача 5.28. Бруски квадратного поперечного перерізу з густиною ρбр плавають у рідині з густиною ρр (рис. 5.17). Встановити: а) яке положення брусків буде остійним при ρбр = 0,5 ρр; б) умови остійності при ρбр < 0,5ρр.
Задача 5.29. Обчислити глибину занурення h¢ та перевірити у мови остійності однорідного конуса з радіусом основи r, кутом j, густиною ρ, який плаває у воді з вершиною,що обернена донизу (рис. 5.18), якщо: а) м3ρ = 750 кг, r = 1 м, j = 40о; б) м 3ρ = 550 кг, r = 0,9 м, j = 50о; в) м 3ρ = 400 кг, r = 0,8 м, j = 75о.
Задача 5.30. У рідині з густиною ρр плаває півциліндра, густина матеріалу якого ρм = Nρр, радіусом r та довжиною l = 1,5 м (рис. 5.19). Визначити глибину h занурення його у рідину та метацентричну висоту пів циліндра hм, а також перевірити остійність плавання, якщо: а) N = 0,9, р 3 мρ = 800 кг, r = 1,0 м; б) N = 0,8, р 3 мρ = 900 кг, r = 0,9 м; в) N = 0,7, р 3 мρ = 1000 кг, r = 0,8 м.
Задача 5.31. Призма (густина її матеріалу ρм ) має у поперечному перерізі рівнобічний трикутник із сторонами a і плаває у воді горизонтально, як показано на схемі (рис. 5.20). Визначити: а) за яких умов плавання буде остійним; б) глибину занурення призми при м 3 мρ = 300 кг, а = 1 м.
Задача 5.32. Призма, що має у поперечному перерізі рівнобічний трикутник із сторонами a, плаває горизонтально, як показано на схемі (рис. 5.21). Визначити: а) за яких умов плавання буде остійним; б) глибину занурення, якщо густина матеріалу призми м 3 мρ = 650 кг, a = 0,9 м. Вказівка: При визначенні ексцентриситету необхідно враховувати центр ваги системи „бочка + нафта (бензин)”.
Задача 5.33. Кругла бочка з діаметром D = 0,5 м та висотою H = 1,2 м плаває у воді у вертикальному положенні.
Перевірити бочку на остійність, якщо: а) у бочці знаходиться 210 л нафти, густина якої н 3 м ρ = 900 кг, маса бочки 25 кг mб = ; б) у бочці перебуває 180 л бензину (б 3 м ρ = 750 кг), маса бочки mб = 20кг.
Вказівка: При визначенні ексцентриситету необхідно враховувати центр ваги системи „бочка + нафта (бензин)”.
Задача 5.34. Паром масою M = 4000 кг, шириною B = 4 м, довжиною l = 8м, висотою H = 0,9 м (рис. 5.22) призначений для перевезення автомобілів. Центр ваги парома розташований на половині його висоти, центр ваги автомобіля знаходиться на відстані CА h вище поверхні парома. Визначити осадку парома та його остійність, якщо: а) на ньому немає автомобіля; б) на паромі встановлений автомобіль вагою G = 55 кН, а1,1 мCА = h; в) на паромі встановлений автомобіль вагою G = 60 кН із вантажем масою Mв = 6000 кг при = 1,2 м А hC і центрі ваги вантажу на висоті = 1,5 м CB h від верхньої поверхні парома.
Часть задач есть решенные, контакты