Задачник по гидравлике гидромашинам и гидроприводу под.ред. Некрасова

Р.44

Задачник по гидравлике гидромашинам и гидроприводу под.ред.Б.Б.Некрасова

Решение задач по гидравлике

Есть готовые решения этих задач, контакты

Задача 1.3

Найти закон изменения давления p атмосферного воздуха по высоте z, считая зависимость его плотности от давления изотермической. В действительности до высоты z = 11 км температура воздуха падает по линейному закону, т. е. T = T₀ – βz, где β = 6,5 град/км. Определить зависимость p = f(z) с учетом действительного изменения температуры воздуха с высотой.

Задача 1.6

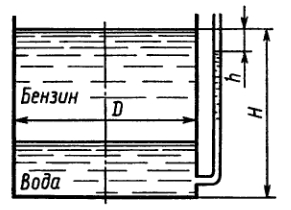
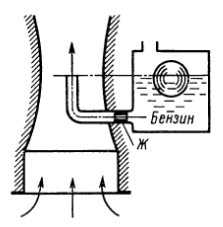
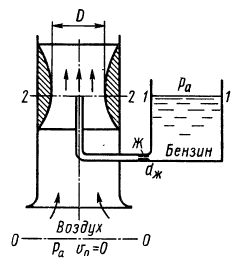
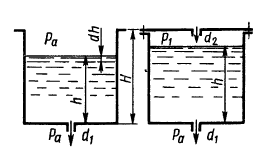
В цилиндрический бак диаметром D = 2 м до уровня H = 1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить вес находящегося в баке бензина, если ρ_б = 700 кг/м³.

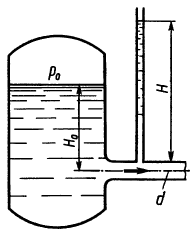
Задача 1.8

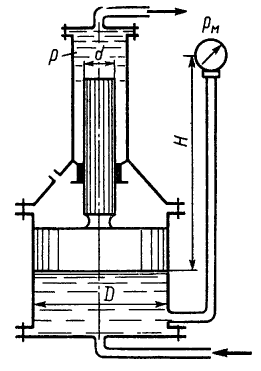
Определить избыточное давление p₀ воздуха в напорном баке по показанию манометра, составленного из двух U-образных трубок с ртутью. Соединительные трубки заполнены водой. Отметки уровней даны в метрах. Какой высоты H должен быть пьезометр для измерения того же давления p₀? Плотность ртути ρ_рт = 13600 кг/м³.

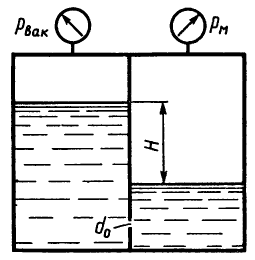
Задача 1.13

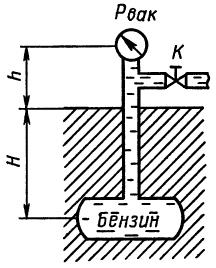
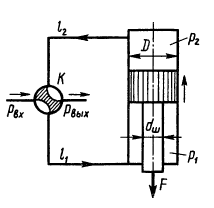
При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине H = 5 м, если показание вакуумметра, установленного на высоте h = 1,7 м, равно p_вак = 0,02 МПа. Атмосферное давление соответствует h_а = 740 мм рт. ст. Плотность бензина ρ_б = 700 кг/м³.

Задача 1.16

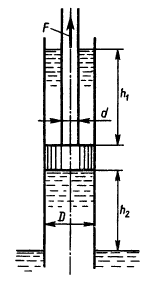
Определить давление в гидросистеме и вес груза G, лежащего на поршне 2, если для его подъема к поршню 1 приложена сила F = 1 кН. Диаметры поршней: D = 300 мм, d = 80 мм. Разностью высот пренебречь.

Задача 1.18

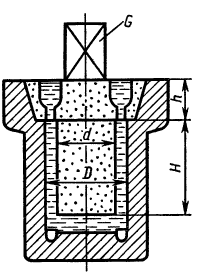
Определить минимальную силу тяжести груза G, который при заливке формы чугуном нужно положить на верхнюю опоку, чтобы предотвратить ее всплывание. Вес верхней опоки G_оп = 650 Н. Плотность жидкости чугуна ρ = 7000 кг/м³. Вес чугуна в литниках и выпорах не учитывать. Размеры: a = 150 мм; b = 150 мм; D₁ = 160 мм; D₂ = 300 мм.

Задача 1.19

Определить минимальную силу тяжести груза G, который при заливке формы чугуном нужно положить на верхний стержень, чтобы предотвратить его всплывание. Вес стержней с учетом веса чугуна в литнике и выпоре G₁ = 50 Н.

Плотность жидкого чугуна ρ = 7000 кг/м³; размеры: Н = 200 мм; D = 140 мм; h = 80 мм; d = 120 мм.

Задача 1.22

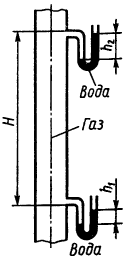
Избыточный напор газа на первом этаже дома составляет h₁ = 100 мм вод. ст. Определить избыточный напор h₂ газа на высоте H = 60 м, считая плотность воздуха и газа неизменными. Плотность газа ρ_г = 0,70 кг/м³, воздуха ρ_в = 1,29 кг/м³.

Задача 1.23

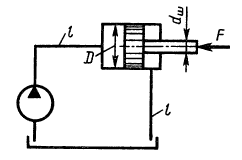
Определить силу F, необходимую для удержания поршня на высоте h₂ = 2 м над поверхностью воды в колодце. Над поршнем поднимается столб воды высотой h₁ = 3 м. Диаметры: поршня D = 100 мм, штока d = 30 мм. Вес поршня и штока не учитывать.

Задача 1.26

Определить давление p в верхнем цилиндре гидропреобразователя (мультипликатора), если показание манометра, присоединенного к нижнему цилиндру, равно p_м = 0,48 МПа. Поршни перемещаются вверх, причем сила трения составляет 10% от силы давления жидкости на нижний поршень. Вес поршней равен G = 4 кН. Диаметры поршней: D = 400 мм, d = 100 мм; высота H = 2,5 м; плотность масла ρ = 900 кг/м³.

Задача 1.31

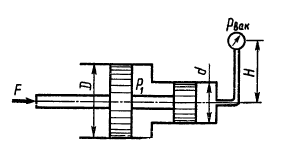
Определить силу F на штоке золотника, если показание вакуумметра р_вак = 60 кПа, избыточное давление р₁ = 1 МПа, высота Н = 3 м, диаметры поршней D = 20 мм и d = 15 мм, ρ = 1000 кг/м³.

Задача 1.34

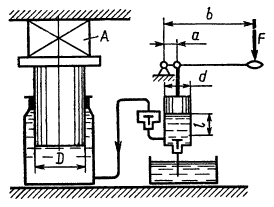
Давление в цилиндре гидравлического пресса повышается в результате нагнетания в него жидкости ручным поршневым насосом и сжатия ее в цилиндре. Определить число двойных ходов n поршня ручного насоса, необходимое для увеличения силы прессования детали А от 0 до 0,8 МН, если диаметры поршней: D = 500 мм, d = 10 мм; ход поршня ручного насоса l = 30 мм; объемный модуль упругости жидкости К = 1300 мПа; объем жидкости в прессе V = 60 л.

Чему равно максимальное усилие F на рукоятке насоса при ходе нагнетания, если b/а = 10?

Задача 1.35

Определить нагрузку на болты крышек A и Б гидравлического цилиндра диаметром D = 160 мм, если к плунжеру диаметром d = 120 мм приложена сила F = 20 кН.

Задача 1.40

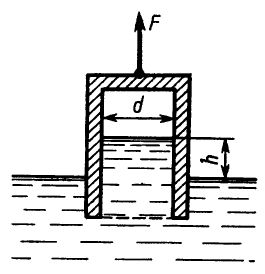
Определить абсолютное давление на поверхности жидкости в сосуде и высоту h, если атмосферное давление соответствует h_а = 740 мм рт. ст., поддерживающая сила F = 10 Н, вес сосуда G = 2 Н, а его диаметр d = 60 мм. Толщиной стенки сосуда пренебречь. Плотность жидкости ρ = 1000 кг/м³.

Купить задачу 1.40

Задача 1.45

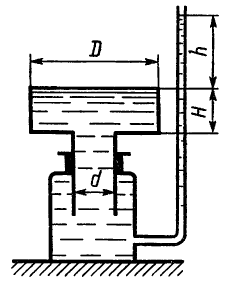
Определить высоту h столба воды в пьезометрической трубке. Столб воды уравновешивает полный поршень с D = 0,5 м и d = 0,2 м, имеющий высоту H = 0,3 м. Собственным весом поршня и трением в уплотнении пренебречь.

Купить задачу 1.45

Задача 1.46

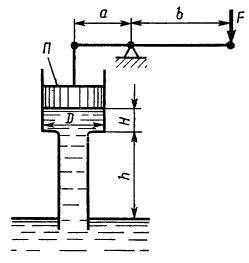
Определить силу F, необходимую для удержания в равновесии поршня П, если труба под поршнем заполнена водой, а размеры трубы: D = 100 мм, H = 0,5 м; h = 4 м. Длины рычага: а = 0,2 м и b = 1,0 м. Собственным весом поршня пренебречь.

Купить задачу 1.46

Задача 1.49

На рисунке представлена схема главного тормозного цилиндра автомобиля в момент торможения. Определить силу F, которую необходимо приложить к педали тормоза, чтобы давление в рабочих цилиндрах передних колес было р₁ = 6 МПа. Каким при этом будет давление в рабочих цилиндрах задних колес р₂? При расчете принять: усилие пружины 1 F₁ = 100 Н, пружины 2 F₂ = 150 Н, d = 20 мм, а = 60 мм, b = 180 мм. Силами трения пренебречь.

Задача 1.50

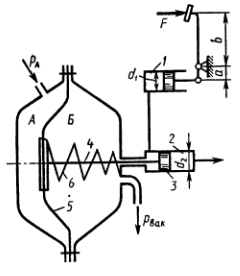
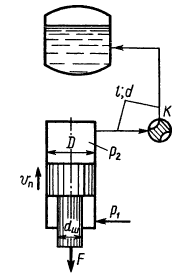
На рисунке показана принципиальная схема гидровакуумного усилителя гидропривода тормозов автомобиля. Давление жидкости, создаваемое в гидроцилиндрах 1 благодаря нажатию на ножную педаль с силой F, передается в левую полость тормозного гидроцилиндра 2. Помимо давления жидкости на поршень 3 в том же направлении действует сила вдоль штока 4, связанного с диафрагмой 5. Последняя отделяет полость А, сообщающуюся с атмосферой, от полости Б, где устанавливается вакуум благодаря соединению ее со всасывающим коллектором двигателя при нажатии на педаль. Пружина 6 при этом действует на диафрагму справа налево с силой F_пр. Определить давление жидкости, подаваемой из правой полости гидроцилиндра 2 к колесным тормозным цилиндрам. Принять: усилие педали F = 200 Н; сила пружины 6 F_пр = 20 Н; давление в полости Б p_вак = 0,06 МПа; диаметры: диафрагмы 5 D = 100 мм, гидроцилиндра 1 d₁ = 25 мм и гидроцилиндра 2 d₂ = 20 мм; отношение плеч b/a = 5. Площадью сечения штока 4 пренебречь.

Задача 2.2

Определить расход керосина, вытекающего из бака по трубопроводу диаметром d = 50 мм, если избыточное давление воздуха в баке равно p₀ = 16 кПа; высота уровня H₀ = 1 м; высота подъема керосина в пьезометре, открытом в атмосферу, равна H = 1,75 м. Потерями энергии пренебречь. Плотность керосина ρ = 800 кг/м³.

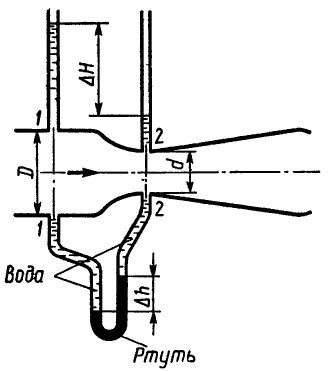
Задача 2.3

К расходомеру Вентури присоединены два пьезометра и дифференциальный ртутный манометр. Выразить расход воды Q через размеры расходомера D и d, разность показаний пьезометров ΔH, а также через показание дифференциального манометра Δh. Дан коэффициент сопротивления ζ участка между сечениями 1–1 и 2–2.

Задача 2.4

Определить весовой расход воздуха по трубе с плавно закругленным входом и цилиндрической частью диаметром D = 200 мм, если показание вакуумметра в виде вертикальной стеклянной трубки, опущенной в сосуд с водой, h = 250 мм. Коэффициент сопротивления входной части трубы (до места присоединения вакуумметра) ζ = 0,1. Плотность воздуха ρ_воз = 1,25 кг/м³.

Задача 2.6

Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте H = 2 м и постоянное избыточное давление p₂ = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d₁ = 75 мм, показывает p₁ = 0,25 МПа. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкости к баку, равен d₂ = 50 мм; коэффициент сопротивления этой трубы принять равным ζ = 0,5. Плотность жидкости ρ = 800 кг/м³.

Задача 2.9

Жидкость должна перетекать из резервуара А, где поддерживается постоянный уровень Н₁, в емкость Б. Для этой цели в дне резервуара устроено отверстие с закругленными входными кромками (ξ₀ = 0,05). Но расход жидкости через это отверстие оказался недостаточным. Каким способом и во сколько раз можно увеличить расход через отверстие, не меняя его диаметра и напора? Высота расположения выходного отверстия относительно нижнего уровня Н₂ = Н_1.

Указание. Следует установить диффузор (как показано пунктиром), который даст возможность использовать дополнительный напор Н₂ и превратить большую часть скоростного напора в давление (создать разрежение в горловине диффузора и, следовательно эффект подсоса).

Принять коэффициент сопротивления диффузора равным ξ_диф = 0,2 (отнесено к скорости в узком сечении), а степень расширения диффузора достаточно большой, чтобы можно было пренебречь скоростным напором на выходе из диффузора.

Задача 2.10

Для измерения расхода воды, которая подается по трубе А в бак Б, установлен расходомер Вентури В. Определить максимальный расход, который можно пропускать через данный расходомер при условии отсутствия в нем кавитации, если температура воды t = 60 °С (давление насыщенных паров соответствует h_н.п. = 2 м вод. ст.). Уровень воды в баке поддерживается постоянным, равным Н = 1,5 м; h = 0,5 м. Размеры расходомера: d₁ = 50 мм; d₂ = 20 мм. Атмосферное давление принять равным 760 мм рт. ст. Коэффициент сопротивления диффузора ζ_диф = 0,2.

Задача 2.11

Вода (ρ = 1000 кг/м³) перетекает из верхнего резервуара в нижний по расширяющейся трубе – диффузору, имеющему малый угол конусности и плавно закругленный вход. Пренебрегая потерей напора на входе в диффузор, определить, при какой уровне воды Н₁ в верхнем резервуаре абсолютное давление в узком сечении 1–1 диффузора сделается равным нулю. Коэффициент сопротивления диффузора ξ_диф = 0,2. Размеры: d₁ = 100 мм; d₂ = 150 мм; Н₂ = 1,15 м. Учесть потерю на внезапное расширение при выходе из диффузора. Атмосферное давление 750 мм рт. ст.

Указание. Учесть потерю кинетической энергии на выходе из диффузора по формуле Борда.

Задача 2.13

Определить расход воды, вытекающей из бака через короткую трубу (насадок) диаметром d = 30 мм и коэффициентом сопротивления ζ = 0,5, если показание ртутного манометра h_рт = 1,47 м, высоты H₁ = 1 м, H₀ = 1,9 м, l = 0,1 м.

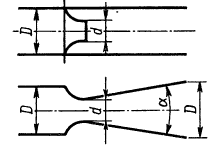
Задача 2.15

Сравнить коэффициенты сопротивления мерного сопла d, установленного в трубе D, и расходомера Вентури, состоящего из такого же сопла диаметром d и диффузора. Коэффициенты сопротивления определить как отношение суммарной потери к скоростному напору в трубопроводе. Дано отношение диаметров D/d = 2. Принять коэффициенты сопротивлений: сопла ζ_с = 0,05; диффузора ζ_диф = 0,15 (оба коэффициента относятся к скорости в узком сечении). Определить потери напора, вызываемые мерным соплом h_с и расходомером h_р, при одинаковой скорости потока в трубе υ = 3 м/с.

Указание. На выходе из сопла учесть потери напора на внезапное расширение.

Задача 2.16

Сравнить коэффициенты сопротивления расходомера Вентури, данные которого приведены в предыдущей задаче, и специального расходомера, показанного на рисунке. Последний состоит из диффузора (ζ_диф = 0,15), расширяющего поток до диаметра d₁ = 1,4d, внезапного расширения широкой части до диаметра D = 2,5d, в которой установлена решетка для выравнивания скоростей (ζ_р = 0,05) и сопла (ζ_с = 0,05). Коэффициенты отнесены к скорости в трубе диаметров d.

Задача 2.21

Определить минимальное давление p_м, измеряемое манометром перед сужением трубы, при котором будет происходить подсасывание воды из резервуара А в узком сечении трубы. Размеры: d₁ = 60 мм; d₂ = 20 мм; H₁ = 6 м; H₂ = 1 м. Принять коэффициенты сопротивления: сопла ζ_с = 0,08; диффузора ζ_диф = 0,30.

Задача 2.22

По длинной трубе диаметром d = 50 мм протекает жидкость (ν = 2 Ст; ρ = 900 кг/м³). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (Н = 80 см).

Задача 2.28

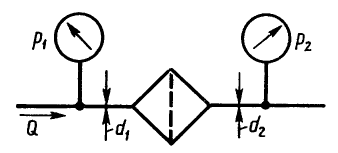
Для определения потерь давления на фильтре установлены манометры, как показано на рисунке. При пропускании через фильтр жидкости, расход которой равен Q = 1 л/с; давления: p₁ = 0,1 МПа, p₂ = 0,12 МПа. Определить, чему равна потеря давления в фильтре, если известно: d₁ = 10 мм, d₂ = 20 мм, ρ = 900 кг/м³.

Указание. Потерей давления на участках от мест установки манометров до фильтра пренебречь. Принять α₁ = α₂ = 1.

Задача 2.29

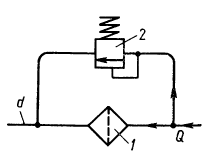
В гидросистеме с расходом масла Q = 0,628 л/с параллельно фильтру 1 установлен переливной клапан 2, открывающийся при перепаде давления на ∆р = 0,2 МПа. Определить вязкость ν, при которой начнется открытие клапана, если коэффициент сопротивления фильтра связан с числом Рейнольдса формулой ζ_ф = А/Re, где А = 2640; Re подсчитывается по диаметру трубы d = 20 мм; ρ = 850 кг/м³.

Задача 2.32

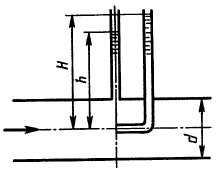
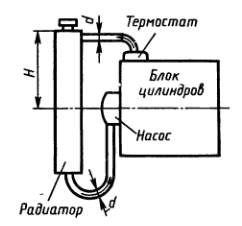
Определить напор, создаваемый насосом системы охлаждения автомобильного двигателя, при следующих данных: подача насоса Q = 3,9 л/с; коэффициенты сопротивления: блока цилиндров ζ₁ = 3,5; термостата ζ₂ = 2,5; радиатора ζ₃ = 4,0; трубы (шланга) от радиатора до насоса ζ₄ = 2,0. Все коэффициенты отнесены к скорости в трубе диаметром d = 40 мм. Чему равно абсолютное давление перед входом в насос, если в верхней части радиатора возник вакуум р_вак = 1 кПа; высота Н = 0,4 м; атмосферное давление соответствует h_а = 750 мм рт.ст., ρ_ж = 1000 кг/м³?

Задача 2.34

На рисунке показана схема двойного диффузора карбюратора, который обеспечивает больший вакуум, чем одинарный. Выходное сечение малого и узкое сечение большого диффузоров совпадают; в узком сечении малого диффузора расположен обрез распылителя бензина (наклонная трубка). Определить величину разрежения в сечении 1–1 при расходе воздуха G = 2 Н/с и следующих размерах: D = 40 мм; d₁ = 12 мм, d₂ = 20 мм. Принять следующие значения коэффициентов сопротивления участков воздушного потока: от 0–0 при p₀ = p_а и υ = 0 до 1–1 ζ₁ = 0,1; от 1–1 до 2–2 (внутри малого диффузора) ζ₂ = 0,2 (отнесены к площади πd₁²/4); от 0–0 до 2–2 (горловины большого диффузора) ζ₃ = 0,12 (отнесено к площади π(D² – d₂²)/4. Воздух считать несжимаемым, плотность ρ_воз = 1,25 кг/м³. Давление в горловине большого диффузора (2–2) считать равным давлению на выходе из малого диффузора.

У к а з а н и е. Следует записать уравнение суммы расходов через диффузоры G₁ и G₂ и уравнения Бернулли для воздушных потоков от 0–0 до 2–2 внутри малого диффузора и вне его. Система трех уравнений с тремя неизвестными G₁, G₂ и p_а – p₂ позволяет найти расход через малый диффузор G₁. Затем из уравнения Бернулли для сечений 1–1 и 2–2 (внутри малого диффузора) определяется искомое разрежение (вакуум) p_а – p₁. Расходом бензина пренебречь.

Задача 3.3

Определить направление истечение жидкости (ρ = ρ_вод) через отверстие d₀ = 5 мм и расход, если разность уровней Н = 2 м, показание вакуумметра p_вак соответствует 147 мм рт. ст., показание манометра p_м = 0,25 МПа, коэффициент расхода μ = 0,62.

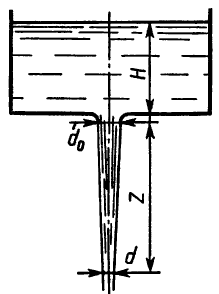
Задача 3.6

Жидкость вытекает через сопло диаметром d₀, устроенное в горизонтальном дне сосуда. Найти связь между диаметром струи d и высотой z, если напор равен Н. Сопротивлениями пренебречь.

Задача 3.12

Как изменится расход воды Q (%) через внешний цилиндрический насадок (μ = 0,82) диаметром d₀ = 20 мм, если к нему привинтить цилиндрическую трубку диаметром d = 30 мм и получить истечение с заполнением выходного сечения трубки? Потерей на трение по длине пренебречь. Подсчитать максимальный расход, при котором возможно такое истечение. Принять коэффициент сжатия струи насадка ε = 0,64; h_A = 750 мм рт. ст.; h_н.п = 40 мм рт. ст.

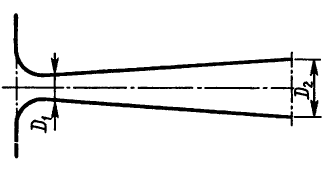
Задача 3.16

Дан диффузорный насадок с плавно закругленным входом в виде сопла (ζ_с = 0,06) и диффузора с оптимальным углом конусности (α = 5°30´) и с соотношением диаметров D₂/D₁ = 3, для которого можно принять коэффициент сопротивления ζ = 0,125. Коэффициенты сопротивления отнесены к узкому сечению. Определить для данного насадка коэффициент расхода μ, отнесенный к площади выходного отверстия (D₂), и коэффициент расхода μ’, отнесенный к площади узкого сечения (D₁).

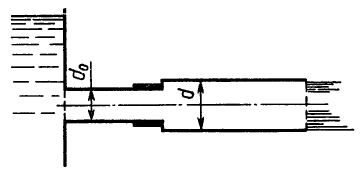
Задача 3.17

Для выпуска воды из бака в его стенке устроено отверстие и введена труба, как показано на рисунке. Однако пропускная способность полученного насадка (внутреннего цилиндрического) оказалась недостаточной. Во сколько раз можно увеличить пропускную способность указанной трубы, не меня ее диаметра и напора, если приставить к ней сопло (внутри бака) и диффузор снаружи? Трением внутри трубки пренебречь. Значения коэффициентов сопротивления сопла и диффузора, а также степень расширения диффузора взять из предыдущей задачи. Режим истечения в обоих случаях считать безотрывным и безкавитационным.

Задача 3.19

При испытании модели гидротурбинного сопла диаметром d₀ = 65 мм были произведены следующие измерения: давление воды в широкой части сопла (диаметром D = 160 мм) p₁ = 0,9 МПа; расход Q = 96 л/с; диаметр струи d_с = 55 мм. При помощи динамометра измерена сила воздействия струи на преграду F = 3,88 кН (диск установлен нормально к струе). Определить коэффициенты расхода μ и  сопротивления ζ двумя различными способами.

Задача 3.20

На рисунке показана упрощенная схема самолетного гидропневмоамортизатора. Процесс амортизации при посадке самолета происходит за счет проталкивания рабочей жидкости через отверстие d = 8 мм и за счет сжатия воздуха. Диаметр поршня D = 100 мм. Определить скорость движения цилиндра относительно поршня в начальный момент амортизации, если первоначальное движение воздуха в верхней части амортизатора p₁ = 0,2 МПа, расчетное усилие вдоль штока G = 50 кН, коэффициент расхода отверстия μ = 0,75, плотность рабочей жидкости ρ = 900 кг/м³.

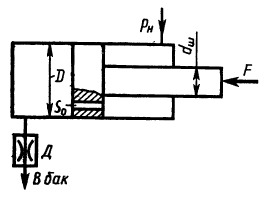
Задача 3.27

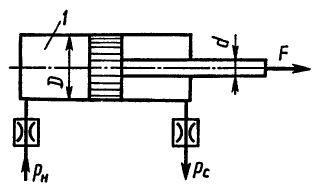
Жидкость с плотностью ρ = 850 кг/м³ подается от насоса в гидроцилиндр, а затем через отверстие в поршне площадью S₀ = 5 мм² и гидродроссель Д в бак (р₆ = 0).

1) Определить, при какой площади проходного сечения дросселя Д поршень будет находиться в неподвижном равновесии под действием силы F = 3000 Н, если диаметр поршня D = 100 мм, диаметр штока d_ш = 80 мм, коэффициент расхода отверстия в поршне μ₀ = 0,8, коэффициент расхода дросселя μ_др = 0,65, давление насоса р_н = 1 МПа. 2) Определить площадь проходного сечения дросселя Д, при которой поршень будет перемещаться со скоростью υ_п = 1 см/с вправо.

Задача 3.28

Правая и левая полости цилиндра гидротормоза, имеющего диаметр поршня D = 140 мм и диаметр штока d_ш = 60 мм, сообщаются между собой через дроссель с площадью проходного сечения S_др = 20 мм² и коэффициентом расхода μ = 0,65. Определить время, за которое поршень переместится на величину хода l = 350 мм под действием силы F = 15 кН, плотность жидкости ρ = 900 кг/м³.

Задача 3.31

Редукционный клапана предназначен для обеспечения постоянного давления на выходе из него р₂ = 11 МПа. Определить требуемые жесткость пружины и ее предварительное поджатие (при полностью открытом клапане), обеспечивающие изменение давления за клапаном Δр₂ = ± 4%р₂, если его диаметр d = 12 мм, максимальный ход t = 3 мм, угол конуса α = 60°, коэффициент расхода дросселирующей щели А μ = 0,8, плотность рабочей жидкости ρ = 900 кг/м³. Каков максимальный расход жидкости через клапан, если максимальное давление перед ним р₁ = 12 МПа?

У к а з а н и е. Площадь проходного сечения конусной щели А определить по упрощенной формуле S_щ = πdh sin (α/2), где h – ход клапана.

Задача 3.32

Считая жидкость несжимаемой, определить скорость движения поршня под действием силы F = 10 кН на штоке, диаметр поршня D = 80 мм, диаметр штока d = 30 мм, проходное сечение дросселя S_др = 2 мм², его коэффициент расхода μ = 0,75, избыточное давление слива p_с = 0, плотность рабочей жидкости ρ = 900 кг/м³.

Задача 3.36

Определить расход бензина через жиклер Ж карбюратора диаметром d = 1,2 мм, если коэффициент расхода жиклера μ = 0,8. Сопротивлением бензотрубки пренебречь. Давление в поплавковой камере атмосферное. Дано разрежение (вакуум) в горловине диффузора р_вак = 18 кПа, ρ_б = 750 кг/м³.

Задача 3.37

На рисунке показан простейший карбюратор двигателя внутреннего сгорания. Поток воздуха, засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки). Скорость воздуха в этом сечении возрастает, а давление падает. Благодаря этому бензин подсасывается из поплавковой камеры и вытекает через распылитель, смешиваясь с потоком воздуха. Найти соотношение между массовыми расходами воздуха и бензина Q_воз/Q_б, если известны: размеры D = 30 мм; d_ж = 1,8 мм; коэффициент сопротивления воздушного канала до сечения 2–2 ζ_в = 0,05; коэффициент расхода жиклера μ = 0,8. Сопротивлением бензотрубки пренебречь. Плотности: воздуха ρ_воз = 1,25 кг/м³; бензина ρ_б = 750 кг/м³.

Указание. Следует записать уравнение Бернулли для воздушного потока (сечение 0–0 и 2–2) и уравнение истечения для бензина. При этом учесть, что давление бензина и воздуха в сечении 2–2 одинаковы.

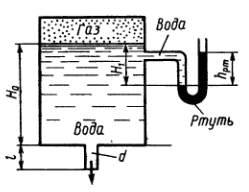
Задача 3.43

Определить время полного опорожнения цилиндрического бака, заполненного жидкостью. Площадь основания бака S = 1 м² и высота Н = 1 м.

Истечение происходит в атмосферу через отверстие в дне бака с закругленными кромками (сопло) диаметром d₁ = 10 мм. Задачу решить, если:

1) бак открыт и давление воздуха на поверхности жидкости атмосферное;

2) бак закрыт, но в крышке имеется отверстие диаметром d₂ = 3 мм. Воздух при опорожнении бака всасывается через это отверстие и над поверхностью жидкости создается разрежение.

Коэффициент расхода отверстий принять μ = 1.

Воздух считать не сжимаемым, плотность ρ_возд = 1,3 кг/м³.

Задача 4.4

Определить режим течения жидкости при температуре 10 °С (ν = 0,4 Ст) по трубопроводу длиной l = 3 м, который при перепаде давления Δp = 2 МПа должен обеспечивать расход Q = 1 л/с. Плотность ρ = 850 кг/м³.

Указание. Воспользоваться выражением для числа Re через Q и законом Пуазейля, исключить из них диаметр d и, определив перепад давления, соответствующий смене режима, сравнить его с заданным перепадом.

Задача 4.8

Жидкость с плотностью ρ = 900 кг/м³ и вязкостью ν = 0,01 Ст нагнетается по горизонтальному трубопроводу длиной l = 4 м и диаметром d = 25 мм. Определить давление в начальном сечении, если в конечном сечении трубопровода давление атмосферное, расход жидкости Q = 6 л/с; шероховатость стенок трубопровода Δ = 0,06 мм.

Задача 4.16

Труба, соединяющая два бака, заполнена жидкостью с вязкостью ν = 0,01 Ст и плотностью 1000 кг/м³. Определить при какой высоте H жидкость будет двигаться из верхнего бака в нижний с расходом Q = 0,05 л/с, а при какой высоте H будет двигаться в обратном направлении с тем же расходом, если длина трубы l = 2,5 м; ее диаметр d = 8 мм; коэффициент сопротивления каждого колена ζ = 0,5; избыточное давление в нижнем баке p₀ = 7 кПа; вакуум в верхнем баке p_вак = 3 кПа. Трубу считать гидравлически гладкой.

Задача 4.28

На трубопроводе диаметром D = 400 мм, подводящем воду к ТЭЦ, установлен трубчатый подогреватель воды. Сумма живых сечений трубок (d = 25 мм) сделана примерно равной площади сечения трубопровода; длина трубок l = 0,5L; число трубок n = 256. Пренебрегая сопротивлением конусов и потерями на входе в трубки и на выходе из них, определить, во сколько раз сопротивление подогревателя больше сопротивления участка трубопровода диаметром D и диной L, на место которого установлен подогреватель. Использовать формулу Блазиуса.

Задача 4.30

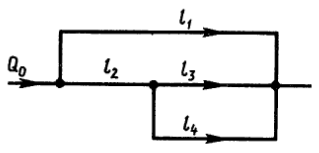
На рисунке показан сложный трубопровод. Определить расходы в каждом из простых трубопроводов, если их длины соответственно равны: l₁ = 5 м, l₂ = 3 м, l₃ = 3 м, l₄ = 6 м, а суммарный расход Q = 6 л/мин. Считать, что режим течения ламинарный, а диаметры трубопроводов одинаковы.

Задача 4.33

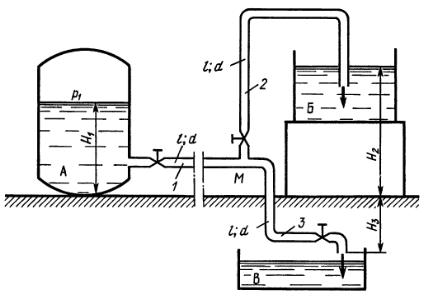
Вода подается из бака А в количестве Q₁ = 3,2 л/с по трубе 1 длиной l = 6 м и диаметром d = 30 мм к разветвлению М, от которого по двум одинаковым трубам 2 и 3 длиной l и диаметром d подается в резервуары Б и В. Приняв коэффициент сопротивления трения одинаковым и равным λ_т = 0,03, а также коэффициенты сопротивлений всех трех кранов одинаковыми и равными ζ_к = 3,5, определить расходы воды Q₂ и Q₃, подаваемой в бак Б и резервуар В, а также давление в баке А. Сопротивлением колен и тройника пренебречь. Высоты: Н₁ = 7,4 м; Н₂ = 4 м; Н₃ = 0,6 м.

Задача 4.35

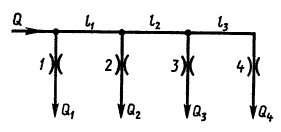
По трубопроводу длиной l = l₁ + l₂ + l₃ движется жидкость, истекающая по пути следования через дроссели 1…4 в атмосферу. Движения жидкости в трубопроводе на всех участках происходит в области квадратичного сопротивления. Коэффициенты сопротивлений всех дросселей одинаковы и равны ζ. Найти соотношение между участками трубопровода l₁; l₂; l₃, если Q₃ = 2Q₄; Q₂ = 2Q₃; Q₁ = 2Q₂, а диаметры всех труб d.

Задача 5.8

Показать, что зависимость механического к.п.д. от подачи η_м = f(Q) для центробежного насоса монотонно приближается к пределу при угле между относительной и окружной скоростями β₂ ≥ 90° и имеет экстремум при β₂ < 90°. Считать мощность механических потерь не зависящей от подачи.

Задача 5.9

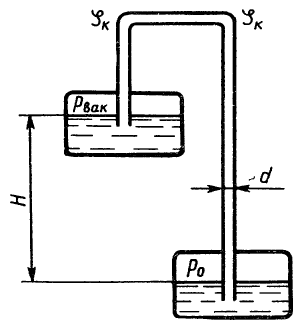
Компенсационный бачок системы охлаждения двигателя внутреннего сгорания расположен на 0,5 м выше оси вращения вала насоса и соединен с атмосферой. Определить кавитационный запас и разность между ним и критическим кавитационным запасом при температуре воды t = 80°С (р_н.п. = 45 кПа), если кавитационный коэффициент быстроходности, по формуле Руднева, С = 1200; Q = 5 л/с; n = 6000 об/мин; h_а = 740 мм рт. ст. Диаметр входного трубопровода d = 40 мм.

 Задача 5.10

Определить разность между кавитационным запасом и критическим кавитационным запасом для центробежного насоса предыдущей задачи при движении по шоссе (высота над уровнем моря Н = 4200 м, атмосферное давление h_а = 740 мм рт. ст.).

Задача 5.17

Центробежный насос системы охлаждения двигателя внутреннего сгорания работал с подачей Q = 8 · 10^-3 м³/с и с частотой вращения n = 250 с^-1. После модернизации системы охлаждения двигателя диаметр рабочего колеса увеличили в 1,3 раза. Определить напор нового насоса, если его подача и частота вращения остались неизменными. Принять, что характеристика исходного насоса описывается тем же уравнением, что и в задаче 5.16.

Задача 5.26

Двухкамерный гидродвигатель поворотного движения должен создавать момент на валу, равный M = 2 кН · м при скорости поворота ω = 2 с^-1. Размеры гидродвигателя: D = 200 мм; d = 100 мм (см. рис.); ширина лопастей b = 60 мм. Принять механический к.п.д. η_м = 0,9; объемный к.п.д. η₀ = 0,75. Определить потребное давление насоса и необходимую подачу.

 

Задача 6.4

Определить давление, создаваемое насосом, и его подачу, если преодолеваемая сила вдоль штока F = 10 кН, а скорость перемещения поршня υ_п = 0,1 м/с. Учесть потерю давления на трение в трубопроводе, общая длина которого l = 8 м; диаметр d = 14 мм. Каждый канал распределителя по сопротивлению эквивалентен длине трубопровода l_э = 100d. Диаметр поршня D = 100 мм, площадью штока пренебречь. Вязкость масла ν = 1 Ст; плотность ρ = 900 кг/м³.

Задача 6.6

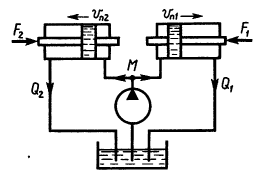
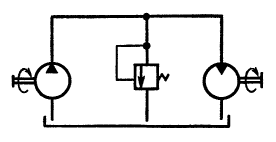
Определить скорости поршней υ_п1 и υ_п2, площади которых одинаковы и равны S_п = 5 см². Штоки поршней нагружены силами F₁ = 1 кН и F₂ = 0,9 кН. Длина каждой ветви трубопровода от точки М до бака l = 5 м; диаметр трубопроводов d = 10 мм; подача насоса Q = 0,2 л/с. Вязкость рабочей жидкости ν = 1 Ст; плотность жидкости ρ = 900 кг/м³.

Задача 6.8

Определить перепад давления в силовом гидроцилиндре ∆р_ц, шток которого нагружен постоянной силой F = 16 кН, в следующих двух случаях: 1) скорость подъема поршня равна υ_п = 0; 2) υ_п = 0,2 м/с. Диаметры: поршня D = 60 мм; штока d_ш = 20 мм. Трубопровод, по которому жидкость движется из гидроцилиндра через распределитель К в бачок, имеет длину l = 6 м; диаметр d = 10 мм. Свойства жидкости: ν = 4 Ст; ρ = 850 кг/м. Сопротивлением распределителя К пренебречь. Избыточное давление в баке считать равным нулю, нивелирные высоты не учитывать.

У к а з а н и е. Следует записать уравнение равновесия поршня и из него выразить ∆р_ц через давление р₂, которое является функцией скорости в трубопроводе.

Задача 6.9

Определить перепад давления на входе и выходе распределителя Δp_р, к которому присоединена магистраль с силовым гидроцилиндром. Диаметры: поршня D = 60 мм; штока d_ш = 30 мм; расход жидкости на входе в распределитель Q = 0,314 л/с. Шток гидроцилиндра нагружен силой F = 16 кН. Длина подводящего участка магистрали l₁ равна длине отводящего участка и составляет l₁ = l₂ = 8 м; диаметр трубопровода d = 10 мм; свойства рабочей жидкости: ρ = 850 кг/м³, ν = l Ст.

У к а з а н и е. 1. Перепад давления в гидроцилиндре Δp_ц определить как частное от деления силы F на площадь поршня S_п со стороны нагнетания. 2. Учесть, что скорости в подводящем участке магистрали υ₁ и отводящем участке υ₂ будут различными.

Задача 6.10

Определить давление, создаваемое насосом, если длины трубопроводов до и после гидроцилиндра равны l = 5 м; их диаметры d_т = 15 мм; диаметры: поршня D = 60 мм; штока d_ш = 40 мм; сила на штоке F = 1 кН; подача насоса Q = 1,2 л/с; вязкость рабочей жидкости ν = 0,5 Ст; плотность ρ = 900 кг/м³.

Задача 6.13

Найти минимальные рабочие объемы гидромашин гидропередачи, обеспечивающие на выходном валу гидромотора момент M = 50 Н × м и угловую скорость ω₂ = 200 с^-1, если угловая скорость насоса ω₁ = 300 c^-1, давление срабатывания предохранительного клапана p_кл = 15 МПа. Принять объемные к.п.д. гидромашин η₀ = 0,95; механические к.п.д. – η_м = 0,92. Какую мощность при этом потребляет насос?

Задача 6.16

Определить минимально допустимый диаметр дроссельной шайбы в напорной линии гидропривода d₁, обеспечивающей перемещение поршня гидроцилиндра без разрыва сплошности потока (без кавитации) в полости 1. Перемещение поршня происходит под действием лишь нагрузки на штоке F = 20 кН. Давления: насоса р_н = 15 МПа; слива р_с = 0,5 МПа; насыщенных паров жидкости р_н.п = 0,01 МПа. Диаметры: цилиндра D = 50 мм; штока d = 30 мм; дроссельной шайбы на сливе d₂ = 1,5 мм. Коэффициент расхода дроссельных шайб μ = 0,64. Плотность жидкости ρ = 900 кг/м³.

Задача 6.17

В системе гидропривода постоянного давления нагнетания р_н = 25 МПа и слива р_с = 1 МПа установлен гидроцилиндр с дроссельным регулированием скорости поршня с помощью одинаковых дросселей на нагнетании и сливе, открывающихся синхронно. Определить минимальный диаметр гидроцилиндра, площади открытия дросселей и скорость поршня без нагрузки при условии, что шток поршня должен преодолевать нагрузку F = 35 кН при скорости перемещения υ = 150 мм/с. Плотность жидкости ρ = 850 кг/м³; диаметр штока d = 40 мм; коэффициент расхода дросселей μ = 0,64.

Задача 6.37

Гидравлическая объемная трансмиссия активного автоприцепа включает в себя регулируемый насос 1, который через фильтр 2подает рабочую жидкость к двум гидромоторам 3. Свойства жидкости: ν = 0,2 Ст; ρ = 900 кг/м³. Выходные валы гидромоторов связаны с ведущими колесами 5 через редукторы 4 с передаточными отношениями i = n_г м/n_к.

Определить число оборотов колес и мощности, потребляемую насосом, при условии, что моменты нагрузки на левом М_л и правом М_пр колесах различны. Задачу решить при следующих данных: М_л = 2,9 кН · м; М_пр = 3,1 кН · м; i = 15; l₁ = l₂ = 12 м; l₂ = l₃ = 3 м; l_ф = 200 d₁; d₁ = d₄ = 24 мм; d₂ = d₃ = 10 мм; частота вращения насоса n₁ = 2000 об/мин; рабочие объемы гидромашин М = 150 см³. Коєффициенті полезного действия гидромашин принять : η₀ = 0,95 (при р = 10 МПа); η_м = 0,95; η = 0,9. Механическими потерями в редукторе пренебречь.

Указание. Задача решается графоаналитическим методом.

 

Есть готовые решения этих задач, контакты