ВК блог

ТТ.127

Часть задач есть решенные, контакты

1. Термодинамические параметры

1.1. Слиток свинца, имеющего плотность ρ = 11,3 г/см³, объемом V = 1 дм³ взвешен при помощи пружинных весов на полюсе, где ускорение свободного падения g₉₀º = 9,8324 м/с². Каков вес свинца, выраженный в ньютонах и в килограмм-силах? Что покажут пружинные весы на экваторе, где g₀º = 9,780 м/с²?

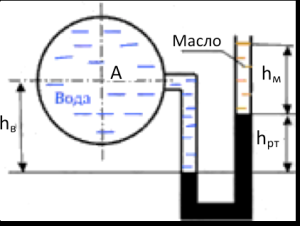
1.2. Манометр, установленный в открытой кабине самолета, находящегося на земле, и измеряющий давление масла, показывает 6 кгс/см² при показаниях барометра 752 мм рт.ст.

1. Каково абсолютное давление масла, выраженное в ньютонах на квадратный метр, килограмм илах на квадратный сантиметр, мегапаскалях, миллиметрах ртутного столба, миллиметрах водяного столба?
2. Каковы будут показания манометра в этих же единицах после подъема самолета на некоторую высоту, где атмосферное давление В = 442,5 мм рт.ст., если абсолютное давление остается неизменным?

Ускорение свободного падения [g_м = 0,98055 м/с²] считать нормальным и не зависящим от высоты подъема самолета. Плотность ртути и воды принимать соответственно при 0º и 4ºС:

ρ_Нg0º_С = 13,596 · 10³ кг/м³;               ρ_Нg4º_С = 1,0 · 10³ кг/м³.

1.3. В конденсаторе паровой турбины поддерживается абсолютное давление р = 0,004 МПа. Каковы показания вакуумметров, проградуированных в килоньютонах на квадратный метр, миллиметрах ртутного столба и в английских фунтах на квадратный дюйм, если в одном случае показания барометра составляют 735 мм рт.ст., а в другом – 764 мм рт.ст.?

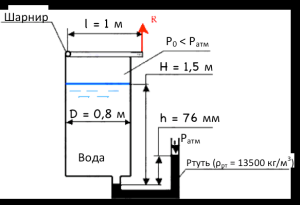
1.4. Цилиндр диаметром d = 200 мм [рис. П.1.1]* плотно закрыт подвешенным на пружине поршнем, условно невесомым и скользящим без трения. В цилиндре образован вакуум, составляющий ω = 90% барометрического давления В = 0,101 МПа. Определить силу F натяжения пружины, если поршень неподвижен.

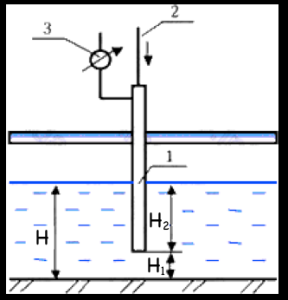
1.5. Для измерения малых избыточных давлений или небольших разряжений применяются микроманометры. Принципиальная схема прибора представлена на рис. П.1.2. Определить абсолютное давление в воздухопроводе 1, если длина столба l жидкости в трубке микроманометра 2, наклоненной под углом α = 30º, равна 180 мм. Рабочая жидкость – спирт плотностью ρ = 0,8 г/см³. Показание барометра 0,1020 МПа. Давление выразить в мегапаскалях, миллиметрах ртутного столба и в килограмм-силах на квадратный сантиметр.

1.3. В паросборнике находится водяной пар в количестве 300 кг. Определить объем паросборника, если удельный объем пара ν = 20,2 г/см³.

1.7. Объем баллона, содержащего газ под давлением р = 1,2 · 10⁵ Па, составляет V = 6 л. Каким станет давление ρ₂ газа в баллоне, если его соединить с другим баллоном объемом V* = 10 л, практически не содержащим газа [температура остается постоянной]?

1.8. В баллон емкостью V = 12 л поместили m₁ = 1,5 кг азота при температуре t₂ = 327ºС. Какое давление ρ₂ будет создавать азот в баллоне при температуре t₂ = 50ºС, если 35% азота будет выпущено? Каково будет начальное давление р1?

1.9. На дне сосуда, заполненного воздухом, лежит полный стальной шарик радиусом r = 2 см. Масса шарика m_м = 5 г. До какого давления р надо сжать воздух в сосуде, чтобы шарик поднялся вверх? Считать, что воздух при больших давлениях подчиняется уравнению газового состояния. Температура воздуха t = 20ºС = const (сжатия воздуха происходит достаточно медленно).

1.10. При нагревании газа на 1 К при постоянном давлении его объем увеличился на 0,005 первоначального.  При какой температуре находился газ?

1.11. Два баллона соединены трубкой с краном. В первом баллоне газ находится под давлением р₁ = 2 · 10⁵ Па, во втором – под давлением р₂ = 1,2 · 10⁵ Па. Емкость первого баллона V = 2 л, второго V = 6 л. Температура газов в обоих баллонах одинакова. Какое давление установится в баллонах, если открыть кран?

1.12. На какой глубине радиус пузырька воздуха вдвое меньше, чем у поверхности воды, если барометрическое давление у поверхности равно р₂?

1.13. Цилиндр с газом разделен на четыре камеры тремя навесными поршнями (рис. П.1.3). В каждой секции находится газ, состояние которого характеризуется параметрами р₁V₁Т₁, р₂V₂Т₂, р₃V₃Т₃. Каковы будут объемы и давления в каждой секции после того, как освободить поршни и дать им возможность свободно двигаться, а температуру изменить до Т₂?

1.14. В U-образной трубке, запаянной с одного конца, высота столба воздуха l = 300 мм, а высота столба ртути h₀ = 110 мм (рис. П.1.4). В правое колено долили столько ртути, что ее уровень поднялся на Δh₀ = 40 мм. Насколько поднялся уровень ртути в левом колене? Атмосферное давление р₀ = 1,01 · 10⁵ Па (760 мм рт.ст.).

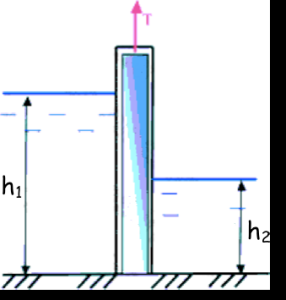
1.15. После погружения металлической трубки в резервуар с водой оказалось, что уровень воды в трубке поднялся на высоту 0,75 м при длине трубки 0,95 м. Определить глубину погружения трубки в резервуар Н, если барометрическое давление В = 750 мм рт.ст.

2. Законы идеальных газов. Уравнение состояния

2.1. Начальное состояние азота задано параметрами t = 200ºС, ν = 1,9 м³/кг. Азот нагревается при постоянном давлении, причем объем азота увеличивается до 5,7 м³/кг. Определить конечную температуру.

2.2. В цилиндре с подвижным поршнем находится кислород при t = 80ºС и разрежение (вакуум), равном 427 гПа. При постоянной температуре кислород сжимается до избыточного давления р_изб = 1,2 МПа. Барометрическое давление В = 993 гПа. Во сколько раз уменьшится объем кислорода?

Стоимость: 60 руб

2.3. Баллон емкостью V, наполненный газом при давлении р и температуре Т взвесили, причем его вес оказался равным Р. Из баллона откачали часть газа, после чего давление упало до р₁ при той же температуре. Вес баллона в этом случае оказался равным Р₁. Определить плотность газа при нормальных условиях.

2.4. В комнате объемом V₁ = 60 м³ температура поднялась с t₁ = 17º до t₂ = 27ºС. Давление при этом изменилось от р₁ = 1,03 · 10⁵ Па до р₂ = 1,03 · 10⁵ Па (среднюю массу одного киломоля воздуха принять равной μ = 29 кг/кмоль) На какую величину Δm изменилась  масса воздуха в комнате?

2.5. Плотность пара некоторого соединения углерода с водородом равна ρ = 3 кг/м³ при температуре 43ºС и давлении 99 · 10³ Па. Какова молекулярная масса этого соединения?

2.6. Определить температуру газа, находящегося в закрытом баллоне, если его давление, увеличилось на 0,4% первоначального при нагревании на ΔТ = 1 К.

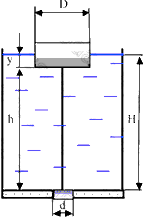
2.7. Сколько ртути войдет в стеклянный баллончик объемом V₀, нагретый до температуры t₀, при его остывании до t₁, если плотность ртути при t₁ равна ρ (рис. П.1.5)?

2.8. Тонкостенный резиновый шар собственным весом Р = 0,6 Н наполнен неоном и погружен в озеро на глубину h = 120 м. Найти массу неона, если шар находится в положении равновесия. Атмосферное давление р₀ = 1,03 · 10⁵ Па температура в глубине озера t = + 4ºC. Натяжением резины пренебречь.

2.9. По газопроводной трубе идет углекислый газ при давлении р = 4,9 · 10⁵ Па и температуре t = 21ºС. Какова скорость ν движения газа в трубе, если за время τ = 10 мин протекает m = 3 кг углекислого газа, а площадь сечения трубы S = 5 см²?

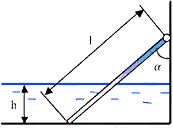
2.10. Стеклянная запаянная с одного конца трубка длиной l = 20 см, содержащая некоторое количество воздуха, погружена в ртуть так, что над поверхностью выступает l₁ = 15 см трубки. Уровень ртути в трубке при 0ºС выше уровня ртути в сосуде на h₁ = 5 см. На сколько градусов нужно было нагреть воздух в трубке, чтобы он мог занять весь объем трубки? Атмосферное давление р = 105 Па, уровень ртути в сосуде считать неизменным (рис. П.1.6).

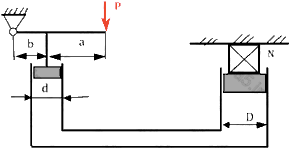
2.11. Вертикально расположенный цилиндрический сосуд разделен на две равные части тяжелым теплонепроницаемым поршнем, который может скользить без трения. В верхней половине находится m₁ граммов водорода при температуре Т₁, нижней части – m₂ граммов кислорода при температуре Т₂. Сосуд перевернул. Чтобы поршень по-прежнему делил сосуд на две равные части, водород пришлось нагреть до температуры Т₃. Температура кислорода осталась прежней. Определить, до какой температуры необходимо было нагреть водород и каково давление водорода в первом и втором случаях если вес поршня – Р, его сечение – S.

2.12. Абсолютное давление азота в сосуде при комнатной температуре (Г = 20º) р = 2,2 МПа. В сосуде азот нагревают, причем известно, что предельное избыточное давление, при котором возможна безопасная работа р_изб = 6 МПа. Определить температуру, до которой возможно нагревание азота. Барометрическое давление В = 1000 гПа.

2.13. Определить плотность воздуха и водорода при нормальных условиях.

2.14. Определить для азота и водорода коэффициент изотермического сжатия , если эти газы находятся при параметрах р = 1,2 МПа и t = 430ºС.

2.15. Определить численное значение коэффициента теплового расширения α =  и термического коэффициента давления  для кислорода и окиси углерода, если эти газы находятся при параметрах р = 1,2 МПа и t = 430ºC.

2.15. Определить удельный объем кислорода при давлении 2,3 МПа и температуре 280ºС. Задачу решить в Международной системе единиц.

2.16. Определить массу воздуха, находящегося в комнате площадью 25 м² высотой 3,2 м. Принять, что температура воздуха в комнате t = 22ºС, а барометрическое давление В = 986,5 гПа.

2.17. Определить плотность азота при давлении 1 и 6 МПа. Температура азота t = 400ºС.

2.18. Чему равна плотность воздуха при параметрах t = 20ºС и р = 1,5 МПа?

2.19. Давление водяных паров в воздухе комнаты равно 2 кПа. Сколько содержится водяного пара в комнате? Площадь комнаты 25 м², высота 3 м, температура воздуха 25ºС.

Стоимость: 60 руб

2.20. В комнате площадью 35 м² и высотой 3,1 м воздух находится при t = 23ºС и барометрическом давлении В = 973 гПа. Какое количество воздуха проникнет с улицы в комнату, если барометрическое давление увеличится до В = 1013 гПа? Температура воздуха остается постоянной.

2.21. При измерении расхода воздуха с помощью дроссельной шайбы было зафиксировано, что при р = 1000 гПа и t = 20ºС расход воздуха равен 24 дм³/мин. Определить массовый расход воздуха в килограммах в минуту и объемный расход в кубических метрах в минуту при нормальных условиях.

2.22. Производительность воздушного компрессора при нормальных условиях V_к = 500 м³/ч. Чем равна массовая производительность компрессора?

2.23. 0,03 м³ кислорода, отнесенного к нормальным условиям находится в сосуде емкостью 650 см³. Определить показания манометра, измеряющего давление в этом сосуде, если температура кислорода t = 200ºС. Атмосферное давление В = 1016 гПа.

2.24. Компрессор подает кислород в резервную емкостью 3 м³, избыточное давление в резервуаре увеличивается при этом от 0,01 до 0,6 МПа а температура газа – от 15º до 30ºС. Определить массу поданного компрессором кислорода. Барометрическое давление В = 993 гПа.

2.25. Масса пустого баллон для аргона емкостью 40 дм³ равна 64 кг. Определить массу баллона с аргоном, если при температуре t = 15ºС баллон наполняют газом до давления р = 15 МПа. Как изменится давление аргона, если баллон внести в помещение с температурой t = 25ºС?

Стоимость: 90 руб

2.26. В сосуде объемом 5 м³ находится воздух при барометрическом давлении В = 0,1 МПа и температуре 300ºС. Затем воздух выкачивается до тех пор, пока в сосуде не образуется вакуум, равный 80 гПа. Температура воздуха после выкачивания остается той же. Сколько воздуха выкачано? Чему будет равно давление в сосуде после выкачивания, если оставшийся воздух охладить до температуры t = 20ºС?

2.27. В большой сосуд с водой опрокинут стеклянный стакан (рис. П.1.7). Уровень воды внутри и вне стакана одинаков. Расстояние от дна стакана до уровня воды равно l. Температура воздуха – Т₁, атмосферное давление – р₀. На какую высоту изменится уровень воды в стакане при понижении температуры до Т₂ и повышении атмосферного давления до р₀₂? Изменением уровня воды в сосуде пренебречь.

2.28. Оболочка воздушного шара с массой m и объемом V, на 8/9 наполнена водородом при температуре Т₁ и давлении р₁. Какая масса водорода выйдет из оболочки и как изменится подъемна сила водорода, наполняющего оболочку, на высоте, где давление и температура равны р₂ и Т₂ (при подъеме водород может выходить через отверстие в нижней части оболочки)?

2.29. Цилиндрический сосуд с газом разделен поршнем на две камеры. Состояние газа в обеих камерах характеризуется соответственно параметрами р₁, V₁, Т₁ и р₂, V₂, Т₂. При каком давлении поршень будет находиться в равновесии, если его освободить, газ в первой камере нагреть, а во второй – охладить на ΔТ (нагревом поршня пренебречь)?

2.30. Два сосуда, содержащие одинаковые массы одного газа соединены трубкой с краном. В первом сосуде давление р₁ = 5 · 10³ Н/м², во втором – р₂ = 8 · 10³ Н/м². Какое давление установится после открытия крана, если температура останется неизменной?

2.31. Средняя квадратичная скорость молекул некоторого газа ν_с.м = 450 м/с. Давление газа р = 7 · 10⁴ Н/м². Найти плотность газа ρ при этих условиях.

2.32. В сосуде находится V = 2 · 10^{-3 м3} воды при температуре t = 47ºС. Найти давление внутри сосуда при условии, что силы взаимодействия между молекулами внезапно исчезли.

2.33. В дне сосуда, из которого выкачан воздух до давления р₁, проделано малое отверстие. С какой скоростью начнет врываться в сосуд воздух, если атмосферное давление – р₀ и плотность воздуха ρ (рис. П.1.8).

2.34. При температуре t = 207ºС масса m = 2,5 кг некоторого газа занимает объем V = 0,3 м³. Определить давление газа, если удельная теплоемкость с_р = 519 Дж/(кг · К) и γ = 1,67.

2.35. Некоторый газ при нормальных условиях имеет плотность р = 0,0894 кг/м³. Определить его удельные теплоемкости с_р, с_ν, а также найти, какой это газ?

 3. 1-й закон термодинамики

3.1. При испытании двигателей для определения мощности необходимо их тормозить (рис. П.1.9). При этом работа, произведенная двигателем, расходуется на преодоление сил трения и превращается в теплоту, часть которой (примерно 20%) рассеивается в окружающей среде, а остальная часть отводится охлаждающей тормоз водой. Сколько воды необходимо подводить к тормозу за 1 ч, если крутящий момент на валу М_кр = 2000 Дж, частота вращения n = 1500 об/мин, а допустимое повышение температуры воды ΔТ = 35 К? Теплоемкость воды принять равной 4,1868 кДж/(кг · К).

3.2. Проводится испытание двигателя, во время которого двигатель вместо того, чтобы принимать полезную нагрузку, тормозится. На сколько градусов нагреется охлаждающая тормоз вода, если крутящий момент двигателя равен 5 кДж, а частота вращения – 1500 об/мин? Известно, что к колодкам тормоза, подводится 10 т/ч воды при температуре 15ºС. Предполагается, что вся работа двигателя превращается к теплоту трения.

3.3. Какое количество охлаждающей воды следует подавать на колодки испытательного тормоза в 1 ч, если мощность двигателя 55 кВт, температура охлаждающей воды 10ºС, а предельно допустимая температура воды на выходе 80ºС? Часть теплоты трения (20%) рассеивается в окружающей среде.

3.4. При торможении двигателя охлаждающая тормозные колодки вода нагревается на 30 К. Расход воды m_в = 1500 кг/ч. Определить мощность двигателя, если 25% теплоты трения рассеивается в окружающей среде.

3.5. Испытание двигателя ведется при помощи присоединенного к нему генератора. Напряжение на клеммах генератора постоянного тока u = 220 В, сила тока l = 50 А, к.п.д. генератора η_г = 0,98. Определить мощность двигателя на валу.

3.6. Определить к.п.д. двигателя автомобиля мощностью 44,0 кВт при расходе топлива 7,4 кг/ч. Теплоту сгорания топлива  принять равной 40 МДж/кг.

3.7. Мощность электростанции на выходных шинах составляет 12 МВт. Какое количество топлива В, кг/ч, сжигается в топках котлов электростанции, если все потери энергии на станции составляют 70%, а теплота сгорания топлива = 30 МДж/кг.

Стоимость: 60 руб

3.8. На электростанции мощностью N = 100 МВт сжигается топлива с теплотой сгорания  = 30 МДж/кг. Коэффициент полезного действия станция η= = 33,0%. Определить часовой расход топлива В.

3.9. Паровая турбина расходует 0,00110 кг пара на получение 1 кДж электроэнергии. На производство 1 кг пара необходимых параметров затрачивается 3300 кДж. Определить к.п.д. паротурбинной установки.

3.10. Определить термический к.п.д. четырехпроцессного цикла, если работа и теплота, участвующие в каждой процессе равны,

Процесс	1	2	3	4
l, кДж/кг	3	10	-8	0
q, кДж/кг	30	-10	-20	5

Стоимость: 60 руб

3.11. Состояние газа под поршнем цилиндра определяется точкой l на рис. П.1.10. Газ переводится в состояние 2 один раз по пути 1 а 2 и второй – по пути 1 b 2. Определить будут ли отличаться в этих процессах количества подведенной и отведенной теплоты и если да, то насколько. Известно, что давления в точках 1 и 2 равны 0,1 и 0,5 МПа соответственно, а изменение объема V₂ – V₁ = 0,5 м³.

3.12. Какова стоимость энергии, необходимой для того, чтобы поднять 1 т оборудования на вершину телевизионной башни высотой 516 м, если цена электроэнергии составляет 2 коп/(кВт · ч), а к.п.д. подъемного механизма η = 0,85?

3.13. В процессе расширения давление и объем идеального газа связаны соотношением рν^k = const, где k = 1,4. Показать, что работа расширения от р₁, ν₁ до р₂, ν₂ определяется уравнением l =  (р₁ν₁ – р₂ν₂), и вычислить ее, если р₁ = 1,2 МПа, ν₁ = 0,1 м³/кг и р₂ = 0,2 МПа, ν₂ = 0,360 м³/кг.

3.14. В канале произвольной формы (рис. П.1.11) течет воздух в количестве 5 кг/с. На входе в канал энтальпия газа, скорость потока и высота входного сечения над произвольной горизонтальной плоскостью соответственно равны h₁ = 293 кДж/кг, ω₁ = 30 м/с х₁ = 30 м, на выходе из канала h₂ = 300 кДж/кг, ω₂ = 15 м/с, х₂ = 10 м. Протекая в канале, газ получает извне энергию в форме теплоты в количестве 30 кДж/с. Какую техническую работу совершает поток газа?

3.15. Воздушный компрессор сжимает 129 кг/ч воздуха. Установлено, что при сжатии энтальпия воздуха увеличивается на 17 МДж/ч, а энтальпия охлаждающей компрессор воды – на 10 МДж/ч. Пренебрегая потерями и изменением кинетической и потенциальной энергии найти мощность привода компрессора.

3.16. Газ, состояние которого определяется на р, ν – диаграмме (рис. П.1.12) точкой l, переводится в состояние 2 по пути 1 с 2. При этом к газу подводится 8 кДж энергии в виде теплоты и от газа получается 30 кДж работы. Затем этот же газ возвращается в исходное состояние в процессе, который описывается кривой 2 а 1. Сколько энергии нужно подвести в некотором другой процессе 1 d 2, чтобы от газа получить 10 кДж работы? Сколько нужно подвести или отвести теплоты в процессе 2 а 1, если на сжатие расходуется 50 кДж энергии в форме работы?

3.17. Газ, имеющий массу m = 1 кг, находится под поршнем цилиндра в состоянии (рис. П.13) с параметрами р₁ = 0,5 МПа и ν₁ = 0,100 кг/м³. Он может перейти в состояние 2 с параметрами р₂ = 0,1 МПа и ν₂ = 0,262 кг/м³ посредством процесса 1 а 2 или 1 b 2. Процесс 1 а 2 протекает без теплообмена, его уравнение р = сν-^5/3. Процесс 1 b 2 характерен тем, что при его осуществлении теплота сначала подводится к газу, а затем отводится от него. В процессе 1 b 2 давление зависит от объема линейно. Определить работу, которую совершает газ, если происходит процесс 1 а 2. Какое количество теплоты, подведенное к газу в процессе 1 b 2 или отведенное, больше по своему абсолютному значению и насколько?

3.18. Центробежный компрессор сжимает 100 кг/ч азота. При сжатии энтальпия азота увеличится на 200 кДж/кг. Какова должна быть мощность привода компрессора, если теплообменом с окружающей средой и изменением кинетической и потенциальной энергии сжимаемого азота пренебречь?

4. Газовые смеси. Процессы изменения состояния газа

4.1. В закрытом сосуде емкостью V = 2 м³ находится m₁ = 2,7 кг воды и m₂ = 3,2 кг кислорода. Найти давление в сосуде при температуре t = 527ºС, зная что в этих условиях вся вода превращается в пар (считать, что пар в данном случае подчиняется законам идеального газа).

4.2. Найти плотность воздуха при давлении р₀ = 1 · 10⁵ Па и температуре t = 13ºС, считая что в воздухе содержится 23,6 вес. % кислорода (О₂) и 76,4 вес. % азота (N₂). Найти парциальные давления кислорода и азота при этих условиях.

4.3. В сосуде находится смесь азота и водорода. При температуре Т, когда азот полностью диссоциирован на атомы, давление равно р (диссоциацией водорода пренебречь). При температуре 3Т, когда оба газа полностью диссоциированы, давление в сосуде равно 4р. Каково отношение масс водорода и азота в смеси?

4.4. Газ с массой m₁ и молекулярным весом μ₁ смешали с газом, масса которого равна m₂, а молекулярный вес – μ₂. Найти кажущийся молекулярный вес смеси.

4.5. Определить плотность смеси газа и кажущийся вес смеси, состоящей из m₁ кислорода, m₂ водорода и m₃ углекислого газа, при температуре Т и давлении р.

4.6. Газ массой m = 15 кг, молекулы которого состоят из атомов водорода и углерода, содержит N = 5,64 · 10²⁶ молекул. Определить массу атомов углерода и водорода, входящих в молекулу этого газа.

4.7. Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.

4.8. Какое число молекул двихатомного газа содержится в сосуде объемом V = 20 см³ при давлении р = 1,05 · 10⁴ Па и температуре t = 27ºС? Какой энергией теплового движения обладают эти молекулы?

4.9. Определить число молекул в 1 мм³ воды; массу молекулы воды; диаметр молекулы воды, считая условно, что молекулы воды шарообразны и соприкасаются.

4.10. Найти отношение с_р/с_ν смеси газов, состоящей из m₁ = 20 г гелия и m₂ = 8 г водорода.

4.11. Разность удельных теплоемкостей некоторого двухатомного газа с_р – с_ν = 260 Дж/(кг · К). Найти массу одного киломоля газа и его удельные теплоемкости.

4.12. Плотность смеси азота и водорода при температуре t = 47ºС и давлении р = 2,03 · 10⁵ Па равна ρ = 0,3 кг/м³. Какова концентрация молекул водорода в смеси?

4.13. Смесь идеальных газов состоит из m₁ кг газа 1, m₂ кг газа 2 и m₂ кг газа 3. Определить чему равно давление смеси, если объем смеси газов равен V_см, а температура смеси Т_см.

4.14. Смесь 10 кг кислорода и 15 кг азота имеет давление ,3 МПа и температуру 27ºС. Определить, мольные доли z₁ каждого газа в смеси, кажущуюся молекулярную массу смеси, удельную газовую постоянную, общий объем смеси, парциальные давления и объемы.

4.15. В сосуде находится смесь состоящая из одного киломоля кислорода и двух киломолей азота при р₁ = 0,1 МПа и t₁ = 30ºС. Эта смесь охлаждается при постоянном объеме до температуры t₂ = 10ºС. Определить изменение внутренней энергии смеси.

Стоимость: 90 руб

4.16. Воздух, если считать, что он является смесью только азота и кислорода, имеет следующий объемный состав: = 79,0%; = 21,0%. Определить массовые доли азота и кислорода в воздухе, вычислить газовую постоянную воздуха.

4.17. Воздух объемом 0,3 м³ смешивается с 0,5 кг углекислого газа. Оба газа до смешения имели параметры р = 0,5 МПа и t = 45ºС. Определить парциальное давление углекислого газа.

4.18. Дымовые газы имеют следующий массовый состав:  = 16,1%;  = 7,5%;  = 76,4%. Рассчитать энтальпию k_см этих газов, отнесенную к 1 кг смеси при t = 800ºС и отсчитанную от 0ºС.

4.19. Рассчитать истинную теплоемкость с_р смеси паров двуокиси углерода и воды. Массовая доля двуокиси углерода  = 0,9383. Расчет произвести, пользуясь таблицами приложения 2 для температур 200º и 400ºС.

4.20. Энергетические установки, работающие по парогазовому циклу, в качестве рабочего тела используют смесь водяного пара и горячих продуктов сгорания топлива. Массовая доля продуктов сгорания топлива g = 0,7. Принять, что продукты сгорания обладают свойствами воздуха. Определить теплоемкость ср смеси при температурах 500 и 800ºС, а также удельный объем смеси при р = 0,1 МПа и t = 500ºС (таблицы приложения 2).

4.21. В сосуде находится смесь газов, образовавшаяся в результате смешения 10 кг азота, 3 кг аргона и 27 кг двуокиси углерода. Определить мольный состав смеси, ее удельный объем при нормальных условиях, кажущуюся мольную массу смеси газовую постоянную, отнесенную к одному кубическому метру при нормальных условиях.

4.22. Влажный воздух представляет собой смесь сухого воздуха и водяного пара. Известно, что на каждый килограмм сухого воздуха во влажном воздухе содержится d г водяного пара. Определить массовые и объемные доли сухого воздуха и водяного пара, плотность при нормальных условиях, газовую постоянную, отнесенную к 1 кг, и кажущуюся мольную массу смеси, если d = 10 г/кг сухого воздуха.

4.23. Объемный состав горючего газа:  = 10%;  = 45%;  = 35%;  = 4%;  = 3%;  = 3%. Определить кажущуюся мольную массу, плотность, удельный объем при нормальных условиях, массовую газовую постоянную R, парциальное давление метана в процентах и массовые доли содержания компонентов.

4.24. Смесь газов, образовавшихся при сжигании 1 кг мазута в топке парового котла, имеет состав, определенный парциальными объемами составляющих: = 1,85 м³;  = 0,77 м³;  = 12,78 м³. Определить массовые доли и парциальные давления составляющих, если общее давление р = 0,1 МПа.

4.25. Сосуд разделен перегородкой на две части, объемы которых V₁ = 1,5 м³ и V₂ = 1,0 м³. В части объемом V₁ содержится двуокись углерода при р₁ = 0,5 МПа и t₁ = 30,0ºС, а в части объемом V₂ – кислород при р₂ = 0,2 МПа и t₂ = 57ºС. Определить массовые и объемные доли двуокиси углерода и кислорода, кажущуюся молекулярную массу смеси и ее газовую постоянную после того, как перегородка будет убрана и процесс смешения закончится (рис. П.1.14).

4.26. Имеются два сосуда, соединенных между собой трубкой, на которой установлен кран, разобщающий их. В первом сосуде, емкость которого V₁ = 2 м³, находится воздух при р₁ = 1,0 МПа и t₁ = 27ºС. Второй (V₂ = 1 м) содержит также воздух при р₂ = 0,2 МПа и t₂ = 57ºС. Кран при этом закрыт. Затем кран открывается и система приходит в равновесное состояние. Определить давление и температуру образовавшейся смеси. Теплоемкость считать не зависящей от температуры.

4.27. Образование смеси двух газов – азота и гелия – происходит так же, как и в задаче 4.25. Состояние газов до смешения.

Наименование	N2	He2
Масса m, кг	10	5
Объем V, м3	1,5	1,0
Температура t, ºС	120	860

Найти давление и температуру смеси, объемные доли компонентов, а также парциальные давления азота и гелия после окончания процесса смешения. Предполагается, что теплоемкости не зависят от температуры; их следует рассчитать по формуле молекулярно-кинетической теории. Теплообмен со средой отсутствует.

4.28. При температуре t = 207ºС m = 2,5 кг некоторого газа занимает объем V = 0,3 м³. Определить давление газа, если удельная теплоемкость с_р = 519 Дж/(кг · К) и γ = 1,67.

4.29. Некоторый газ при нормальных условиях имеет плотность ρ = 0,0894 кг/м³. Определить его удельные теплоемкости с_р с_μ а также найти, какой это газ.

4.30. На рис. П.1.15 изображен график изменения состояния идеального газа в координата рV. Представить этот круговой процесс в координатах рТ и VТ, обозначив соответствующие точки.

4.31. Некоторое количество идеального газа совершает замкнутый процесс 1 – 2 – 3 – 1, который изображен на графике зависимости объема от температуры (рис. П.1.16). Изобразить этот процесс в координатах РV и указать, на каких стадиях процесса газ получал, а на каких – отдавал тепло.

4.32. При нагревании газа были получены графики зависимости давления (рис. П.1.17 а) и объема (рис. П.1.7 б) от абсолютной температуры. Как изменились в первом случае объем, а во втором – давление?

4.33. Два сосуда, содержащие одинаковые массы одного газа, соединены трубкой с краном. В первом сосуде давление р₁ = 5 · 10³ Н/м², во втором – р₂ = 8 · 10³ Н/м². Какое давление установится после открытия крана, если температура останется неизменной?

5. 2-й закон термодинамики

5.1. Количество азота, находящегося в сосуде под поршнем равно m. Вес поршня – Р, площадь его поперечного сечения – S. Атмосферное давление – р₀. Сколько теплоты нужно тратить, чтобы нагреть газ на Δt? Насколько при этом поднимется поршень?

5.2. При изобарическом расширении двухатомного газа была совершена работа А. Какое количество теплоты сообщено газу?

5.3. Масса m идеального газа, находящегося при температуре Т, охлаждается изохорически так, что его давление уменьшается в n раз. Затем газ расширяется при постоянном давлении. Температура газа в конечном состоянии равна первоначальной. Определить совершенную газом работу. Молекулярная масса газа μ.

5.4. Один моль идеального газа совершает замкнутый процесс, состоящий из двух изохор и двух изобар (рис. П.1.18). Температура в точке 1 равна Т₁, в точке 3 – Т₃. Определить работу, совершаемую газом за цикл, если точки 2 и 4 лежат на одной изотерме.

5.5. При адиабатическом расширении азота с массой m совершается работа А. Насколько уменьшилась внутренняя энергия и понизилась температура азота, если его удельная теплоемкость при постоянном объеме равна с_γ?

5.6. Каковы были начальные объем и температура массы m гелия, заключенного под поршнем в цилиндр, если при охлаждении его до 0ºС потенциальная энергия груза весом Р, лежащего на поршне, уменьшилась на ΔЕ. Площадь поршня – S, атмосферное давление – р₀.

5.7. В закрытом сосуде находятся массы m₁ азота и m₂ кислорода. Найти изменение внутренней энергии смеси при охлаждении ее на ΔТ.

5.8. Двухатомный газ с массой m, имеющий молекулярную массу μ, находится в закрытом сосуде под давлением р при температуре Т. После нагревания давление в сосуде стало равно р₁. Какое количество теплоты было сообщено газу при нагревании?

5.9. Найти молекулярную массу и первоначальный удельный объем газа подвергшегося изотермическому сжатию, если в конце сжатия давление массы m газа увеличилось в n раз и произведенная работа равна А. До сжатия газ находится под давлением р₁ при температуре Т₁.

5.10. Атомарный кислород О, молекулярный кислород О₂, и озон О₃ отдельно друг от друга расширяются изобарически. При этом расходуется количество ΔQ теплоты. Определить доли теплоты, расходуемые на расширение и изменение внутренней энергии для О, О₂, О₃.

5.11. Масса m = 2 г гелия, находящегося при t = 0ºС и давления р = 2 · 10⁵ Н/м², изотермически расширяется за счет полученного извне тепла до объема ν = 2 л. Найти работу, совершенную газом при расширении; количество сообщенной газу теплоты.

5.12. Определить изменение энтропии 3 кг азота в политропном процессе при изменении температуры от t₁ = 100ºС до t₂ = 300ºС. Показатель политропы n = 1,2. Теплоемкости принять по молекулярно-кинетической теории. Изобразить процесс в ш – ν и Т— s – диаграммах.

5.13. Определить изменение энтропии 1 кг двуокиси углерода в процессе сжатия. Начальные параметры углекислоты: t₁ = 40ºС, р₁ = 0,2 МПа, конечные: t₂ = 253ºС, р₂ = 4,5 МПа. Расчет сделать в двух вариантах: 1) при расчете теплоемкости углекислого газа использовать молекулярно-кинетическую теорию; 2) применять при расчете табл. 1 приложения  с учетом зависимости теплоемкости от температуры.

Стоимость: 90 руб

5.14. 1 кг азота и 1 кг водорода сжимаются изотермически при t = 15ºС от 0,1 до 1 МПа. Для какого газа изменение энтропии будет больше и во сколько раз (по отношению к изменению энтропии другого газа)?

5.15. Построить в Т – s координатах изобары воздуха в пределах от 0º до 1500ºС, соответствующие 0,01; 0,1 и 1 МПа, приняв значение энтропии воздуха равным нулю при t = 0ºС и р = 0,1 МПа. Построение произвести по точкам, отстоящим на 300ºС друг от друга.

5.16. Определить изменение энтропии в процессе испарения 1 кг воды при температуре, равной 100ºС, если известно, что теплота парообразования r = 2257 кДж/кг.

5.17. 50 кг льда с начальной температурой – 5ºС помещены в воздух с температурой +15ºС. Считая, что образующаяся при таянии вода нагреется до температуры воздуха, определить увеличение энтропии, происходящее в результате этого процесса. Теплота таяния льда λ = 333 кДж/кг, теплоемкость льда с_р = 2,03 кДж/(кг · К). Теплоемкость воды принять равной 4,187 кДж/(кг · К).

5.18. 30 л воды с температурой 90ºС смешиваются с 20 л воды с температурой 15ºС. Определить вызванное этим процессом изменение энтропии. Теплоемкость воды принять равной 4,187 кДж/(кг · К). Считать, что тепловые потери отсутствуют.

5.19. Стальной шар массой 10 кг при 500ºС погружается в сосуд с 18 кг воды, температура которой равна 15ºС. Определить изменение энтропии системы в этом процессе. Считать, что тепловые потери отсутствуют. Теплоемкость стали принять равной 0,5129 кДж/(кг · К), теплоемкость воды 4,187 кДж/(кг · К).

5.20. Определить энтропию 1 кг газовой смеси, состоящей из азота и аргона, при р₀ = 0,3 МПа и t₀ = 300ºС. Массовые доли азота и аргона:  = 0,37,  = 0,63. Газы считать идеальными. Принять, что при р₀ = 0,1 МПа и t₀ = 0ºС энтропия азота и аргона равна нулю. Для расчета использовать таблицы приложения 2.

5.21. Определить, насколько увеличится энтропия при смешение 3 кг азота и 2 кг углекислого газа. Газы считать идеальными. Температура и давление газов до смешения одинаковы.

5.22. Смесь газов из 70% азота и 30% водорода (по массе) находится при t = 600ºС и р = 0,2 МПа. Вычислить энтропию 1 кг смеси. Считать, что энтропия обоих компонентов при t₀ = 0ºС и р₀ = 0,1 МПа равна нулю. При расчете воспользоваться таблицами приложения 2. Считать, что между азотом и водородом не происходит химической реакции.

6. Циклы тепловых и холодильных машин

6.1. Компрессор захватывает при каждом качании V₀ = 5 · 10^{-3 м3} воздуха при нормально атмосферном давлении р₀ и температуре t₀ = -3ºС и нагнетает его в резервуар емкостью V = 2 м³, причем температура воздуха в резервуаре поддерживается равной t = — 53ºС. Сколько качаний должен сделать компрессор, чтобы давление в резервуаре увеличилось на Δр = 4 · 10⁵ Па?

6.2. На рис. П.1.19 показана теоретическая диаграмма работы компрессора двойного действия. Участок 1 – 2 соответствует изотермическому сжатию; участок 2 – 3 – проталкиванию воздуха в резервуар (р = const); на участке 3 – 4 происходит мгновенное уменьшение давления в цилиндре компрессора при закрытии выпускного клапана.

6.3. Газ совершает цикл Карно. Абсолютная температура нагревателя в n раз выше абсолютной температуры охладителя. Какую долю теплоты, получаемой за один цикл от нагревателя, газ отдает охладителю?

6.4. От идеальной теплосиловой установки, работающей по циклу Карно, отводится ежечасно с помощью холодильника количество теплоты Q’₂ при температуре Т₂. Определить мощность установки, если количество подводимой теплоты равно Q’₁. При какой температуре подводится тепло?

6.5. Идеальная холодильная машина работающая по обратному цикл Карно, передает тепло от холодильника с водой при температуре Т₂ кипятильнику с водой при температуре Т₁. Какое количество воды m₁ нужно заморозить в холодильнике, чтобы превратить в пар воду с массой m₂ в кипятильнике?

6.6. Определить термический к.п.д. теплового двигателя, работающего по обратному циклу Карно. Температура подвода тепла 500ºС, температура отвода тепла 20ºС. Определить также, сколько поводится и сколько отводится теплоты в этом двигателя, если его мощность N = 5 МВт.

6.7. Холодильная установка холодопроизводительностью 6000 ккал/ч создает температуру в охлаждаемом помещения t = -10ºС. Температура помещения, в котором стоит холодильная установка, равна 20ºС. Приняв, что холодильная установка работает по обратному циклу Карно, определить холодильный коэффициент ε, количество теплоты q’, которое передает установка верхнему тепловом источнику (среде) в процессе при t = 20ºС и теоретическую мощность привода установки. Определить будет нагреваться или охлаждаться помещение после включении холодильной установки, и количество теплоты q’’, которое будет подводиться (или отводиться) к воздуху в комнате.

6.8. Идеальный поршневой компрессор сжимает 450 м³/ч воздуха (в пересчете на нормальные условия) температурой t₁ = 30ºС от р₁ = 0,10 МПа и до р₁ = 0,5 МПа. Определить мощность, затрачиваемую на привод компрессора, если сжатие происходит адиабатично, и температуру газа на выходе из компрессора.

6.9. Компрессор сжимает 600 м³/ч воздуха от давления р₁ = 0,098 МПа до р₂ = МПа.  Определить мощность, необходимую на приводе компрессора, если сжатие происходит: 1) адиабатно; 2) политропно с показателем n = 1,3; 3) изотермически.

6.10. Многоступенчатый поршневый компрессор без вредного объема сжимает воздух от начального давления р₁ = 0,0981 МПа до давления р₂ = 5,4 МПа. Известно, что отношение конечного давления к начальному одинаков для всех цилиндров и находится в пределах 6 – 8. Определить число ступеней в компрессор, мощность двигателя, если к.п.д. ступени равен 0,7, и расход охлаждающей воды при увеличении ее температуры на 15ºС. Известно, что начальная температура воздуха t₁ = 17ºС, а сжатие политропическое с показателем n = 1,3. Производительность компрессора 300 м³/ч (в пересчете на нормальные условия).

6.11. Двухступенчатый поршневой компрессор сжимает воздух от давления р₁ = 0,0981 МПа до давления р₂ = 5,88 МПа. Сжатие политоропное с показателем n = 1,25. Начальная температура воздуха t₁ = 20ºС, производительность компрессора 500 м³/ч. Определить расход охлаждающей воды на охлаждение цилиндров и промежуточного холодильника, если ее температура возрастает от 10 до 30ºС, а также мощность двигателя на привод компрессора, если η_k = 0,65. Компрессор без вредного объема.

6.12. В двухступенчатом компрессоре без вредного объема воздух адиабатически сжимается от 0,098 до 4,9 МПа. Определить производительность компрессора в пересчете на нормальные условия, если мощность его двигателя 60 кВт, к.п.д. компрессора η_k = 0,65. Начальная температура воздуха 27ºС.

6.13. В изотермическом компрессоре воздух сжимается от 0,098 до 0,981 МПа. Как изменится мощность двигателя для привода компрессора, если сжатие будет производиться изотермически до 98,1 МПа.

6.14. Определить объемную часовую производительность по сжатому воздуху компрессора, сжимающего воздух от р₁ = 0,098 МПа и t₁ = 15ºС до р₂ = 0,784 МПа. Сжатие изотермическое, мощность двигателя 40 кВт.

6.15. В результате уменьшения расхода воды, охлаждающей цилиндр компрессора, температура сжатого воздуха на выходе из компрессора возрастает от 100 до 150ºС. Начальная температура воздуха остается постоянной и равной 17ºС. Давление сжатого воздуха р₂ = 0,5 МПа, начальное давление р₁ = 0,91 МПа. Как изменится затрачиваемая мощность? Сжатие политропное.

6.16. Турбокомпрессор адиабатно сжимает 500 м³/ч воздуха от р₁ = 0,1 МПа и t₁ = 20ºС до р₂ = 0,4 МПа. Адиабатный к.п.д. компрессора η_од = 0,85. Определить конечную температуру сжатия и затраченную на сжатие работу. Расчет произвести при помощи таблиц приложения 2.

6.17. Кислородный компрессор сжимает кислород от р₁ = 0,098 МПа t₁ = 17ºС до давления 0,4 МПа. Определить необходимую мощность двигателя, если адиабатный к.п.д. установки η_од = 0,83. Производительность компрессора равна 200 м³/ч сжатого газа.

6.18. Рассчитать термический к.п.д. простейшей газотурбинной установки, работающей по циклу с подводом теплоты при р = const и при следующих степенях повышения давления 1) β₁ = 5; 2) β₂ = 10; 3) β₃ = 20. Считать, что рабочее тело обладает свойствами воздуха. Показатель адиабаты принять равным k = 1,4.

6.19. Газотурбинная установка (ГТУ) работает по циклу с подводом теплоты при р = const. Степень повышения давления β = 12. Рассчитать термически к.п.д. ГТУ для двух случаев: 1) рабочим телом является воздух; 2) рабочим телом является гелий.

6.20. Компрессор газотурбинной установки сжимает воздух с начальными параметрами р₁ = 0,1 МПа и t₁ = 5ºС до давления р₂ = 0,8 МПа. Внутренний относительный к.п.д. компрессора равен 0,84. Определить температуру воздуха на выходе из компрессора и также мощность привода компрессора N₁, если известно, что компрессора должен подавать 1 · 10⁵ кг/ч воздуха.

6.21. В турбину газотурбинной установки входит гелий с параметрами р₃ = 1,0 МПа; t₃ = 700ºС. Внутренний относительный к.п.д. турбины равен 0,86, давление за турбиной р₄ = 0,1 МПа. Определить температуру гелия на выходе из турбины. Рассчитать также массовый часовой расход гелия D, если действительная мощность турбины N_Т = 40 МВт. При решении задач этого раздела считать, что рабочее тело обладает свойствами идеального газа.

Часть задач есть решенные, контакты