Р.54
Задач, которых нет, Вы можете заказать
Задача 1.1а
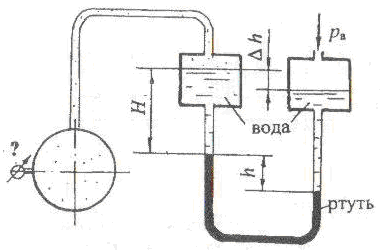
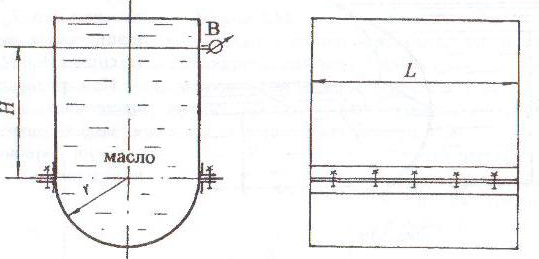
Два сосуда наполнены разнородными жидкостями – маслом и керосином. На поверхности жидкостей в сосудах действует давление р1 и р2 (рис. 1.1).
Найти разность этих давлений ∆р, если показание U-образного ртутного манометра h, высота уровня масла H, превышение уровня керосина над водой ∆h. Принять плотности жидкостей:
масла ρмасл = 900 кг/м3;
керосина ρкер = 800 кг/ м3;
ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.1а
Задача 1.2а
В закрытом резервуаре А, заполненным маслом, давление на поверхности жидкости p0 (рис. 1.2). На глубине h подключен U-образный ртутный манометр, показание которого hрт, понижение уровня ртути в правом колене a. Определить давление p0 (в бар) на поверхности масла, а также высоту подъема hв в стеклянной трубке, опущенной в открытый резервуар В, заполненный водой.
Принять плотности: масла ρмас = 900 кг/м3; ртути ρрт = 13,6 · 103 кг/м3; воды ρрт = 103 кг/м3.
Купить задачу 1.2а
Задача 1.3а
Определить, каким прибором (манометром или вакуумметром) следует измерить давление газа в баллоне по показанию h двухжидкостного чашечного манометра, заполненного водой и ртутью (рис. 1.3), если высота столба воды в левом колене манометра H; разность уровней воды в чашках манометра Δh.
Принять плотности жидкостей: воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3. Плотность газа можно не учитывать. Показание прибора представить в ат.
Купить задачу 1.3а
Задача 1.4а
Определить давление рx (в бар) в центре сосуда с бензином (рис. 1.4), если показание манометра, включённого на уровне центра сосуда с водой, pман, высоты уровней жидкостей: h1 и h2 .
Центры резервуаров находятся на одном уровне. Принять плотности жидкостей: бензина ρбенз = 720 кг/м3; ртути ρрт = 13,6 · 103 кг/м3; воды ρ = 103 кг/м3.
Купить задачу 1.4а
Задача 1.5а
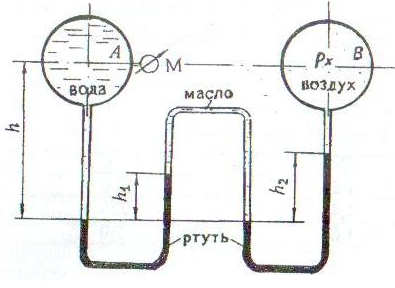
Определить абсолютное давление воздуха в резервуаре В (рис. 1.5), если показание манометра, установленного по центру резервуара А, заполненного маслом, рман, высоты уровней масла и ртути в U-образном ртутном манометре соответственно hм и hрт.
Плотности: масла ρмасл = 900 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.5а
Задача 1.6б
Два резервуара А и В, линии центров которых совпадают, соединены двухколенным ртутным манометром (рис 1.6).
Определить показание манометра на поверхности воды в резервуаре А, если абсолютное давление воздуха в резервуаре B – рабс, высоты уровней ртути в дифференциальном манометре h1 и h2. Уровень ртути в левом колене расположен ниже уровня воды в резервуаре A на величину h. Пространство между уровнями ртути в манометре заполнено маслом плотностью ρмасл = 880 кг/м3. Плотность ртути ρрт = 13,6 · 103 кг/м3; воды ρ = 103 кг/м3. Плотностью воздуха при расчётах можно пренебречь.
Купить задачу 1.6б
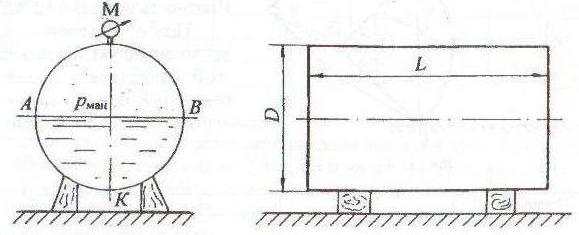
Задача 1.7а
Определить абсолютное давление на поверхности бензина в закрытом резервуаре (pабс) (рис. 1.7), а также показание мановакуумметра (pмв в бар), установленного на глубине h1 при заданных величинах h и hрт. Атмосферное давление pа = 740 мм рт. ст. Плотность жидкостей: бензина ρбенз = 720 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Давление воздуха в U-образном ртутном манометре не учитывать.
Купить задачу 1.7а
Задача 1.8а
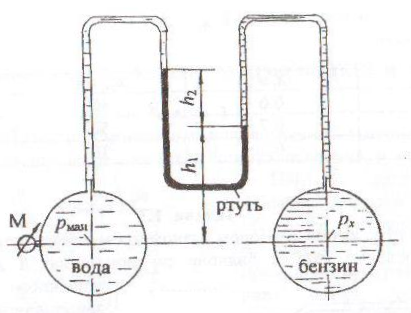
Дифференциальный манометр, заполненный ртутью, предназначен для измерения разности давлений на уровне осей трубопроводов А (pA) и В (pB), транспортирующих воду и бензин. Оси трубопроводов находятся на одном горизонте (рис. 1.8).
Определить разность давлений в кПа по оси трубопроводов при значениях h1 и h2. Принять плотности жидкостей: воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3; бензина ρбенз = 720 кг/м3.
Купить задачу 1.8а
Задача 1.9а,в
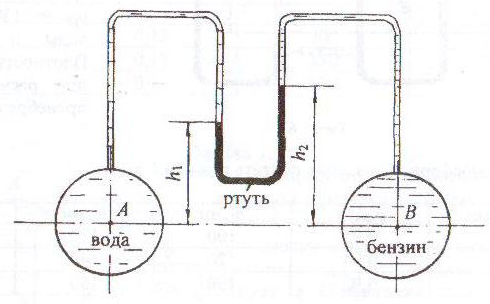
С помощью дифференциального ртутного манометра контролируется разность давлений на уровне оси трубопровода А (pA) и оси трубопровода В (pB), заполненных водой (рис. 1.9).
Определить показание ртутного манометра hрт, если известна разность давлений по оси трубопроводов – (pB – pA). Ось трубопровода В выше оси трубопровода А на величину h. Принять плотности жидкостей: воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.9а
Купить задачу 1.9в
Задача 1.10а
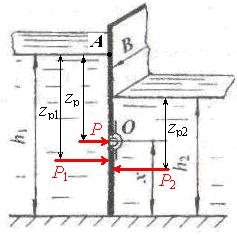
К двум трубопроводам А и В, заполненным водой и бензином, подключен U-образный ртутный манометр, показание которого hрт. На уровне оси трубопровода А установлен манометр, показание которого pман. Ось трубы В находится выше оси трубы А на расстоянии z (рис. 1.10).
Определить, какое давление, манометрическое или вакуумметрическое, показывает мановакуумметр (МВ), установленный на уровне оси труб В, если высота уровня ртути в левом колене манометра относительно оси трубы А равно h. Принять плотность жидкостей: воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3; бензина ρбенз = 720 кг/м3.
Купить задачу 1.10а
Задача 1.11а
Два трубопровода А и В, заполненные водой, соединены U-образным ртутный манометром (рис. 1.11).
Определить показание ртутного манометра hрт, если показание манометра М на уровне оси трубопровода А – pман, показание мановакуумметра (МВ) на уровне оси трубопровода В соответствует вакууму pвак. Ось трубы А выше оси трубы В на величину Z. Высота уровня ртути от оси В равна h.
Принять плотность ртути ρрт = 13,6 · 103 кг/м3; воды ρ = 103 кг/м3.
Купить задачу 1.11а
Задача 1.12а
Цилиндрический резервуар А соединен трубопроводом с водонапорным баком В (рис. 1.12). Для контроля уровня воды в баке и действующего напора установлен пьезометр на высоте Н от подводящего трубопровода.
1. Определить показания манометра М (рман в ат), установленного на трубопроводе, если пьезометрическая высота hp.
2. Определить показание U-образного ртутного манометра hpт, установленного на высоте h от оси трубы. Принять тоже показание пьезометра hp, понижение уровня ртути в левом канале а, плотность воды ρ = 103 кг/м3, ртути ρ = 13,6 · 103 кг/м3.
Купить задачу 1.12а
Задача 1.13а
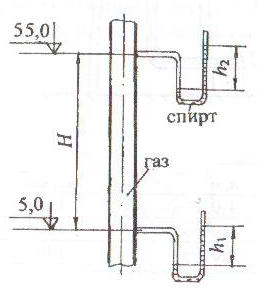
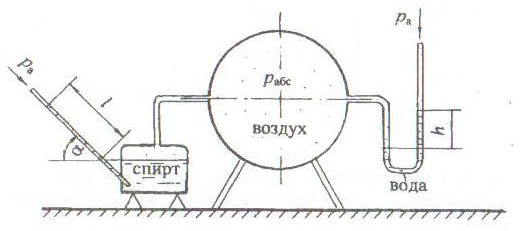
В газовом трубопроводе на отметке 5,0 м давление снимается с помощью U-образной трубки, заполненной спиртом, показание которой h1 (рис. 1.13). Определить показание U-образного манометра h2 на высоте Н, считая плотность воздуха и газа неизменными по высоте трубопровода.
При расчете учесть плотности: газа ρгаз; воздуха ρвозд; спирта ρсп.
Купить задачу 1.13а
Задача 1.14а
Открытый напорный бак А, служащий для подачи воды лабораторным установкам при постоянном напоре Н, соединен трубопроводом с цилиндрическим резервуаром В. Постоянство напора Н контролируется по показанию чашечного ртутного манометра hрт, установленного на расстоянии h от оси трубы (рис.1.14). Определить поправку а чашечного манометра.
Принять плотность воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.14а
Задача 1.15в
Определить показание манометра (рман в ат), установленного по центру трубопровода с маслом, если показание U-образного ртутного манометра hрт, высота столба воды над ртутью h (рис. 1.15).
Уровень ртути в левом колене находится на высоте Z от оси трубы.
Принять плотности жидкостей: масла ρмасл = 900 кг/м3; воды ρ = 103 кг/м3; ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.15в
Задача 1.16б
Для определения давления в воздуховоде установлена U-образная трубка, заполненная водой. Для большей точности замеров в случае необходимости подключается чашечный микроманометр с наклонной трубкой, заполненной спиртом (рис. 1.16).
Определить абсолютное давление (рабс) в воздуховоде по показанию U-образного манометра h, а также рассчитать показание микроманометра (l в мм), если угол наклона трубки. Принять атмосферное давление (ра) в мм рт. ст. Плотности жидкостей: спирта ρсп = 790 кг/м3; воды ρ = 103 кг/м3. Плотность воздуха в расчетах можно не учитывать.
Купить задачу 1.16б
Задача 1.17а
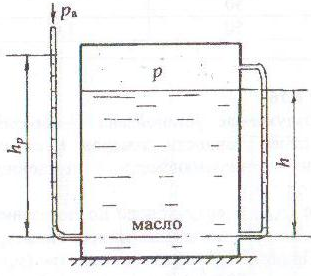
В закрытом резервуаре масло находится под давлением. Для измерения уровня масла в резервуаре справа выведен уровнемер в виде стеклянной трубки, слева на том же уровне установлен пьезометр для измерения давления в резервуаре (рис. 1.17).
Рассчитать абсолютное давление на поверхности масла (р = рабс) при показаниях уровнемера h и пьезометра hр.
Считать атмосферное давление (ра) в мм рт. ст., плотность масла ρмасл = 900 кг/м3.
Купить задачу 1.17а
Задача 1.18в
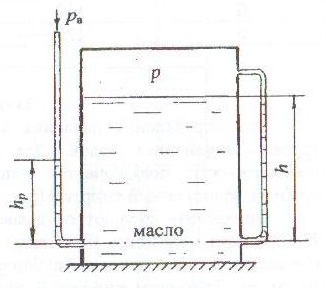
В закрытом резервуаре, заполненном маслом, на поверхности масла действует давление р. Справа в резервуаре установлена стеклянная трубка в виде уровнемера, показание которой h, слева на том же уровне выведена пьезометрическая трубка для измерения давления (рис. 1.18).
Определить показание пьезометра hр, если на поверхности масла создан вакуум (р = рвак). В расчетах учесть атмосферное давление (ра) в мм рт. ст., высоту столба масла в уровнемере (h) в метрах.
Принять плотность масла ρмасл = 900 кг/м3.
Купить задачу 1.18в
Задача 1.19а,в
В закрытом баке, заполненном бензином, установлено три прибора для регистрации давления: пружинный манометр, учитывающий давление на поверхности бензина, U-образный манометр, заполненный ртутью и водой, и пьезометр, выведенный у дна резервуара (рис. 1.19).
В установке предусмотрен уровнемер в виде закрытой стеклянной трубки для отсчета значений H, h, a.
Определить показание манометра (рман в ат) и высоту уровня бензина в пьезометре hр, если высота столба воды hв, показание U-образного ртутного манометра hрт.
В расчетах учесть высоты уровней бензина H, h, a (см. рис. 1.19). Принять плотности жидкостей: воды ρ = 103 кг/м3; бензина ρбенз = 720 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.19а
Задача 1.20а
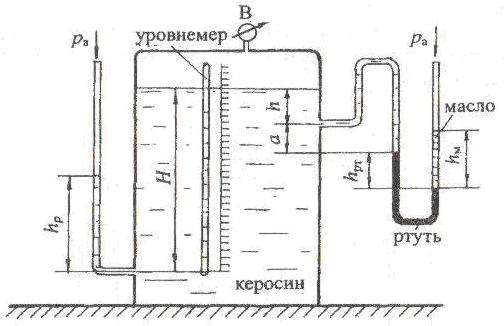
В закрытом резервуаре на поверхности керосина поддерживается вакуумметрическое давление. В зависимости от точности измерения и производственной необходимости давление на определенном уровне можно определить по пьезометру, выведенному у дна, и U-образному манометру, заполненному ртутью и маслом (рис. 1.20).
Определить показание вакуумметра В (рвак в ат) и U-образной трубки hрт, если глубина заполнения по уровнемеру H; показание пьезометра hр; высота столба масла над ртутью hм; высоты уровней керосина h и a (см. рис. 1.20).
Принять плотности жидкостей: керосина ρкер = 800 кг/м3; масла ρмасл = 900 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.20а
Задача 1.21а,в
Определить, каким прибором следует измерять давление на глубине h в баке, заполненном маслом (рис. 1.21), а также показание этого прибора (в ат), если показание U-образного ртутного манометра, установленного на поверхности масла, hрт.
Принять плотности жидкостей: масла ρмасл = 900 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.21а
Задача 1.22а
Определить показание U-образного ртутного манометра hрт, подключенного на глубине h к закрытому резервуару с маслом, если показание пружинного манометра, установленного на глубине h1, равно pман (рис. 1.22).
Понижение уровня ртути в левом колене манометра равно а.
Принять плотности жидкостей:
масла ρмасл = 900 кг/м3;
ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.22а
Задача 1.23а,б
Два резервуара А и В, линии центров которых совпадают, соединены двухколенным ртутным манометром. Резервуар А заполнен водой, резервуар В – воздухом (рис 1.23).
Определить давление воздуха рх в резервуаре B, если показание манометра по центру резервуара А – рман, а разности уровней ртути в дифференциальном манометре равны h1 и h2. Уровень ртути в левом колене расположен ниже оси в резервуаре A на величину h. Пространство между уровнями ртути в жидкостном манометре заполнено маслом плотностью ρмасл = 880 кг/м3. Принять плотность ртути ρрт = 13,6 · 103 кг/м3; плотность воды ρ = 103 кг/м3. Плотностью воздуха при расчётах можно пренебречь.
Купить задачу 1.23а
Купить задачу 1.23б
Задача 1.25а
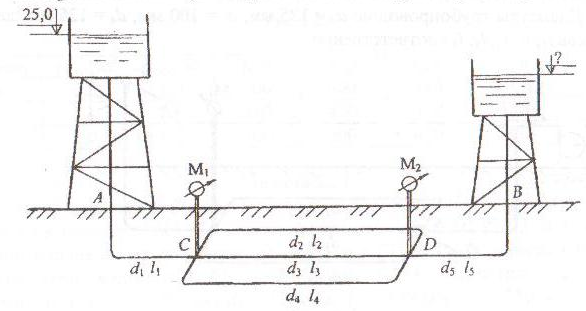
Два резервуара А и В, заполненные водой и бензином, линии центров которых находятся на одном уровне, соединены двухколенным ртутным манометром (рис. 1.25). Пространство между уровнями ртути в манометре заполнено маслом плотностью ρмасл = 900 кг/м3.
Определить, в каком резервуаре на уровне оси давление больше и на какую величину, если высоты уровней жидкостей соответственно равны h1,h2, h3,h4.
Принять плотность бензина ρбенз = 720 кг/м3; ртути ρрт = 13,6 · 103 кг/м3; воды ρ = 103 кг/м3.
Купить задачу 1.25а
Задача 1.27б
Определить разность давлений (в ат) в центрах трубопроводов А и В, заполненных водой и маслом, если высоты уровней воды и масла в U-образном ртутном дифференциальном манометре соответственно hв и hм (рис. 1.27). Принять плотности жидкостей: масла ρмасл = 900 кг/м3, ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.27б
Задача 1.29б,в
В закрытом резервуаре, заполненном маслом, на свободной поверхности действует избыточное давление ризб (рис 1.29).
Для определения величины этого давления к резервуару подключен двухколенный ртутный манометр. Рассчитать избыточное давление (ризб) в атмосферах по показанию U-образных трубок, если высоты уровней жидкостей соответственно равны h; h1; h2; h3 (см. рис 1.29).
Принять плотности жидкостей: масла ρмасл = 900 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.29в
Задача 1.30в
Из открытого резервуара C через трубу B вода поднята в резервуар A с глубиной заполнения h (рис. 1.30). Давление воздуха на поверхности воды в резервуаре A измерено U-образным ртутным манометром, показание которого hрт.
Определить глубину заполнения (h) в резервуаре А, если высота трубы В равна H. Принять плотность воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 1.30в
Задача 1.32в
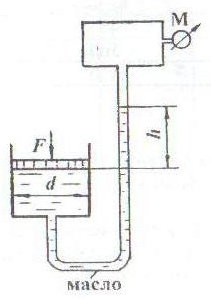
К поршню гидроцилиндра диаметром d в центре приложена вертикальная сила F (рис. 1.32). В трубке, соединяющей гидроцилиндр с воздушным резервуаром, турбинное масло поднялось на высоту h.
Определить показание манометра, установленного на воздушном резервуаре, при котором поршень находится в равновесном состоянии. Вес поршня в расчетах не учитывать. Плотность масла ρмасл = 900 кг/м3.
Купить задачу 1.32в
Задача 1.33б
Два трубопровода А и В транспортируют бензин. Центры трубопроводов находятся на одной линии (рис. 1.33).
По центру трубопроводов выведен дифференциальный пьезометр, заполненный водой. Кран прибора закрыт.
Определить, в каком трубопроводе на уровне центра давление бензина больше (pА или pВ) и на какую величину Δp. Высоты уровней бензина в пьезометрах hА и hВ.
Принять плотность воды ρ = 103 кг/м3; бензина ρбенз = 720 кг/м3.
Купить задачу 1.33б
Задача 2.1б
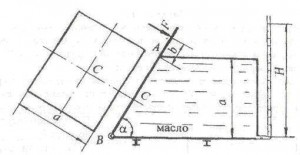
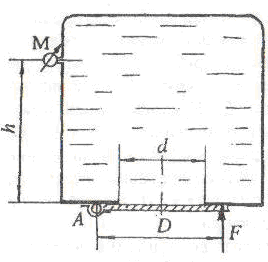
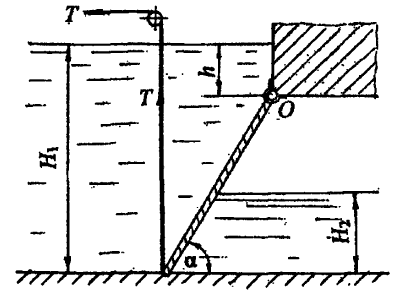
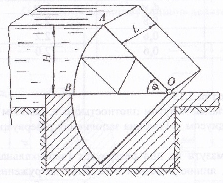
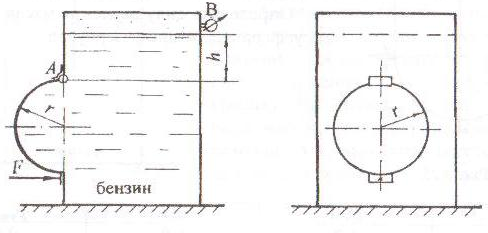
Поворотный клапан АО закрывает выход из бензобака в трубу квадратного сечения со стороной a. Клапан опирается на срез трубы, сделанный под углом α = 45°. С другой стороны клапана – воздух (рис. 2.1).
Определить силу натяжения троса T, необходимую для открытия клапана, если уровень бензина над нижней кромкой клапана H, давление на поверхности бензина соответствует показанию манометра pман. Плотность бензина ρбенз = 700 кг/м3. Трение в шарнирной опоре О и в ролике В не учитывать.
Купить задачу 2.1б
Задача 2.2а
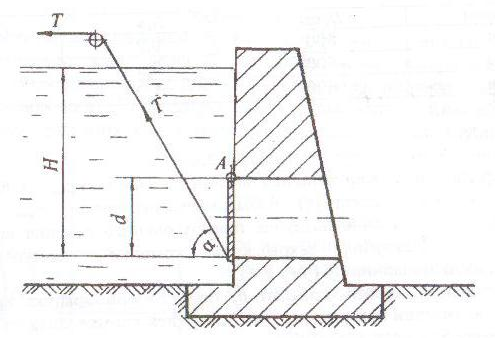
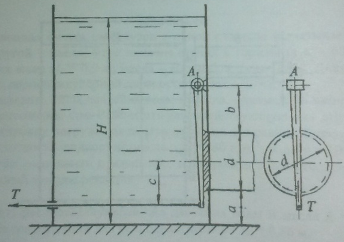
В плотине сделано водопропускное отверстие в виде трубы диаметром d. Труба перекрывается круглым затвором, имеющим неподвижную горизонтальную ось вращения, проходящую через точку А (рис. 2.2).
Определить силу натяжения троса (Т), необходимую для открытия затвора. Трос прикреплен к нижней кромке крышки под углом α к горизонту. Глубина воды над нижней кромкой затвора Н. Массу затвора не учитывать.
Купить задачу 2.2а
Задача 2.3а
Закрытый резервуар, заполненный маслом плотностью ρмасл = 900 кг/м3, имеет выпускную трубу диаметром D, перекрытую дисковым затвором с осью поворота, проходящей горизонтально через точку О (рис. 2.3). На поверхности масла действует манометрическое давление рман. Уровень масла над нижней кромкой трубы. Определить равнодействующую давления на дисковый затвор и момент этой силы относительно оси поворота затвора.
Купить задачу 2.3а
Задача 2.4а
Закрытый резервуар заполнен маслом плотностью ρмасл = 900 кг/м3. На поверхности масла действует избыточное давление рман. Выход из резервуара сделан в виде патрубка прямоугольного сечения высотой h и шириной b. Патрубок закрывается крышкой, поворачивающейся относительно оси шарнира А (рис. 2.4).
Определить ширину крышки b, при которой крышка находится в закрытом положении при условии, что к верхней кромке крышки приложена заданная сила F.
Принять высоту крышки h, глубину масла над верхней кромкой крышки а.
Купить задачу 2.4а
Задача 2.5а
Поворотный вертикальный затвор квадратного сечения со стороной а, перекрывающий вход воды в штольню, может вращаться вокруг горизонтальной оси шарнира О, проходящей через центр затвора (рис. 2.5).
Определить силу F, которую нужно приложить к нижней кромке затвора, чтобы удержать его в заданном положении, если глубина воды перед затвором h. В штольне справа – воздух. Трением в шарнире О пренебречь.
Представить аналитический и графо-аналитический методы определения величины силы давления воды, её линии действия и точки приложения.
Плотность воды ρ = 103 кг/м3.
Купить задачу 2.5а
Задача 2.7а
Вход в туннель перекрыт прямоугольным деревянным щитом, который удерживается в вертикальном положении двумя тросами (рис. 2.7). Ширина щита B, толщина досок δ. Глубина воды над верхней кромкой щита h. Щит удерживает напор воды слева h1, глубина воды в туннеле h2. Рассчитать аналитическим и графоаналитическим методами силы давления воды на щит слева и справа, глубины центров давления для этих сил, показать линии действия этих сил.
Определить равнодействующую давления, а также подъемное усилие (Т) двух тросов. Коэффициент трения в направляющих пазах f = 0,5. Принять плотность дерева ρдер = 1,2 · 103 кг/м3, воды ρ = 103 кг/м3.
Купить задачу 2.7а
Задача 2.8а
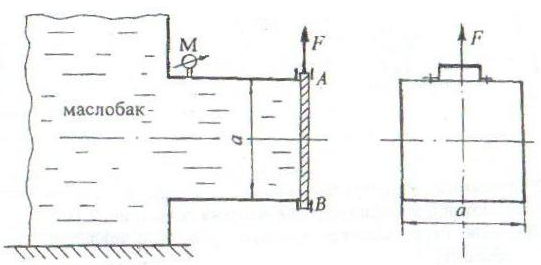
Патрубок маслобака квадратного сечения со стороной а перекрывается крышкой АВ, перемещающейся в вертикальных пазах (рис. 2.8).
Определить начальную силу F для открытия крышки, если показание манометра, установленного на верхней стенке патрубка, рман.
Принять плотность масла ρмас = 900 кг/м3, коэффициент трения скольжения в пазах f = 0,5.
Массу крышки считать равной М.
Купить задачу 2.8а
Задача 2.9а
В закрытом резервуаре, заполненном водой, выведен внутренний патрубок прямоугольного сечения высотой h и шириной b для выпуска воды. Патрубок перекрыт крышкой АВ, расположенной под углом α = 60° к горизонту, шарнирно укреплённой на оси А. (рис. 2.9).
Открытие крышки для выпуска воды осуществляется за счет создания вакуума на поверхности воды.
Определить наименьшее вакуумметрическое давление на поверхности воды (pвак) для открытия крышки, если глубина воды на уровне нижней кромки крышки H. Масса крышки М.
Купить задачу 2.9а
Задача 2.10а
В открытом резервуаре, заполненном водой, сделан внутренний патрубок высотой h и шириной b для выпуска воды (рис. 2.10).
Патрубок перекрывается крышкой АВ, установленной под углом α = 60° к горизонту.
Определить силу натяжения вертикального троса (T) для открытия крышки при глубине заполнения H. Крышка может поворачиваться относительно шарнира А. Масса крышки М.
Представить аналитический и графо-аналитический методы расчета силы давления воды. Трением в шарнире и ролике пренебречь.
Купить задачу 2.10а
Задача 2.11а,б
В закрытом резервуаре, заполненном бензином, выведен патрубок квадратного сечения со стороной h для выпуска бензина (рис. 2.11). Патрубок перекрыт крышкой АВ, установленной под углом α = 60°. Крышка поворачивается шарнирно относительно оси А.
Определить нормальное усилие (Т) в точке В для удержания крышки в закрытом положении, если действующий напор на уровне нижней кромки крышки H. Давление на поверхности бензина соответствует показанию U-образного ртутного манометра hрт.
Принять жидкостей: бензина ρбенз = 720 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Массу крышки не учитывать.
Купить задачу 2.11а
Задача 2.12а
Определить нормальное усилие F, приложенное к наклонной крышке АВ для удержания крышки в закрытом положении (рис. 2.12). Крышка расположена под углом α = 60° к горизонту, укреплена с помощью шарнира В и перекрывает патрубок квадратного сечения со стороной а. Патрубок заполнен маслом плотностью ρмасл = 900 кг/м3.
К дну патрубка присоединен пьезометр, показание которого H. Сила F приложена по нормали к крышке на расстоянии b от стенки патрубка. Силу тяжести крышки не учитывать.
Решение представить аналитическим и графо-аналитическим методами.
Купить задачу 2.12а
Задача 2.13а
Выход из резервуара, заполненного водой, представляет патрубок, который закрывается круглой крышкой диаметром D. Крышка может поворачиваться вокруг шарнира A (рис. 2.13).
Определить силу T для удержания крышки в закрытом положении, если показание U-образного ртутного манометра hрт, высота уровня масла над ртутью hм. Уровень ртути в правом колене манометра выше шарнира А на величину а.
Принять плотности жидкостей: ртути ρрт = 13,6 · 103 кг/м3; масла ρмасл = 900 кг/м3.
Купить задачу 2.13а
Задача 2.14а
Патрубок закрытого резервуара с маслом перекрывается круглой крышкой, которая может поворачиваться вокруг шарнира А (рис 2.14).
Определить, каким должно быть показание U-образной трубки, заполненной ртутью (hрт), определяющей давление на поверхности масла, чтобы крышка находилась в закрытом положении за счёт вакуума.
Принять: диаметр крышки D, глубину масла до шарнира A равной h. Плотность масла ρмасл = 900 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 2.14а
Задача 2.15в
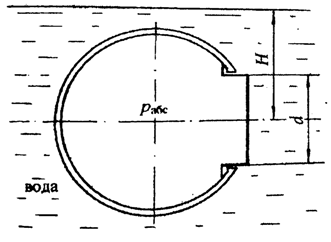
Сферический резервуар, плавающий в воде, имеет люк, закрытый изнутри плоской вертикальной круглой крышкой диаметром d (рис. 2.15).
Определить горизонтальную равнодействующую давления на крышку, линию действия силы и ее положение, если абсолютное давление внутри резервуара pабс, уровень воды над осью крышки H.
Найти расстояние еравн от линии действия равнодействующей до оси крышки.
Плотность воды ρ = 103 кг/м3.
Купить задачу 2.15в
Задача 2.17а,б
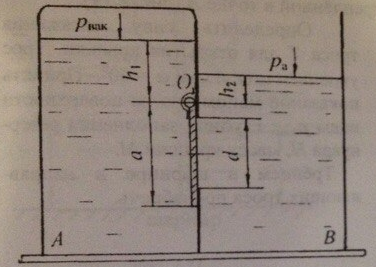
В вертикальной перегородке отстойника, состоящего из двух резервуаров – А и В (рис. 2.17), сделано круглое отверстие диаметром d. Отверстие перекрывается квадратное крышкой со стороной а, которая может поворачиваться вокруг шарнира О.
Определить, какой вакуум (pвак) нужно создать на поверхности воды в закрытом резервуаре А, чтобы крышка открылась. Резервуар В открыт. Принять уровень воды над шарниром О в резервуаре А равным h1, в резервуаре В – h2.
Купить задачу 2.17а
Купить задачу 2.17б
Задача 2.18а,б
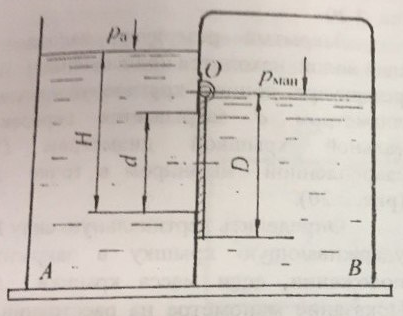
Отстойник для воды, представляющий два резервуара – А и В, разделен вертикальной перегородкой, в которой сделано круглое отверстие диаметром d (рис. 2.18). Отверстие закрывается круглой крышкой диаметром D. Крышка может поворачиваться относительно шарнира О. Напор воды в резервуаре А на уровне нижней кромки крышки равен Н. Вода в резервуаре В находится на уровне шарнира.
Определить величину манометрического давления pман на поверхности воды в резервуаре В для удержания крышки в закрытом положении.
Купить задачу 2.18а
Купить задачу 2.18б
Задача 2.19а
В закрытом резервуаре с водой круглое донное отверстие закрывается крышкой диаметром D, шарнирно укрепленной в точке А (рис. 2.19).
Определить силу натяжения троса Т для открытия крышки. Трос укреплен под углом α = 60°. Принять показание манометра на поверхности воды рман; глубину заполнения резервуара Н; массу крышки М.
Трением в шарнире и направляющих троса пренебречь.
Купить задачу 2.19а
Задача 2.20а
Закрытый резервуар, заполненный водой, находится под давлением. В резервуаре донное круглое отверстие диаметром d закрывается горизонтальной крышкой диаметром D, закрепленной шарниром в точке А (рис. 2.20).
Определить вертикальную силу F, удерживающую крышку в закрытом положении, если масса крышки М. Показание манометра на расстоянии h от дна равно рман.
Купить задачу 2.20а
Задача 2.21а
Прямоугольный плоский щит, перекрывающий канал шириной В, вверху поддерживается двумя крюками, расположенными симметрично, а внизу соединен шарнирно с дном канала (рис. 2.21).
Слева щит удерживает напор воды h1, справа – h2. Крюки укреплены на расстоянии а от верхнего уровня воды. Определить реакции крюков Rкр от действия воды на щит.
Купить задачу 2.21а
Задача 2.22а,б
Определить величину и линию действия силы давления нефти на перегородку в цилиндрическом баке диаметром d, если показание вакуумметра pвак, показание манометраpман (рис. 2.22). Найти расстояние eравн от линии действия равнодействующей сил давления до оси цилиндрического бака. Принять плотность нефти ρнеф = 800 кг/м3.
Купить задачу 2.22а
Купить задачу 2.22б
Задача 2.23а,в
Промывочный колодец для удаления загрязненной воды имеет отводную трубу диаметром d, перекрываемую плоским круглым клапаном. Периодическое открытие клапана производится с помощью троса, прикрепленного к шарнирному устройству с осью в точке А (рис. 2.23).
Определить силу натяжения троса T, необходимую для открытия клапана, при глубине заполнения колодца H. Нижняя кромка отверстия находится на расстоянии a от дна, верхняя кромка – на расстоянии b от шарнира. Трос укреплен на расстоянии с от оси клапана. Принять плотность загрязненной воды ρ = 1050 кг/м3.
Купить задачу 2.23а
Купить задачу 2.23в
Задача 2.24б
Квадратное отверстие со стороной а в вертикальной плоской стенке закрытого резервуара с водой перекрывается плоским щитом при помощи устройства с шарниром А (рис. 2.24). Щит прижимается к стенке грузом G на расстоянии b от шарнира А.
Найти величину силы G тяжести для удержания щита в закрытом положении, если глубина воды на уровне нижней кромки отверстия Н. Верхняя кромка отверстия находится на расстоянии h от шарнира А. Абсолютное давление на поверхности воды pабс.
Купить задачу 2.24б
Задача 2.25а
Водопроводная труба диаметром d имеет поворот под углом α = 90° (рис. 2.25). Манометрическое давление в трубеpман.
Определить равнодействующую давления на упор.
Примечание: следует рассчитать силы давления в симметрично расположенных фланцевых соединениях А и В, затем равнодействующую этих сил.
Купить задачу 2.25а
Задача 2.26в
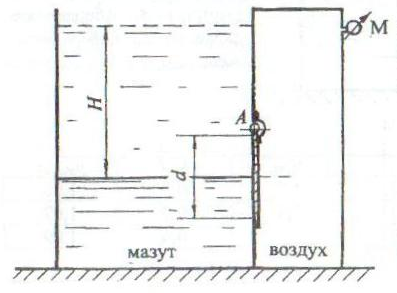
Открытый резервуар, заполненный мазутом, имеет перегородку с круглым отверстием диаметром d. Отверстие закрывается круглой крышкой, укрепленной с помощью шарнира А (рис. 2.26). Справа от перегородки закрытый воздушный резервуар. Давлением воздуха регулируется открытие крышки для выпуска мазута.
Определить величину манометрического давления в резервуаре с воздухом pман, чтобы крышка была в закрытом положении:
1) если уровень мазута доходит до центра крышки;
2) если уровень мазута над осью крышки равен H.
Принять плотность мазута ρмаз = 920 кг/м3.
Купить задачу 2.26в
Задача 2.27в
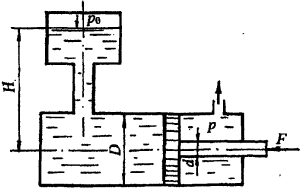
Определить давление р в правой части гидроцилиндра диаметром D, заполненного маслом «Индустриальное 20» (рис. 2.27).
Сила, действующая на шток діаметром d при равновесном состоянии поршня, равна F.
Принять избыточное давление на поверхности масла р0, напор масла на уровне оси поршня Н, плотность масла ρмасл = 890 кг/м3.
Купить задачу 2.27в
Задача 2.28б
Определить силу F на штоке золотника (рис. 2.28), если действующий напор в подводящей системе H, показание вакуумметра (В) равно pвак. Избыточное давление в полости поршней pизб, диаметры поршней соответственно D и d. Система заполнена водой плотностью ρ = 103 кг/м3.
Купить задачу 2.28б
Задача 2.29в
Определить нагрузку на болты крышек AB и CD гидравлического цилиндра диаметром D, если к плунжеру диаметром d приложена сила F (рис. 2.29).
Купить задачу 2.29в
Задача 2.33б,в
Определить вертикальную силу F на рычажном механизме, необходимую для удержания поршня на высоте h1 над поверхностью воды в колодце, над поршнем поднимается столб воды высотой h2 (рис. 2.33).
Диаметр поршня равен D, штока – d. Рычажный механизм имеет шарнирную опору в точке А. Длины рычагов механизма соответственно равны а и b (см. рис. 2.33).
Вес поршня и штока не учитывать.
Плотность воды ρ = 103 кг/м3.
Купить задачу 2.33в
Задача 2.41б
Из резервуара, заполненного маслом, выведен треугольный патрубок высотой h и шириной b, который перекрывается крышкой, укрепленной вертикально с помощью шарнира А (рис. 2.41).
Плотность масла ρ = 900 кг/м3.
Определить горизонтальную силу F, необходимую для удержания треугольной крышки в закрытом положении, если показание манометра на уровне нижней кромки крышки рман.
Купить задачу 2.41б
Задача 2.42б
В отстойнике для воды разделительная стенка в виде прямоугольного щит может поворачиваться шарнирно относительно оси О (рис. 2 42).
Определить, на каком расстояние х от дна отстойника следует расположить ось шарнира О, чтобы щит шириной В открывался автоматически, если глубина воды слева превысит величину h1. Глубина воды справа равна h2. Вес щита не учитывать.
Решение представить аналитическим и графо-аналитическим методами.
Купить задачу 2.42б
Задача 2.43б
Определить усилие Т, которое нужно приложить к вертикальному тросу для открытия щита, перекрывающего канал прямоугольного сечения. Щит расположен под углом α = 60° к горизонту и закреплен шарнирно в т. О (рис. 2.43). Ширина щита в плоскости, перпендикулярной плоскости чертежа, равна В. Глубина воды перед щитом Н1, за щитом Н2. Уровень воды над шарниром h. Масса щита равной М.
Купить задачу 2.43б
Задача 2.44а
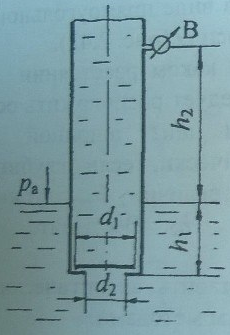
Во всасывающем трубопроводе центробежного насоса на входе установлен обратный клапан в виде диска диаметром d1, который перекрывает входное отверстие диаметром d2 для пропуска воды (рис. 2.44). Трубопровод заглублен под уровень h1.
Определить, каким должно быть показание вакуумметра В (pвак) на высоте h2 для открытия клапана в момент пуска насоса.
Атмосферное давление pа = 740 мм рт. ст.
Купить задачу 2.44а
Задача 3.3а
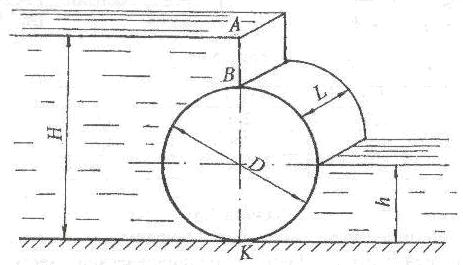
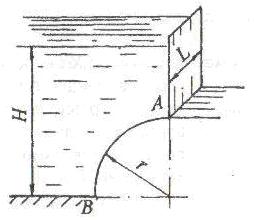
Определить численные значения, линии действия и точки приложения горизонтальной и вертикальной составляющих сил давления воды на стенку резервуара АКВ, состоящую из вертикальной плоской стенки АК и цилиндрической поверхности КВ с секторным углом 90° (рис. 3.3). Ширина резервуара В, напоры воды соответственно равны Н1 и Н2.
Показать положение равнодействующей давления, её точку приложения, а также найти угол наклона равнодействующей к горизонту.
Купить задачу 3.3а
Задача 3.4а
Определить величину равнодействующей давления воды на секторный затвор АВ (рис. 3.4), линию действия, угол наклона к горизонту и глубину центра давления hDравн.
Удерживаемый напор Н, ширина затвора В, секторный угол затвора φ.
Купить задачу 3.4а
Задача 3.5а
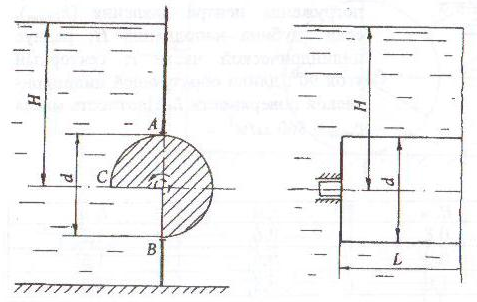
В горизонтальной цистерне диаметром D и длиной L хранится бензин. Уровень бензина в цистерне находится на высоте Н от дна. Избыточное давление паров бензина на поверхности соответствует показанию манометра рман (рис. 3.5).
Определить горизонтальные силы, действующие на боковые цилиндрические поверхности АВ цистерны. Показать линии действия сил и глубину (hD) центра давления от свободной поверхности для этих сил. Плотность бензина ρбенз = 720 кг/м3.
Купить задачу 3.5а
Задача 3.7а
Определить величину и угол наклона к горизонту равнодействующей давления воды на устройство в виде цилиндрического затвора (рис. 3.7), если диаметр цилиндра D, действующий напор слева H, cправа h = D/2. Длина цилиндрического затвора L.
Купить задачу 3.7а
Задача 3.8а
Закрытый резервуар с полуцилиндрическим дном радиусом r и длиной L заполнен маслом плотностью ρмасл = 900 кг/м3 (рис. 3.8). Сила давления масла на дно резервуара равна R. Определить, на какой высоте H от оси цилиндрической части установлен вакуумметр, показание которого рвак.
Купить задачу 3.8а
Задача 3.9а
Определить равнодействующую давления масла на цилиндрическую стенку резервуара АВ (рис. 3.9), линию действия, угол наклона силы и глубину погружения центра давления (hDравн), если глубина наполнения H; радиус цилиндрической части r, секторный угол 90°; длина образующей цилиндрической поверхности L. Плотность масла ρмасл = 860 кг/м3.
Купить задачу 3.9а
Задача 3.10а
Определить равнодействующую давления воды, её угол наклона к горизонту, и глубину погружения центра давления для цилиндрической поверхности АВ с секторным углом φ = 120° (рис. 3.10).
Длина цилиндрической поверхности L, действующий напор воды слева H, cправа h = H/2.
При решении чертёж представить в масштабе, в виде вертикального сечения криволинейной поверхности.
Купить задачу 3.10а
Задача 3.11а
В вертикальной стенке резервуара сделано прямоугольное отверстие для выпуска воды. Отверстие перекрывается цилиндрическим затвором диаметром d и длиной L, установленным на цапфах (рис. 3.11). Действующий напор на уровне оси затвора H.
Определить величину, линию действия, геометрическое положение и угол наклона к горизонту равнодействующей давления на поверхность затвора ACB.
Чертеж выполнить в масштабе.
Купить задачу 3.11а
Задача 3.12а
В прямоугольном окне вертикальной стенки резервуара, заполненного водой, установлен на цапфах цилиндрический затвор диаметром d и длиной L. Удерживаемый напор воды на уровне оси затвора H (рис. 3.12).
Определить величину, линию действия и угол наклона к горизонту равнодействующей давления воды на поверхность затвора ACB.
Чему равно усилие на каждую цапфу.
Чертеж выполнить в масштабе.
Купить задачу 3.12а
Задача 3.13а
Закрытый резервуар, заполненный мазутом плотностью ρ = 920 кг/м3, имеет полуцилиндрическое дно радиусом r. Глубина заполнения резервуара H, длина резервуара L (рис. 3.13).
Определить силу давления мазута на дно резервуара (вертикальная сила давления), а также величину, линию действия и глубину погружения центра давления hD от свободной поверхности для сил давления на боковые поверхности АВ (горизонтальная сила давления).
Принять абсолютное давление на поверхности мазута рабс.
Купить задачу 3.13а
Задача 3.14а,б
Определить величину равнодействующей давления воды на секторный затвор АВ шлюзной камеры (рис. 3.14), а также линию действия силы, угол наклона к горизонту и глубину центра давления для силы hD.
Щит поворачивается относительно оси О и при открытии заходит в углубление – нишу флютбета.
Длина шлюзной камеры L, удерживаемый напор Н, угол раствора щита φ.
При решении чертеж представить в масштабе, щит в виде сечения вертикальной плоскостью.
Принять плотность воды ρ = 103 кг/м3.
Купить задачу 3.14а
Купить задачу 3.14б
Задача 3.17а
Определить силу давления воды на дно цилиндрической поверхности цистерны AKB, показать ее линию действия, а также разрывающие усилия, действующие на боковые поверхности цистерны AK и BK, показать линию действия сил и глубину hD точек приложения сил от свободной поверхности (рис. 3.17).
Цистерна диаметром D, длиной L наполовину заполнена водой. На поверхности воды действует избыточное давление pман, соответствующее показанию манометра. Плотность воды ρ = 103 кг/м3.
Купить задачу 3.17а
Задача 3.18а
Определить силу давления воды на верхнюю и нижнюю половины сферического резервуара радиусом r, полностью заполненного водой, а также растягивающее усилие в болтах фланцевого соединения (6 болтов), если показание манометра, установленного под углом α в нижней части резервуара равно pман (рис. 3.18).
Купить задачу 3.18а
Задача 3.19а
Определить равнодействующую давления воды на цилиндрическую поверхность АВ закрытого резервуара (рис. 3.19), если секторный угол цилиндрической поверхности равен 90°, показать линию действия силы, рассчитать угол наклона силы к горизонту и глубину погружения центра давления hD для равнодействующей.
Принять: радиус цилиндрической поверхности r, длину поверхности L, глубину заполнения резервуара Н, абсолютное давление на поверхности воды рабс, плотность воды ρ = 103 кг/м3.
Чертеж представить в масштабе.
Купить задачу 3.19а
Задача 3.20а
Определить силу давления бензина на полусферическое дно цилиндрического резервуара радиусом r (рис. 3.20), если показание манометра, установленного на расстоянии h от дна резервуара, равно pман. Принять плотность бензина ρбенз = 720 кг/м3.
Купить задачу 3.20а
Задача 3.21а
Определить величину, линию действия, угол наклона и глубину центра давления равнодействующей hDравн на полусферическую крышку в плоской вертикальной стенке закрытого резервуара (рис. 3.21), заполненного бензином.
Принять: радиус полусферы r, показание пьезометра, выведенного на уровне нижней кромки крышки Н, плотность бензина ρбенз.
Купить задачу 3.21а
Задача 3.22а
В резервуаре, заполненном бензином, в вертикальной плоской стенке круглое отверстие диаметром d закрыто конусной крышкой длиной l (рис. 3.22).
Определить горизонтальную и вертикальную силы давления бензина на конусную крышку. Показать их линии действия и геометрическое положение, а также положение равнодействующей сил.
Уровень бензина над верхней кромкой крышки h. Показание мановакуумметра (МВ) соответствует манометрическому давлению pман.
Плотность бензина ρбенз = 750 кг/м3.
Масса конической крышки М.
Купить задачу 3.22а
Задача 3.23а
В закрытом резервуаре, заполненном бензином, в боковой плоской стенке сделано круглое отверстие, которое закрывается полусферической крышкой радиусом r (рис. 3.23). Крышка укреплена с помощью шарнира в точке А. На расстоянии h от шарнира на свободной поверхности бензина действует вакуумметрическое давление pвак.
Определить усилие F для удержания крышки в закрытом положении. Принять плотность бензина ρбенз = 720 кг/м3.
Купить задачу 3.23а
Задача 3.25а
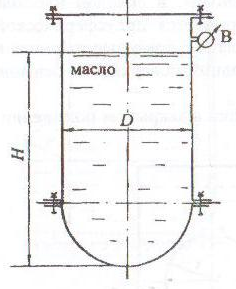
Закрытый цилиндрический резервуар диаметром D с полусферическим дном заполнен трансформаторным маслом плотностью ρмас = 880 кг/м3 (3.25).
Глубина заполнения резервуара равна H. На поверхности масла действует вакуумметрическое давление pвак.
Определить силу давления масла на полусферическое дно резервуара.
Купить задачу 3.25а
Задача 3.27б
Цилиндрический резервуар диаметром D, заполненный бензином плотность ρбенз = 750 кг/м3, закрыт полусферической крышкой, закреплённой шестью болтами (рис. 3.17). Резервуар находится под давлением. Показание манометра на глубине h от оси крышки равно pман.
Определить величину и направление растягивающей силы, воспринимаемой болтами, соответствующей вертикальной силе давления на полусферическую крышку. Рассчитать горизонтальные силы, разрывающие полусферическую крышку по сечению 1–1, показать расстояние линий действия этих сил от оси полусферы.
Купить задачу 3.27б
Задача 3.33б
В боковой плоской стенке закрытого резервуара, заполненного маслом, круглое отверстие закрыто полусферической крышкой ACB радиусом r. На высоте Н от оси полусферы установлен манометр, показание которого pман (рис. 3.33).
Определить величину равнодействующей давления масла на крышку, линию действия ее, угол наклона силы к горизонту и глубину точки приложения силы. Плотность масла ρмасл = 900 кг/м3.
Чертеж представить в масштабе.
Купить задачу 3.33б
Задача 4.2в
В закрытом резервуаре с избыточным давлением на поверхности масла, соответствующим показанию манометра pман, трансформаторное масло подается в открытый отстойник по трубе диаметром d и длиной l (рис. 4.2). На трубе установлен пробковый кран с углом закрытия α.
Определить, какой должна быть разность уровней масла в баке и отстойнике (H) для обеспечения пропускной способности трубопровода Q.
Принять плотность масла ρмасл = 884 кг/м3; коэффициент кинематической вязкости масла νмасл = 30 · 10-6 м2/с
Купить задачу 4.2в
Задача 4.3а,в
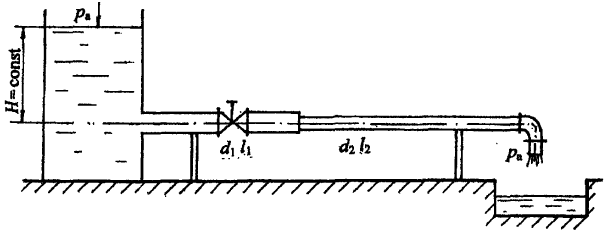
Определить расход воды Q из дозаторного резервуара A в резервуар B (рис. 4.3) при постоянном напоре H по двум трубам диаметром и длиной: d1, l1 и d2, l2 соответственно.
Трубы водопроводные нормальные. На середине трубы диаметром d2 установлен пробковый кран с углом закрытия α.
Учесть потери напора в местных сопротивлениях на входе и выходе трубопроводной системы, а также при внезапном расширении трубопровода. Построить напорную и пьезометрическую линии, показать эпюру потерь напора.
Купить задачу 4.3а
Задача 4.4а
Из закрытого резервуара с избыточным давлением на поверхности рман вода подаётся в открытый резервуар на высоту Н (рис. 4.4). Для определения расхода воды на магистральном трубопроводе диаметром d1 = 100 мм и длиной l установлен расходомер Вентури с диаметром цилиндрической вставки d2 = 50 мм. Разность показаний пьезометров расходомера h.
Определить пропускную способность системы Q и высоту подъёма воды H. Считать трубы водопроводные в нормальных условиях.
Учесть потери напора во всех местных сопротивлениях, принимая коэффициент сопротивления вентиля ζвент. Потерями напора в расходомере можно пренебречь.
Купить задачу 4.4а
Задача 4.5а,б,в
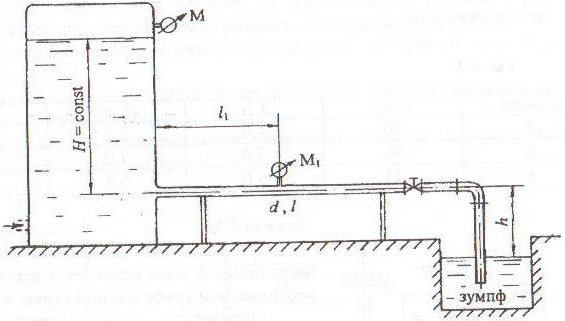
Из бака с постоянным напором вода подается в зумпф, уровень воды в котором также постоянный и ниже оси трубы на величину h (рис. 4.5).
Определить напор воды H в баке, чтобы расход воды, пропускаемый по трубопроводу диаметром d и длиной l, был равен Q.
Труба водопроводная, чугунная с абсолютной шероховатостью Δ. В системе установлен пробковый кран с углом закрытия α.
Плотность воды ρ = 103 кг/м3; коэффициент кинематической вязкости воды ν = 1 · 10-6 м2/с.
Купить задачу 4.5а
Купить задачу 4.5б
Купить задачу 4.5в
Задача 4.6б
При постоянном напоре вода по двум трубам подается из резервуара А в резервуар В (рис. 4.6).
Определить разность уровней воды в резервуарах H при расходе Q. Диаметры и длины труб соответственно: d1, l1 и d2, l2, абсолютная шероховатость труб: Δ1 = Δ2 = 0,5 мм. На трубе диаметром d1 на расстоянии (1/3)l1 от входа в трубу установлен вентиль с коэффициентом сопротивления равным ζвент.
Учесть потери напора в местных сопротивлениях: на входе и выходе трубопровода, а также при внезапном расширении.
Принять коэффициент кинематической вязкости воды ν = 1 · 10-6 м2/с.
Построить напорную и пьезометрическую линии, показать эпюру потерь напора.
Купить задачу 4.6б
Задача 4.7а,в
Из резервуара А в резервуар В вода подается по трубопроводу диаметром d = 50 мм с абсолютной шероховатостью Δ = 0,5 мм, состоящему из трех участков соответственно длиной: l1, l2 и l3 (рис. 4.7).
Расход воды в системе Q. На входе в трубу установлена решетка без обратного клапана, на первом участке стоит вентиль с коэффициентом сопротивления ζвент. Напор воды в резервуаре А – Н1, в резервуаре В – Н2.
Определить показание манометра pман2 на поверхности воды в резервуаре В, если показание манометра на поверхности воды в резервуаре А pман1. Кинематический коэффициент вязкости воды ν = 1 · 10-6 м2/с.
Построить напорную и пьезометрическую линии, показать эпюру потерь напора.
Купить задачу 4.7а
Задача 4.8а
Из напорного бака с постоянным напором H вода подается в зумпф по двум трубам диаметрами и длиной d1, l1 и d2, l2 соответственно (рис. 4.8).
Определить расход воды в трубопроводе и скорости движения воды в каждой трубе. На трубе диаметром d1 установлен пробковый кран с углом закрытия α. Учесть потери напора на входе в трубу с острыми кромками, а также при внезапном сужении ζв.с, а также в колене на выходе. Трубы водопроводные нормальные.
Купить задачу 4.8а
Задача 4.9а
С помощью насоса вода подается в напорный бак на высоту Н, по трубе диаметром d, длиной l (рис.4.9). Показание манометров: в начале трубопровода pман1, в конце – pман2.
Определить, при каком коэффициенте сопротивления пробкового крана ζкр будет обеспечен расход Q.
Абсолютная шероховатость трубы Δ; коэффициент кинематической вязкости воды ν = 1 · 10-6 м2/с.
Купить задачу 4.9а
Задача 4.10а
При закрытом кране на трубопроводе диаметром d и длиной l показание манометра перед краном pман (рис. 4.10).
Определить показание манометра при открытом кране, если слив воды происходит в мерную ёмкость. За время t наполняется объем W.
Труба водопроводная с абсолютной шероховатостью Δ. Учесть потери напора на входе в трубу с острыми кромками. Принять коэффициент кинематической вязкости воды ν = 1 · 10-6 м2/с.
Купить задачу 4.10а
Задача 4.11а
На водопроводной трубе диаметром d = 50 мм установлены три местных сопротивления: вентиль, диафрагма и пробковый кран. Расход воды постоянный (Q = const). Слив воды производится в мерную емкость (рис. 4.11).
Определить среднюю скорость движения воды в трубе V и расход Q. Рассчитать коэффициенты местных сопротивлений всех устройств, кроме этого, для пробкового крана угол закрытия α (см. приложение, табл. 4).
Разности показаний пьезометров: у вентиля hв; диафрагмы hд; крана hкр. В мерной емкости объем W наполняется за время t.
Взаимное влияние местных сопротивлений и потери напора по длине трубы не учитывать.
Купить задачу 4.11а
Задача 4.12а
Определить показание U-образного спиртового манометра hсп, установленного на трубе Вентури в вентиляционном трубопроводе при значении диаметров d1 и d2, если расход воздуха Q. Принять плотность воздуха ρвозд = 1,23 кг/м3; плотность спирта ρсп = 820 кг/м3. Коэффициент сопротивления трубы Вентури принять равным ζвент (рис. 4.12).
Купить задачу 4.12а
Задача 4.13а
Для измерения расхода воды в трубопроводе диаметром d1 установлен расходомер Вентури с диаметром цилиндрической части d2 (рис. 4.13). К широкой и узкой части расходомера подсоединены пьезометры в виде U-образной трубки, расстояние между которыми равно z.
Пренебрегая потерями напора в расходомере, определить скорости в широкой и узкой частях трубы Вентури, а также расход воды Q в трубопроводе, если разность показаний пьезометров h. При расчете давлением воздуха в пьезометре пренебречь. Коэффициент Кориолиса принять равным единице (α = 1,0).
Купить задачу 4.13а
Задача 4.14а,в
Для определения расхода воздуха в пневмотранспортной системе на входе в воздуховод установлен входной коллектор с плавным входом (рис. 4.14).
Определить расход воздуха Q в воздуховоде диаметром d, если показание чашечного микроманометра, заполненного спиртом, lсп, учесть синус угла наклона трубки микроманометра (sinα).
Коэффициент сопротивления на входе в коллектор – ζвх.
Принять плотности: воздуха ρвозд = 1,25 кг/м3; спирта ρсп = 890 кг/м3.
Купить задачу 4.14а
Задача 4.16б,в
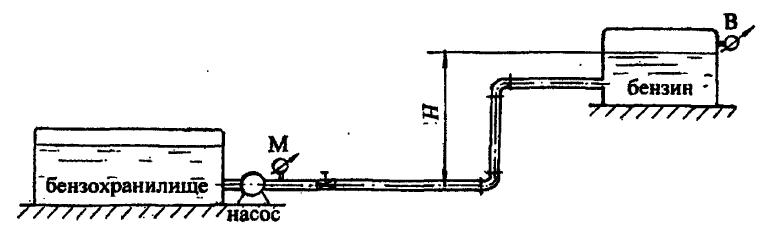
Бензин из бензохранилища с помощью насоса подается в бензобак на высоту H. На поверхности бензина в бензобаке поддерживается вакуум рвак (рис. 4.16).
Определить, каким должно быть манометрическое давление (рман в ат) на выходе из насоса при подаче Q, если транспортирование бензина происходит по стальной трубе длиной l, диаметром d с абсолютной шероховатостью Δ, на трубе установлена задвижка Лудло со степенью закрытия a/d, учесть потери напора в двух коленах и на выходе из трубы в бензобак.
Принять плотность бензина ρбенз = 720 кг/м3; коэффициент кинематической вязкости бензина νбенз = 0,65 · 10-6 м2/с.
Купить задачу 4.16б
Купить задачу 4.16в
Задача 4.17а,в
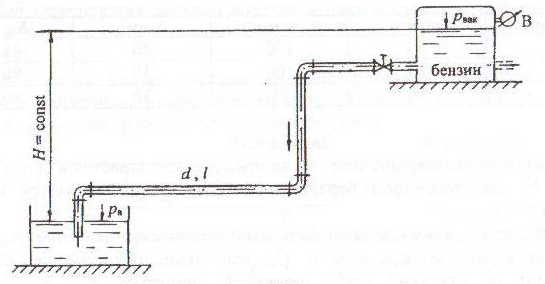
Из напорного бака по стальной трубе длиной l, диаметром d с абсолютной шероховатостью Δ бензин подается в открытый резервуар (рис. 4.17). Транспортирование производится при постоянном напоре Н. На поверхности бензина в баке действует вакуумметрическое давление pвак. Пропускная способность системы Q. На трубопроводе установлен вентиль с коэффициентом сопротивления ζвент.
Определить величину вакуума (pвак) в бензобаке. Принять плотность бензина ρбенз = 750 кг/м3; коэффициент кинематической вязкости бензина νбенз = 0,9 · 10-6 м2/с.
Купить задачу 4.17а
Купить задачу 4.17в
Задача 4.18а
Определить, на какой высоте h следует установить шестеренчатый насос системы смазки, подающий масло «Турбинное 22» при расходе Q по стальной трубе диаметром d и длиной l. Показание вакуумметра на входе в насос pвак (рис. 4.18).
В системе установлен пробковый кран с углом закрытия α. Учесть потери напора в двух коленах при коэффициенте сопротивления ζкол и на входе в трубу из маслобака ζвх. Принять плотность масла ρмасл = 900 кг/м3, коэффициент кинематической вязкости νмасл = 22 · 10-6 м2/с.
Купить задачу 4.18а
Задача 4.19а
Определить предельную длину трубопровода диаметром d с абсолютной шероховатостью Δ, с помощью которого бензин может быть поднят на высоту Н при пропускной способности Q, если показание манометра после насоса рман (рис 4.19). Истечение бензина происходит под уровень. Учесть потери напора в пробковом кране при угле закрытия α, трех коленах и на выходе из трубы в резервуар больших размеров.
Принять плотность бензина ρбенз = 720 кг/м3, коэффициент кинематической вязкости бензина νбенз = 0,65 · 10-6 м2/с.
Купить задачу 4.19а
Задача 4.20а,б,в
Бензин из бензохранилища с помощью насоса подается в закрытый бензобак на высоту H. Показание манометра, установленного после насоса, рман (рис 4.20).
Определить показание мановакуумметра (рм.в. в ат), измеряющего давление на поверхности бензина в бензобаке, если расход бензина Q.
Транспортирование бензина производится по новой стальной трубе длиной l, диаметром d с абсолютной шероховатостью Δ. На трубе установлен пробковый кран с углом закрытия α. Учесть потери напора в трех коленах и на выходе из трубы в бензобак.
Принять плотность бензина ρбенз = 720 кг/м3; коэффициент кинематической вязкости бензина νбенз = 0,65 · 10-6 м2/с.
Купить задачу 4.20а
Задача 4.21а
Из закрытого резервуара с избыточным давлением на поверхности (pман) вода истекает в атмосферу по двум трубам диаметрами и длиной d1, l1 и d2, l2 соответственно. Трубы чугунные с эквивалентной шероховатостью Δ1 = Δ2 = 1,35 мм. Действующий напор воды постоянный H (рис. 4.21).
Определить показание манометра pман при пропускной способности Q. Учесть потери напора в местных сопротивлениях: на входе в трубу, при внезапном сужении с коэффициентом сопротивления ζв.с; в пробковом кране с углом закрытия α, установленном на середине второй трубы. Коэффициент кинематической вязкости воды ν = 1 · 10-6 м2/с.
Построить напорную, пьезометрическую линии, эпюру потерь напора.
Купить задачу 4.21а
Задача 4.22а
Из закрытого резервуара по двум трубам диаметрами d1 и d2 и длиной l1 и l2 вода истекает в атмосферу (рис. 4.22). Движение воды происходит при постоянном напоре H. На расстоянии l1/3 от входа в первую трубу установлена задвижка Лудло со степенью открытия a/d.
Определить расход воды Q в системе, принимая трубы водопроводные в нормальных условиях. Учесть потери напора на входе в первую трубу, в задвижке Лудло, а также при внезапном расширении.
Построить напорную и пьезометрическую линии, показать эпюру потерь напора.
Купить задачу 4.22а
Задача 4.23а,б
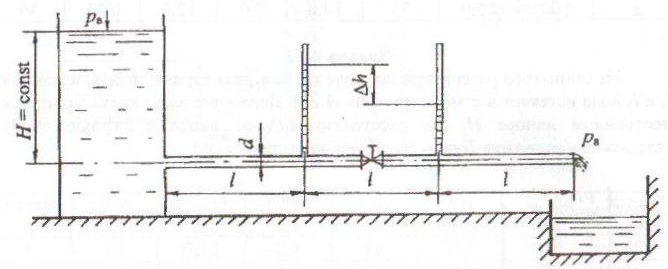
Вода из напорного бака с постоянным напором (H = const) по горизонтальной трубе диаметром d вытекает в атмосферу (рис. 4.23). Труба водопроводная нормальная состоит из трех участков длиной l каждый. Участки разделены пьезометрами, разность показаний которых Δh.
На середине второго участка установлен пробковый кран с углом закрытия α.
Определить действующий напор H и расход воды Q. Потерями напора при входе в трубу пренебречь.
Построить пьезометрическую линию и линию полного напора, показать эпюру потерь напора.
Купить задачу 4.23а
Купить задачу 4.23б
Задача 4.25а,в
Из открытого резервуара с глубиной наполнения h вода истекает в атмосферу по вертикальной трубе длиной l (рис. 4.25).
Определить диаметр трубы d для пропуска расхода Q. Уровень воды в резервуаре постоянный, скоростным напором на поверхности воды в резервуаре пренебречь. Считать трубу водопроводной в нормальных условиях.
Методические указания: задача решается методом подбора диаметров: принимаются диаметры по ГОСТу, например, d1 = 100 мм; d2 = 75 мм; d3 = 50 мм, рассчитывается действующий напор H = h + l, сравнивается с заданным значением и выбирается наиболее приемлемый вариант.
Купить задачу 4.25а
Задача 4.26в
Из напорного бака с избыточным давлением на поверхности pман вода подается в зумпф по нормальной водопроводной трубе диаметром d, длиной l (рис. 4.26). На расстоянии l1 показание манометра равно pман1. В системе установлен пробковый кран с углом закрытия α. Потерями напора при входе в трубу пренебречь. Уровень воды в зумпфе ниже оси трубы на величину h.
Определить напор воды в баке H и расход Q.
Купить задачу 4.26в
Задача 4.27б
Истечение воды в атмосферу происходит по горизонтальной трубе диаметром d, длиной l при постоянном напоре в резервуаре H (рис. 4.27). На расстоянии l/3 от входа в трубу установлен пьезометр, показание которого h.
Определить расход воды Q, л/с, и коэффициент гидравлического сопротивления λ. Потерями на входе в трубу пренебречь.
Построить пьезометрическую линию и линию полного напора, показать эпюру потерь напора.
Купить задачу 4.27б
Задача 4.29б
С помощью насоса вода подается на высоту H с истечением в атмосферу по водопроводной трубе в нормальных условиях (рис. 4.29).
Диаметр трубы d, длина трубы l, пропускная способность системы Q. В системе установлена задвижка Лудло со степенью закрытия a/d. Трубопровод имеет два колена с углом поворота α = 90° и одно колено с углом поворота α1 = 60°, для которого коэффициент сопротивления ζкол = 0,7.
Определить показание манометра М (pман), установленного после насоса, а также показание мановакуумметра МВ (pм.в), установленного в верхней точке трубопровода на высоте h от выхода из трубопровода.
Купить задачу 4.29б
Задача 4.33б
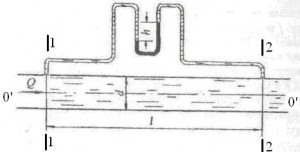
На горизонтальном трубопроводе на расстоянии l выведен U-образный дифференциальный пьезометр, заполненный ртутью для определения потерь напора по длине hl (рис. 4.33). Разность уровней ртути в U-образной трубке h; диаметр трубопровода d; расход воды Q.
Определить коэффициент Дарси λ, вычислить гидравлический уклон I. Плотность жидкостей: воды ρ = 103 кг/м3; ртути ρрт = 13,6 · 103 кг/м3.
Купить задачу 4.33б
Задача 5.1а
Из водонапорной башни А с отметкой уровня горизонта воды 20,0 м вода подается потребителям В и С с расходами QВ и QС по трубам диаметром и длиной d1, l1 и d2, l2 соответственно (рис. 5.1).
Определить отметки в пунктах В и С, на уровне которых будут обеспечены заданные расходы. Построить пьезометрическую линию, показать эпюру потерь напора. Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять равными 5 % от потерь по длине.
Купить задачу 5.1а
Задача 5.3а
Водонапорная башня А с отметкой 22,0 м питает два потребителя – В и С – через систему двух последовательно соединённых труб (рис. 5.3). Пьезометрический напор в конце первого участка равен hp.
Определить расход воды на первом участке Q1 и расход потребителя С(QC), а также отметку потребителя С. Принять расход потребителя Вравным QB.
Диаметры и длины участков водопроводной системы соответственно равны d1,l1 и d2, l2. Трубы водопроводные нормальные. Местные потери напора принять равными 5 % от потерь по длине. Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.3а
Задача 5.4а,б
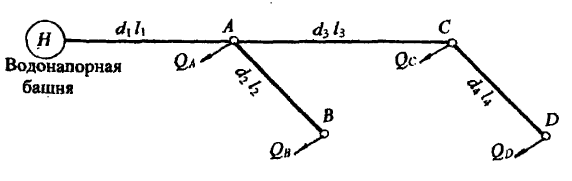
Из водонапорного бака А с избыточным давлением на поверхности рман по трём последовательно соединённым трубам вода подаётся потребителям В, С и D с одинаковыми расходами: QB = QC = QD = Q. У потребителя D – выход воды в атмосферу (рис. 5.4).
Определить расход воды на каждом участке трубы, диаметры и длины участков соответственно равны d1, l1; d2, l2; d3, l3. Действующий напор считать постоянным, равным H. Трубы водопроводные нормальные. Местные потери принять равными 10% от потерь по длине. Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.4а
Купить задачу 5.4б
Задача 5.5а,в
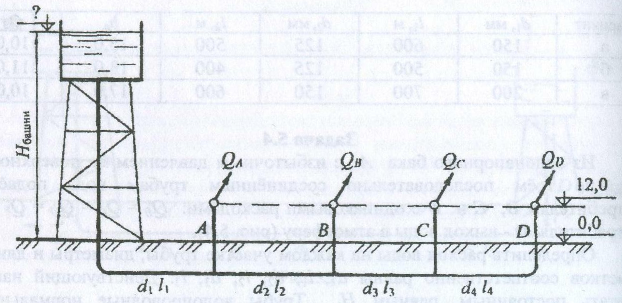
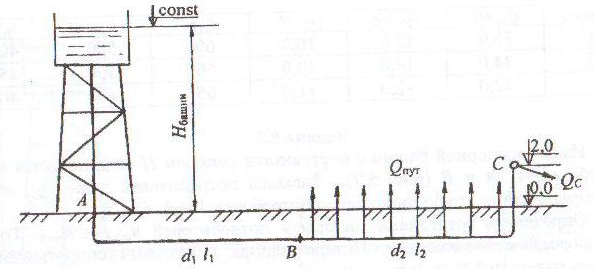
Из водонапорной башни по трубопроводам вода поступает четырём потребителям – А, В, С и D – на отметку 12,0 м. Расходы потребителей составляют соответственно QA; QB; QC и QD (рис. 5.5).
Определить отметку уровня воды в водонапорной башне (Hбаш), считая её постоянной. Построить пьезометрическую линию и эпюру потерь напора, показать отметки пьезометрических напоров в узловых точках A, В и С. Диаметры участков труб принять: d1 = 200 мм; d2 = 200 мм; d3= 150 мм; d4= 125 мм; длины участков – соответственно l1, l2, l3, l4. Потери напора в местных сопротивлениях принять равными 5 % от потерь по длине.
Купить задачу 5.5а
Купить задачу 5.5в
Задача 5.6б,в
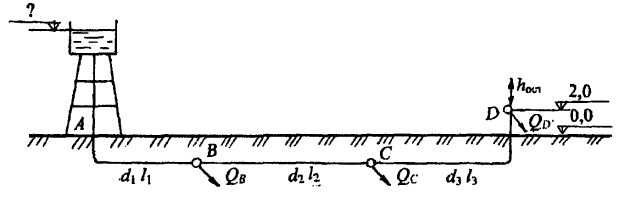
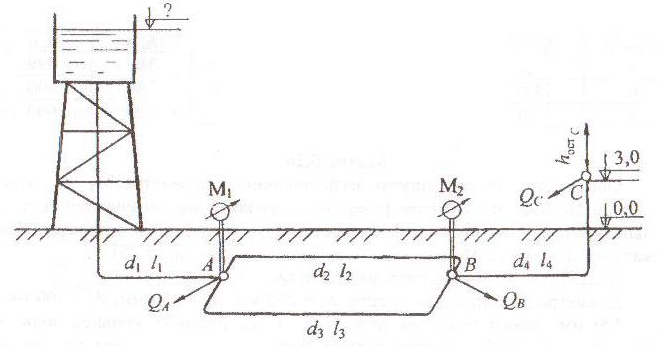
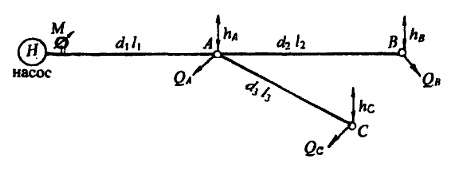
Из водонапорной башни А обеспечивается водой три потребителя в точках В, С и D. Пропускная способность первого участка Q1; расходы потребителей: QB и QC (рис. 5.6).
Определить расход потребителя D (QD, л/с), а также отметку свободной поверхности воды в водонапорной башне, если остаточный напор у потребителя D (hост.D) должен быть не менее 10 м. Принять диаметры участков труб: d1 = 200 мм, d2 = 150 мм, d3 = 125 мм; длины участков – l1, l2 и l3.
Трубы водопроводные нормальные, местные сопротивления составляют 10% от потерь по длине. Построить пьезометрическую линию, показать эпюру потерь напора.
Купить задачу 5.6б
Купить задачу 5.6в
Задача 5.7а
Из водонапорной башни с постоянным напором H вода подается двум потребителям А и В (рис. 5.7). Расходы потребителей равны QА и QВ; диаметры и длины трубопроводов до потребителей – d1, l1 и d2, l2.
Определить остаточные напоры у потребителей hостА и hостВ. Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять 5 % от потерь по длине.
Купить задачу 5.7а
Задача 5.8а
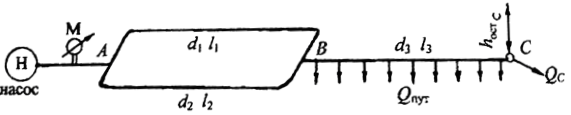
Из водонапорной башни А вода поступает потребителю C с расходом QС на отметку 2,0 м (рис. 5.8). Водопроводная система состоит из двух участков. Диаметры и длины участков соответственно равны d1, l1 и d2, l2. На втором участке предусмотрен путевой расход Qпут.
Определить действующий напор водонапорной башни Hбашн при постоянной отметке горизонта воды.
Построить пьезометрическую линию и эпюру потерь напора. Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять равными 5 % от потерь по длине.
Купить задачу 5.8а
Задача 5.9а
От насосной установки по двум трубам диаметрами и длиной соответственно d1, l1 и d2, l2, вода подаётся двум потребителям – А и В – с расходами QА и QВ. На втором участке предусмотрена равномерная раздача воды с путевым расходом Qпут (рис. 5.9).
Определить остаточные напоры у потребителей А и В, если показание манометра, установленного после насоса, равно pман.
Трубы водопроводные нормальные. Местные сопротивления принять равными 10% от потерь по длине. Построить пьезометрическую линию.
Купить задачу 5.9а
Задача 5.10а
Из напорного бака с постоянным уровнем вода подаётся в нижележащие горизонты рудника трём потребителям – А, В и С – с расходами QА, QВ и QС по системе трёх последовательно соединенных труб длиной l1, l2 и l3 соответственно (рис. 5.10). Остаточный напор у потребителя С должен быть не менее 10 м (hост ≥ 10,0 м)
Подобрать диаметры труб на каждом участке при условии, чтобы эксплуатационная скорость не превышала 1,2 м/с (Vэксп ≤ 1,2 м/с).
Определить, на какой высоте H должен быть расположен уровень воды в напорном баке. Трубы водопроводные нормальные, потери напора в местных сопротивлениях принять равными 5 % от потерь по длине.
Купить задачу 5.10а
Задача 5.11а
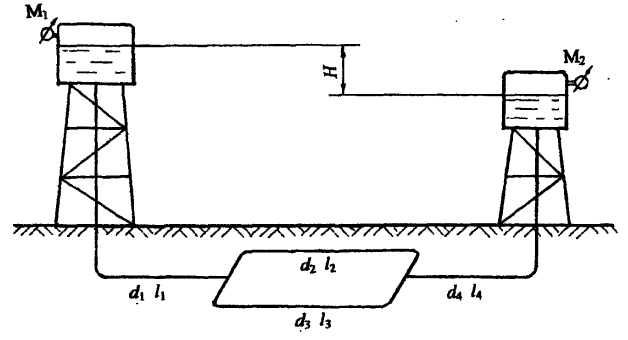
Из двух напорных резервуаров A и C – вода подается потребителю В в количестве QВ = Q1 + Q2 (рис. 5.11). Диаметры и длины участков сети соответственно равны d1, l1 и d2, l2.
Определить отметки горизонтов воды в резервуарах A и C, если напор воды у потребителя В равен HВ. Трубы водопроводные нормальные. Местные потери напора принять равными 5 % от потерь по длине.
Построить пьезометрическую линию, показать эпюру потерь напора.
Купить задачу 5.11а
Задача 5.12а
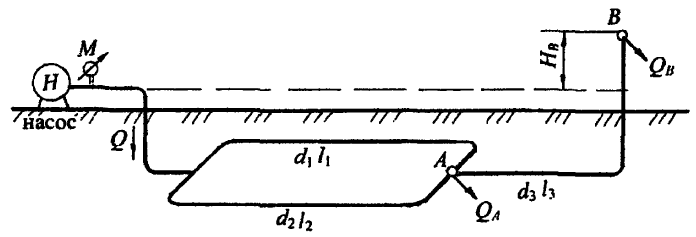
От насосной установки вода подаётся двум потребителям – А и В – с расходами QА и QВ соответственно (рис. 5.12).
У потребителя В вода подается на высоту 12,0 м.
Определить показание манометра М (pман) после насоса и манометра М1 (pман1) на середине второго участка системы. Диаметры и длины участков труб соответственно равны d1, l1 и d2, l2.
Трубы водопроводные нормальные. Местные потери принять равными 5 % от потерь напора по длине. В вертикальной плоскости чертежа построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.12а
Задача 5.13а
Из напорного бака А вода подается двум потребителям – В и C на отметку 3,0 м, расходы потребителей QВ и QС (рис. 5.13). Диаметры и длины труб соответственно равны d1, l1 и d2, l2. На первом трубопроводе предусмотрена непрерывная раздача воды в виде путевого расхода Qпут.
Определить отметку уровня воды в напорном баке А. Трубы водопроводные нормальные, потери напора в местных сопротивлениях принять равными 10 % от потерь напора по длине.
Купить задачу 5.13а
Задача 5.14а,б,в
Из водонапорного бака А, в котором давление на поверхности соответствует показанию манометра pман, вода подается потребителям В и С с расходами QВ и QС по двум последовательно соединенным трубам диаметрами и длиной d1, l1 и d2, l2 соответственно (рис. 5.14).
Определить возможный остаточный напор у потребителя С (hост), если действующий напор равен H. Трубы водопроводные нормальные, потери напора в местных сопротивлениях принять равными 5 % от потерь напора по длине. Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.14а
Купить задачу 5.14б
Купить задачу 5.14в
Задача 5.15в
От насосной установки вода подается потребителю В. Для обеспечения бесперебойной подачи воды в систему включены три параллельно проложенные трубопровода диаметрами d1 = 200 мм, d2 = 150 мм, d3 = 200 мм, соответственно длинами l1, l2 и l3, четвертый магистральный участок диаметром d4 = 250 мм, длиной l4 (рис. 5.15).
Показание манометра, установленного после насоса, равно pман. Остаточный напор у потребителя В должен быть не менее 8 м (hост ≥ 8,0 м).
Определить возможный расход у потребителя В (QВ), а также пропускную способность параллельных труб (Q1, Q2 и Q3).
Трубы водопроводные нормальные. Потери напора на магистральном участке до точки А разветвления труб и в местных сопротивлениях принять равными 15 % от потерь по длине.
В вертикальной плоскости чертежа построить пьезометрическую линию, показать эпюру потерь напора.
Купить задачу 5.15в
Задача 5.17а,б
Из водонапорного бака А вода по системе труб поступает потребителю D. Отметка горизонта воды в баке постоянная, равная 18,0 м. На участке BC трубы закольцованы (рис. 5.17). Диаметры участков сети: d1 = 150 мм, d2 = 125 мм, d3 = 200 мм, длины участков l1, l2, l3. Трубы водопроводные нормальные. Расход воды на втором участке равен Q2.
Определить расходы воды на третьем участке (Q3 = QD) и остаточный напор у потребителя D (hостD). Потери напора на участке AB не учитывать. Местные потери напора принять равными 5 % от потерь по длине.
Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.17б
Задача 5.18а
От насосной установки по трубопроводной системе с параллельным соединением труб вода подается двум потребителям – А и В – с расходами QА и QВ (рис. 5.18). Диаметры участков системы: d1 = 100 мм, d2 = 125 мм, d3 = 125 мм; длины участков соответственно l1, l2, l3.
Высота подъема воды у потребителя В относительно магистрального трубопровода HВ.
Определить распределение расходов в параллельных участках труб Q1 и Q2, а также показание манометра, установленного после насоса pман. Местные сопротивления принять равными 5% от потерь по длине. Потери напора на участке от насоса до узла разветвления труб не учитывать. Трубы водопроводные нормальные уложены на одном горизонте.
Построить пьезометрическую линию и эпюру потерь напора в вертикальной плоскости чертежа.
Купить задачу 5.18а
Задача 5.19а
Из центральной водонапорной башни с постоянным напором Н снабжаются три потребителя – А, В и С с расходами: QА, QВ и QС (рис. 5.19). Система включает параллельное соединение труб на участке АВ. Диаметры участков трубопроводов в системе: d1 = 250 мм, d2 = 200 мм, d3 = 150 мм, d4 = 200 мм, длины участков соответственно l1, l2, l3, l4.
Трубы водопроводные нормальные проложены на одном горизонте.
Определить расходы воды в параллельных участках Q2 и Q3, а также действующий напор Н при условии, что остаточный напор у потребителя С должен быть не менее 10 м (hост ≥ 10,0 м). Потери напора в местных сопротивлениях принять равными 10 % от потерь напора по длине. Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.19а
Задача 5.20а,б
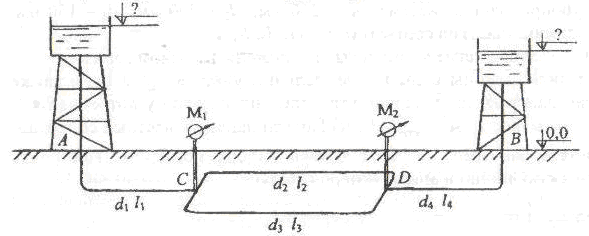
Из центральной водонапорной башни A через систему трубопроводов вода поступает в напорный бак В. На участке CD трубопроводы закольцованы (рис. 5.20). Показание первого манометра в узле разветвления C равно pман1, второго в узле D – pман2.
Диаметры участков трубопроводов: d1 = 200 мм, d2 = 150 мм, d3 = 125 мм, d4 = 150 мм; длины участков: l1, l2, l3, l4. Трубы водопроводные нормальные проложены на одном горизонте. Расход воды в системе Q.
Определить расходы воды в параллельных участках Q2 и Q3, а также отметки горизонта воды в башне A и баке В. Потери напора в местных сопротивлениях принять равными 10 % от потерь напора по длине. Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.20а
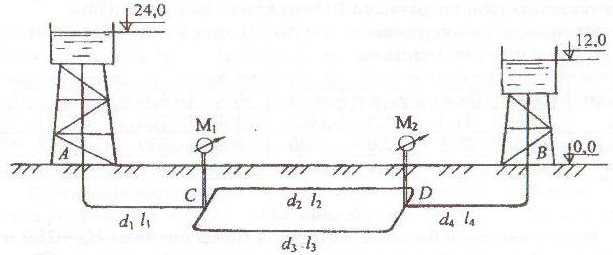
Задача 5.21а
Из водонапорной башни A с отметкой горизонта воды HА = 24,0 м вода подается в напорный бак В с отметкой горизонта воды HВ = 12,0 м. Система трубопроводов имеет закольцованный участок CD. В узлах разветвления C и D выведены манометра М1 и М2 (рис. 5.21). Диаметры участков трубопроводов d1 = 200 мм, d2 = 150 мм, d3 = 125 мм, d4 = 150 мм; длины участков: l1, l2, l3, l4 соответственно.
Трубы проложены на одном горизонте.
Определить расход воды в системе Q, а также распределение расхода в параллельных участках Q2 и Q3. Рассчитать показания манометра М1 (pман1) и манометра М2 (pман2). Трубы водопроводные нормальные. Потери напора в местных сопротивлениях составляют 10 % от потерь напора по длине.
Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.21а
Задача 5.22а
От насосной установки вода поступает двум потребителям – А и С – с расходами QА и QС. Система трубопроводов уложена на одном горизонте и включает параллельное соединение труб на участке АВ (рис. 5.22). В узле В выведен манометр М1, показание которого pман1.
Диаметры трубопроводов: d2 = 125 мм,d3 = 100 мм; d4 = 125 мм, длины участков l1, l2, l3, l4, l5 соответственно.
Рассчитать диаметры труб на первом и пятом участках системы d1 и d5 при условии, что эксплуатационная скорость в трубах Vэксп ≤ 1,2 м/с.
Определить высоту подъема воды у потребителя С (НС) и показание манометра М (pман), установленного после насоса.
Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять равными 10 % от потерь по длине.
Построить пьезометрическую линию и показать эпюру потерь напора в вертикальной плоскости чертежа.
Купить задачу 5.22а
Задача 5.23а,б
Из водонапорной башни A с отметкой горизонта воды HА = 25,0 м по системе труб, включающей кольцевое соединение на участке CD, вода подается в напорный бак В. В узлах разветвления труб выведены манометры М1 и М2 (рис. 5.23). Общий расход воды в системе равен Q.
Диаметры трубопроводов: d1 = 200 мм, d2 = 125 мм, d3 = 100 мм, d4 = 125 мм, d5 = 150 мм; длины участков: l1, l2, l3, l4, l5 соответственно.
Трубы проложены на одном горизонте.
Определить расход воды в параллельных участках кольцевого соединения Q2, Q3, Q4, показания первого и второго манометров pман1 и pман2, а также отметку горизонта воды в баке В (HВ).
Трубы водопроводные нормальные. Потери напора в местных сопротивлениях составляют 10 % от потерь напора по длине.
Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.23а
Купить задачу 5.23б
Задача 5.24в
Три потребителя – A, B и C – снабжаются водой из водонапорной башни по системе труб, уложенных на одном горизонте. Потребителю A отводится расход QА; потребителю B – QВ. На участке между потребителями A и B трубы закольцованы, в узлах отвода воды выведены манометры М1 и М2 (рис. 5.24). Показание второго манометра pман2.
Диаметры и длины участков трубопроводов: d1 = 250 мм, d2 = 200 мм, d3 = 150 мм, d4 = 150 мм, длины участков l1, l2, l3, l4 соответсвенно.
Определить расходы воды, поступающей от водонапорной башни Q = Q1, расход потребителя С (QС), показание первого манометра pман1, а также отметку горизонта воды в напорной башне.
Отметка потребителя С равна 3,0 м, остаточный напор у потребителя С hостС ≥ 10,0 м.
Трубы водопроводные нормальные, Потери напора в местных сопротивлениях принять равными 10 % от потерь напора по длине.
Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.24в
Задача 5.25а
По трубопроводной системе, представленной в плане на рис. 5.25, от насосной установки вода подается потребителю С в количестве QС. На участке АВ две трубы диаметрами d1 = 150 мм и d2 = 125 мм проложены параллельно. На участке ВС диаметром d3 = 200 мм предусмотрена равномерная раздача воды Qпут. Длины участков трубопроводов l1, l2, l3 соответственно.
Показание манометра после насоса равно pман.
Определить распределение расхода в параллельных трубах Q1 и Q2, а также возможный остаточный напор у потребителя С (hостС). Потери напора на магистральном участке от насоса до точки разветвления А не учитывать. Потери напора в местных сопротивлениях принять равными 10% от потерь напора по длине. Трубы нормальные водопроводные.
Построить пьезометрическую линию и эпюру потерь напора в вертикальной плоскости чертежа.
Купить задачу 5.25а
Задача 5.26а
Определить, каким должно быть показание манометра М1 (pман1) на поверхности воды в закрытом резервуаре, из которого по системе труб с кольцевым соединением вода поступает в другой закрытый резервуар при показании манометра М2 (pман2) на поверхности воды (рис. 5.26).
Общий расход воды в системе равен Q.
Диаметры водопроводной сети: d1 = 250 мм, d2 = 150 мм, d3 = 100 мм, d4 = 200 мм, длины участков сети: l1, l2, l3, l4. Разность уровней воды в резервуарах H. Трубы водопроводные нормальные на одном горизонте. Местные сопротивления принять равными 10 % от потерь по длине.
Построить пьезометрическую линию и эпюру потерь напора.
Купить задачу 5.26а
Задача 5.27б
Насос, дающий подачу Q, перекачивает воду в резервуар по трём параллельным трубам под уровень H (рис. 5.27).
Определить показание манометра М (pман) установленного на линии нагнетания, а также расходы воды в каждой трубе.
Принять диаметры параллельных участков сети: d1 = 150 мм, d2 = 100 мм, d3 = 125 мм, длины которых соответственно равны l1, l2, l3.
Трубы водопроводные нормальные уложены на одном горизонте. Местные потери составляют 10 % от потерь по длине. Потери напора на магистральном участке с расходом Q не учитывать.
Оценить, как изменится показание манометра, если один или два из параллельных трубопроводов будут отключены.
Купить задачу 5.27б
Задача 5.28в
Система водоснабжения, представленная в плане на рис. 5.28, имеет три потребителя – А, В и С. Определить расходы воды у потребителей (QА, QВ, QС в л/с), если свободные (остаточные) напоры у потребителей: hА, hВ, hС. Показание манометра, установленного после насоса, pман. Потребители расположены на одном горизонте.
Диаметры участков сети: d1 = 200 мм, d2 = 150 мм, d3 = 125 мм, длины участков соответственно равны l1, l2, l3. Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять равными 10 % от потерь по длине. Построить в аксонометрии пьезометрическую линию.
Купить задачу 5.28в
Задача 5.29б
Тупиковая система, представленная в плане, предназначена для снабжения водой четырех потребителей – А, В, С и D. Расходы потребителей: QА, QВ, QС, QD (рис. 5.29).
Рассчитать диаметры труб на каждом участке при условии, что средняя скорость в трубах не должна превышать υср = 1,2 м/с.
Определить высоту водонапорной башни H, если остаточные напоры у потребителей должны быть не менее 10 м (hост ≥ 10 м).
Длины участков сети: l1, l2, l3, l4. Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять равными 10 % от потерь по длине. Построить в аксонометрии пьезометрическую линию, показать эпюру потерь напора.
Купить задачу 5.29б
Задача 5.33б
Из водонапорной башни осуществляется питание потребителей А и В с расходами QА и QВ, на первом участке предусмотрен путевой расход Qпут воды (рис. 5.33).
Определить отметку горизонта воды в водонапорной башне, если отметка потребителя А равна 9,0 м, потребителя В – 12,0 м.
Три участка трубопроводов уложены в одном горизонте. Диаметры участков сети: d1 = 250 мм, d2 = 150 мм,d3 = 150 мм, длины участков соответственно равны l1, l2, l3.
Трубы водопроводные нормальные. Потери напора в местных сопротивлениях принять равными 10 % от потерь по длине.
Купить задачу 5.33б
Задач, которых нет, Вы можете заказать