Вода подается по чугунному трубопроводу в водоем

РИр.1

Задач, которых нет, Вы можете заказать

Партнерская программа

Задача 1

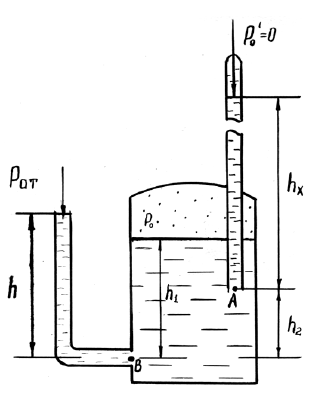
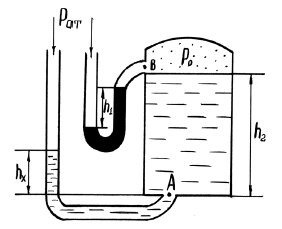
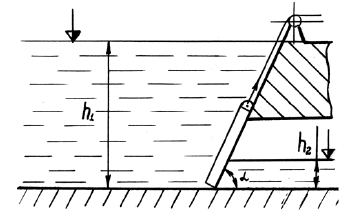
Определить приведенную пьезометрическую высоту поднятия воды h_х в закрытом пьезометре (соответствующую абсолютному гидростатическому давлению в точке А), если показание открытого пьезометра h, расстояния от точки В до свободной поверхности жидкости в резервуаре h₁, а точка А расположена выше точки В на величину h₂ (рис. 1.1). Атмосферное давление p_атм = 98,1 кПа, удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 1

Задача 2

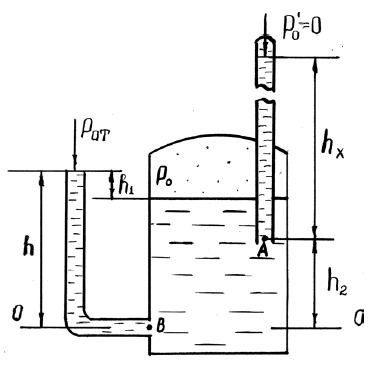
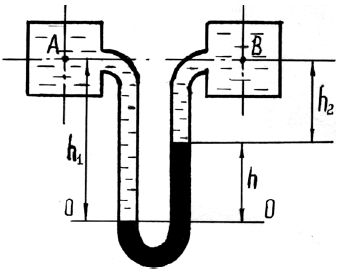
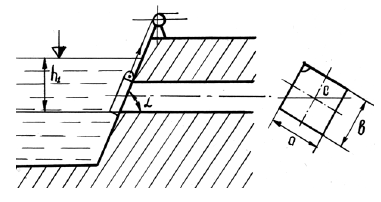
Закрытый резервуар с водой снабжен открытым и закрытым пьезометрами (рис. 1.2). Определить приведенную пьезометрическую высоту поднятия воды h_х в закрытом пьезометре (соответствующую абсолютному гидростатическому давлению в точке А), если показание открытого пьезометра h, уровень воды в открытом пьезометре выше уровня воды в сосуде на величину h₁, а точка А расположена выше точки В на величину h₂. Атмосферное давление p_атм = 98,1 кПа, удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 2

Задача 3

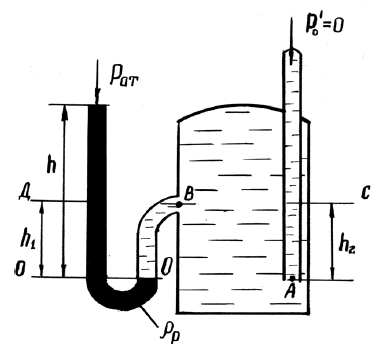
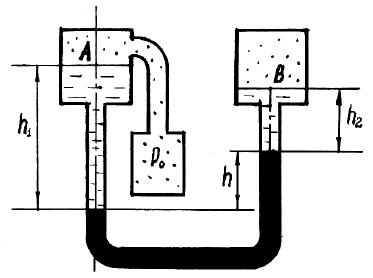
Определить абсолютное гидростатическое давление в точке А закрытого резервуара с водой (рис. 1.3), если высота столба ртути в трубке дифманометра h, а линия раздела между ртутью и водой расположена ниже точки В на величину h₁, точка В – выше точки А на величину h₂. Атмосферное давление p_ат = 98,1 кПа, удельный вес воды γ_в = 9,81 кН/м³, удельный вес ртути γ_р = 133,4 кН/м³.

Купить задачу 3

Задача 4

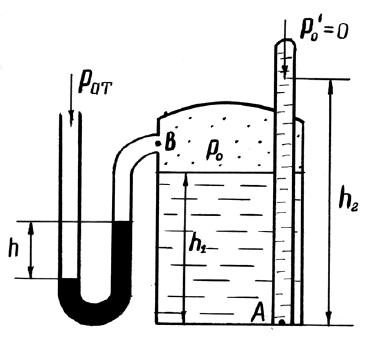
Закрытый резервуар снабжен дифманометром, установленным в точке В, и закрытым пьезометром (рис. 1.4). Определить приведенную пьезометрическую высоту поднятия пресной воды h_x в закрытом пьезометре (соответствующую абсолютному гидростатическому давлению в точке А), если высота столба ртути в трубке дифманометра h, а точка А расположена на глубине h₁ от свободной поверхности. Атмосферное давление p_атм = 98,1 кПа, удельный вес воды γ_в = 9,81 кН/м³, удельный вес ртути γ_р = 133,4 кН/м³.

Купить задачу 4

Задача 5

Определить высоту подъема жидкости в пьезометре h_х если высота столба ртути в трубке дифманометра h₁, а точка А расположена на глубине h₂ от свободной поверхности (рис. 1.5). Атмосферное давление p_атм = 98,1 кПа, удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 5

Задача 6

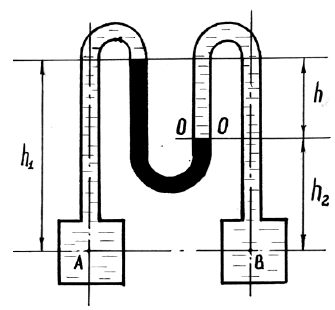
К двум резервуарам А и В, заполненным водой, присоединен дифференциальный ртутный манометр (Рис. 1.6). Составить уравнение равновесия относительно плоскости равного давления и определить разность давлений в резервуарах А и В, если расстояние от оси резервуара до мениска ртути равны h₁ и h₂. Удельный вес воды γ_в = 9,81 кН/м³, удельный вес ртути γ_р = 133,4 кН/м³.

Купить задачу 6

Задача 7

Определить разность показаний ртутного дифманометра h_x, составив уравнение равновесия относительно плоскости равного давления. Дифманометр подключен к двум закрытым резервуарам с водой (рис. 1.7), давление в резервуаре А равно p_А, а в резервуаре В – p_В. Удельный вес воды γ_в = 9,81 кН/м³, удельный вес ртути γ_р = 133,4 кН/м³.

Купить задачу 7

Задача 8

Резервуары А и В частично заполнены водой разной плотности и газом, причем, к резервуару А подключен баллон с газом (рис. 1.8). Какое необходимо создать давление p₀ в баллоне, чтобы получить давление p_В на свободной поверхности в резервуаре В, если высота столба ртути в трубке дифманометра h, а расстоянии от оси резервуаров до мениска ртути равны h₁ и h₂? Удельный вес ртути γ_р = 133,4 кН/м³, плотность воды в резервуаре А – ρ_А = 998 кг/м³, в резервуаре В – ρ_В = 1029 кг/м³.

Купить задачу 8

Задача 9

К двум резервуарам А и В заполненным нефтью, присоединен дифференциальный ртутный манометр (рис. 1.9). Определить разность давлений в точках А и В, составив уравнение равновесия относительно плоскости равного давления. Разность показаний манометра h₁ – h₂ = h. Удельный вес ртути γ_р = 133,4 кН/м³, нефти – γ_н = 8,83 кН/м³.

Купить задачу 9

Задача 10

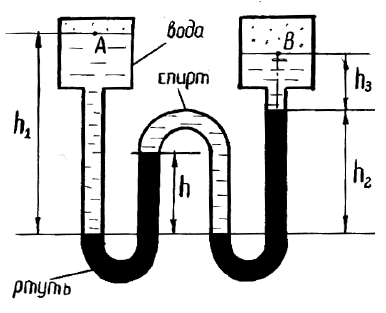
Резервуары А и В частично заполнены водой и газом (рис. 1.10). Определить избыточное давление газа на поверхности воды закрытого резервуара В, если избыточное давление на поверхности воды в закрытом резервуаре А равно p_А, разность уровней ртути в двухколенном дифманометре h, мениск ртути в левой трубке манометра ниже уровня воды на величину h₁, в правой трубке – h₃ = 0,25h₁, высота подъема ртути в правой трубке манометра h₂. Пространство между уровнями ртути в манометре заполнено этиловым спиртом. Удельный вес ртути γ_р = 133,4 кН/м³, воды γ_в = 9,81 кН/м³, этилового спирта γ_с = 7,74 кН/м³.

Купить задачу 10

Задача 11

Определить сжимающее усилие P₁ гидравлического пресса с диаметрами поршней D и d (рис. 2.1), используемого для получения виноградного сока, если к малому поршню приложена сила P.

Купить задачу 11

Задача 12

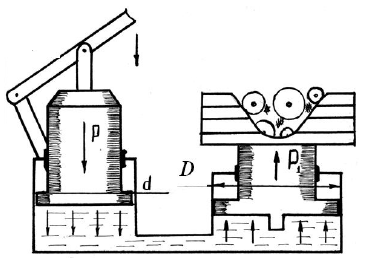
При ремонте сельскохозяйственных машин и оборудования широко используется гидравлический домкрат, принципиальная схема которого приведена на рис. 2.2. Определить усилие P, которое необходимо приложить к малому поршню, чтобы поднять груз весом G. Диаметрами поршней D и d.

Купить задачу 12

Задача 16

Определить давление пара p в цилиндре поршневого парового насоса (рис. 2.6), необходимое для подачи воды на высоту H = 60 м, если диаметры цилиндров D и d.

Купить задачу 16

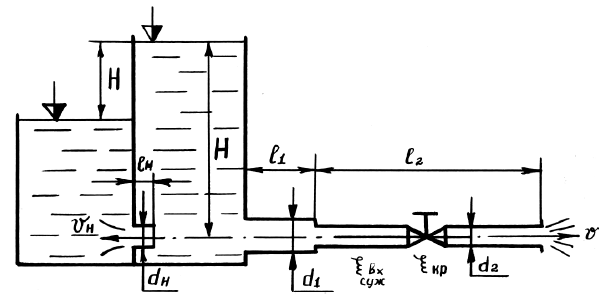
Задача 17

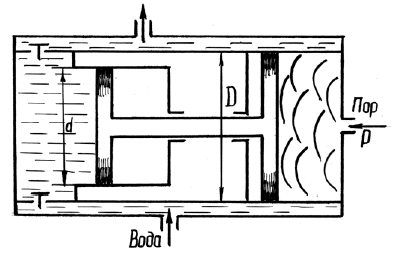
Для повышения гидростатического давления применяется мультипликатор – повыситель давления (рис. 2.7), давление на входе которого p₁ = 20 кПа, а диаметры поршней D и d. Определить давление жидкости p₂ на выходе из мультипликатора.

Купить задачу 17

Задача 18

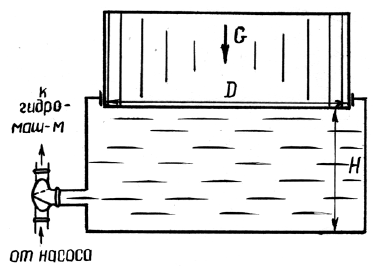
Для накопления энергии используется грузовой гидравлический аккумулятор (рис. 2.8), вес плунжера которого равен G, диаметр – D. Определить запасаемую аккумулятором энергию при ходе плунжера H = 6 м.

Купить задачу 18

Задача 22

Плоский квадратный щит установлен с углом наклона к горизонту α (рис. 3.2). Глубина воды перед щитом – h₁, за щитом h₂, ширина щита – b. Определить силу избыточного гидростатического давления и центр давления жидкости на щит. Удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 22

Задача 23

Для сброса излишков воды используется донный водовыпуск, прямоугольный затвор которого имеет размеры a и b (рис. 3.3). Глубина воды от ее свободной поверхности до нижней кромки затвора h₁, угол наклона затвора α, плотность воды ρ = 1000 кг/м³. Определить силу абсолютного гидростатического давления жидкости на затвор водовыпуска.

Купить задачу 23

Задача 27

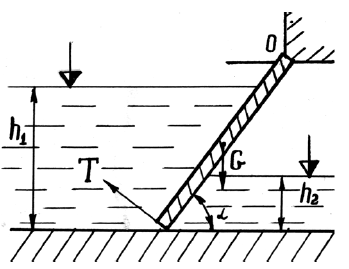
Прямоугольный щит перекрывает отверстие в теле плотины (рис. 3.7). Щит установлен с углом наклона α, имеет высоту a, ширину b и толщину c = 0,25b. Нижняя кромка щита находится в воде на глубине h₁, масса щита m = 2 т. Определить силу тяги T, которая необходима для поднятия щита вверх, принимая коэффициент трения скольжения его направляющих f = 0,3. Удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 27

Задача 29

Для создания подпора в реке применяется плотина Шануана (рис. 3.9), представляющая собой плоский прямоугольный щит, который может вращаться вокруг горизонтальной оси О. Угол наклона щита α, глубина воды перед щитом h₁, а за щитом – h₂. Определить положение оси вращения щита (х₀), при котором в случае увеличения верхнего уровня воды выше плотины, щит опрокидывался бы под ее давлением.

Купить задачу 29

Задача 30

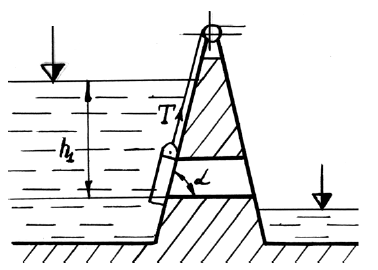
Ирригационный канал перегораживается плоским квадратным наклонным щитом шириной a (рис. 3.10). Угол наклона щита α, глубина воды перед щитом h₁, a за ним – h₂, вес щита G = 20 кН. Определить, пренебрегая трением в шарнире, начальную силу тяги T, которую необходимо приложить для подъема щита.

Купить задачу 30

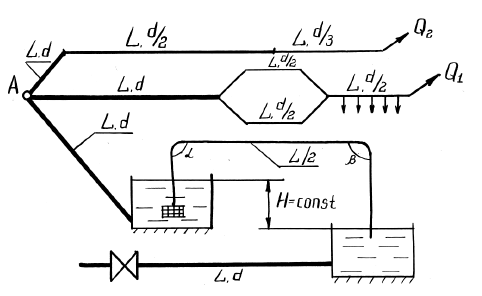
Задача 32

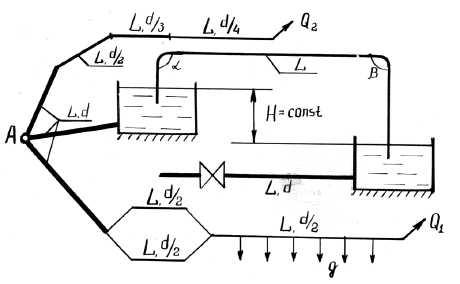
Из источника А вода подается в разветвленную сеть (рис. 4.2). Магистральный трубопровод имеет последовательные участки длиной L, диаметрами d, d/2, d/3 и параллельные ветви, имеющие диаметры d/2. На одном из участков имеется путевой объемный расход воды q. По ответвлению вода подается в резервуар, который связан посредством сифонного трубопровода с другим резервуаром. Разница уровней в резервуарах H. Сифонный трубопровод выполнен с углами поворота α и β, имеет сетку с обратным клапаном. От нижнего резервуара отходит трубопровод с толщиной стенок e, в котором перед закрытием задвижки имеется давление p₀. Трубы в сети чугунные.

Требуется:

1. Определить распределение расхода в ветвях трубопровода с объемным расходом Q₁ на параллельных участках.
2. Определить потери напора на последовательных участках трубопровода с объемным расходом Q₂.
3. Определить, при какой начальной скорости υ₀ движения воды в чугунном трубопроводе давление при мгновенном закрытии задвижки достигнет величины p.
4. Определить диаметр сифона.

 

Купить задачу 32

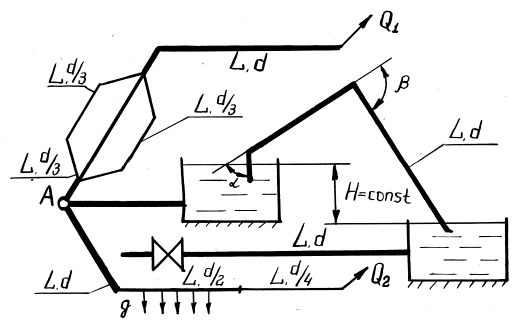
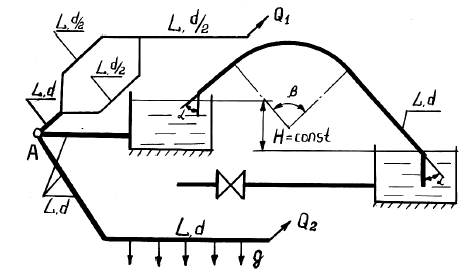
Задача 33

В тепличном комбинате стальные трубопроводы для подачи питательного раствора (кинематическую вязкость ν принять равной 0,01 см²/с) разветвляются на три участка: последовательный с объемным расходом Q₂, параллельный с объемным расходом Q₁ и участок с объемным расходом Q, в конце которого установлена задвижка (рис. 4.3). Резервуары с питательным раствором сообщаются посредством сифона с углами поворота α и β. Движение в сифоне происходит с разностью напоров – Н. Последовательные и параллельные участки трубопроводов имеют длину L, диаметры d, d/2, d/3, d/4. На одном из участков имеется путевой объемный расход q.

Требуется:

1. Определить повышение давления Δр в стальном трубопроводе длиной L, с толщиной e и объемным расходом Q.
2. Определить распределение расхода в параллельных ветвях участка.
3. Определить объемный расход в сифоне.
4. Определить потери напора h₁, h₂, h₃ на последовательных участках трубопровода, имеющего объемный расход Q₂.

 

Купить задачу 33

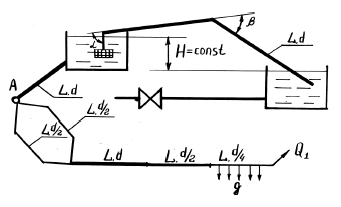
Задача 34

Из пункта А (рис. 4.4) вода подается по чугунному трубопроводу в открытые емкости с разницей между верхней и нижней отметками – Н. Емкости сообщаются посредством сифона, выполненного из чугунных труб с углами поворота α и β. Трубопровод с объемным расходом Q₂ состоит из последовательных участков каждый длиной L и диаметрами d, d/2, d/4. Параллельный участок состоит из двух ветвей каждая длиной L и диаметром d/2.От нижней емкости отходит чугунный трубопровод, заканчивающийся задвижкой.

Требуется:

1. Определить потери напора по длине трубопровода при последовательном соединении.
2. Определить распределение расхода в трубопроводе на участках при параллельном соединении.
3. Определить напряжение σ в стенках толщиной е чугунного трубопровода диаметром d при внезапном его закрытии, если начальное избыточное давление в трубопроводе – р₀, начальная скорость – V₀.
4. Определить диаметр сифона при заданном объемном расходе Q_сиф.

 

Купить задачу 34

Задача 35

Из нефтехранилища А (рис. 4.5) нефть подается в накопительный резервуар, где поддерживается постоянный уровень. Из резервуара-накопителя нефть поступает в приемный резервуар под напором Н при помощи сифонного нефтепровода, причем труба отходит под углом α и имеет острые входные кромки. Сифонный чугунный трубопровод в верхней точке имеет плавный поворот на угол β. От хранилища А по чугунному трубопроводу нефть подводится к двум параллельным ветвям каждая длиной L и диаметром d/2. Система последовательно соединенных трубопроводов состоит из двух участков каждый длиной L, диаметрами d, d/2. Третий участок, кроме транзитного объемного расхода Q₁ имеет равномерно распределенный путевой объемный расход q.

Требуется:

1. Определить объемный расход в сифоне при заданном диаметре d.
2. Определить повышение давления Δp в чугунном трубопроводе с толщиной стенки e при объемном расходе Q.
3. Определить потери напора по длине нефтепровода на участках последовательного соединения с объемным расходом Q₂.
4. Определить распределение расхода нефти на параллельных участках нефтепровода, если объемный расход в конце его Q₁.

 

Купить задачу 35

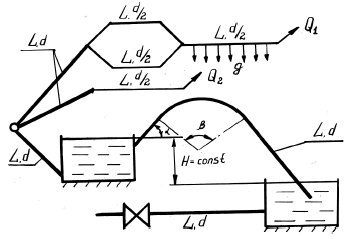
Задача 36

Водораспределительная сеть, выполненная из чугунных трубопроводов, состоит из последовательных и параллельных участков, двух резервуаров, сообщающихся при помощи сифона, и отходящего от нижнего резервуара чугунного трубопровода с задвижкой (рис. 4.6). Один из последовательных участков имеет путевой объемный расход q. Горизонты уровней в резервуарах разнятся на величину H. Сифонный трубопровод с углами поворота α и β имеет обратный клапан с сеткой и пропускает объемный расход Q_сиф.

Требуется:

1. Определить распределение объемного расхода Q₁ в трубопроводах при параллельном соединении.
2. Определить диаметр сифона.
3. Определить потери напора по длине последовательно соединенных участков трубопровода, пропускающего объемный расход Q₂.
4. Определить начальную скорость V₀ в чугунном трубопроводе с толщиной стенок e, если после внезапного закрытия задвижки давление перед задвижкой будет p, а перед закрытием давление было p₀.

 

Купить задачу 36

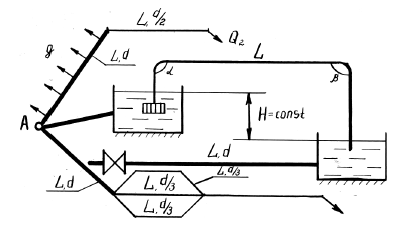
Задача 38

Из водоисточника А (рис. 4.8) вода подается в накопительный резервуар, где поддерживается постоянный уровень. Из резервуара-накопителя вода поступает в приемный резервуар при помощи стального сифонного водопровода, имеющего углы поворота α и β. Стальной трубопровод диаметром d, отходящий от нижнего резервуара, заканчивается задвижкой. Система последовательно соединенных трубопроводов с длиной L и диаметрами d, d/2, d/3, d/4 пропускает транзитом из источника А объемный расход Q₂ к потребителю. Система трубопроводов с параллельными ветвями заканчивается последовательным участком с равномерно распределенным путевым объемным расходом q.

Требуется:

1. Определить повышение давления Δp в трубопроводе диаметрами d, длиной L, имеющем толщину стенок e, при внезапном закрытии задвижки, если объемный расход составляет Q.
2. Определить диаметр сифона, пропускающего объемный расход Q_сиф.
3. Определить распределение расхода в трубопроводах с параллельным соединением.
4. Определить потери напора на участках трубопровода при последовательном соединении.

 

Купить задачу 38

Задача 39

Два хранилища с керосином сообщаются со стальным сифоном, имеющим длину L и диаметр d (рис. 4.9). Отметки уровней керосина в хранилищах отличаются на величину Н. От нижнего хранилища отходит стальная труба диаметром d с задвижкой и толщиной стенок е. От пункта А отходят стальные трубопроводы с последовательным и параллельным соединением, имеющие объемные расходы соответственно Q₂ и Q₁. На втором участке последовательного соединения производится равномерная путевая раздача воды q.

Требуется:

1. Определить объемный расход в сифоне при заданном диаметре.
2. Определить потери напора на участках с последовательным соединением.
3. Определить, при какой начальной скорости V₀ движения керосина в стальном трубопроводе давление при мгновенном закрытии задвижки достигает величины р, если перед закрытием задвижки в трубопроводе – давление р₀.
4. Определить распределение расхода в параллельных ветвях трубопровода.

 

Купить задачу 39

Задача 40

Из источника А (рис. 4.10) вода подается по чугунному трубопроводу в водоем, где поддерживается постоянный уровень и который сообщен с другим водоемом посредством сифона. Чугунный сифон имеет диаметр d и углы поворота α и β. От второго водоема отходит чугунный трубопровод диаметром d с толщиной стенки е, в котором перед закрытием задвижки создается давление p₀. Другой участок системы водоснабжения имеет трубопроводы с параллельным и последовательным соединениями. Путевой объемный расход в конце последовательного участка составляет q.

Требуется:

1. Определить распределение расхода в параллельных ветвях трубопровода.
2. Определить потери напора в последовательно соединенных трубопроводах.
3. Определить объемный расход в сифоне Q.
4. Определить напряжение σ в стенках трубопровода при внезапном закрытии задвижки, если до закрытия вода в нем двигалась со скоростью V₀.

 

Купить задачу 40

Задача 41

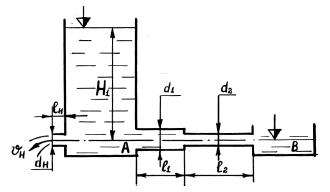
Из открытого резервуара при постоянном напоре H₁ вытекает вода с одной стороны в атмосферу по короткому трубопроводу диаметром d₁ и длиной l₁ с диффузором на конце, площадь живого сечения которого за расширением ω₂ = 2ω₁ с другой стороны через затопленный внешний цилиндрический насадок (насадок Вентури) диаметром d_н и длиной l_н = 5d₁ в другой резервуар. Разность уровней в резервуарах Н. Температура воды t = 50 °С.

Определить:

1. Скорость истечения υ₂ и расход воды по короткому трубопроводу Q₂, если коэффициент сопротивления задвижки ξ_з = 2,5, диффузора ξ_диф = 0,9. Коэффициент гидравлического трения определить по заданной шероховатости стенок трубы Δ = 1 мм.
2. Расход через насадок диаметром d_н и длиной l_н, если коэффициент расхода насадка μ = 0,82.
3. Сравнить расход воды через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.

 

Купить задачу 41

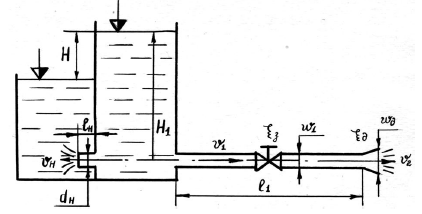
Задача 42

К открытому резервуару подсоединены короткий стальной трубопровод, состоящий из двух участков длиной l₁ и l₂, диаметрами d₁ и d₂ и внутренний цилиндрический насадок (насадок Борда) диаметром d_н и длиной l_н = 5d_н (рис. 5.2). Истечение по короткому трубопроводу происходит в атмосферу под постоянным напором H₁, коэффициент сопротивления крана принять равным ξ_кр = 3.

Определить:

1. Скорость и расход воды, вытекающей из трубопровода при температуре воды t = 10 °C.
2. Расход через насадок при разности уровней в резервуарах H, если коэффициент расхода насадка μ_н = 0,71.
3. Сравнить расход воды через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.

 

Купить задачу 42

Задача 43

К закрытому резервуару, на свободной поверхности которого действует манометрическое давление p_м, подсоединены чугунный трубопровод переменного сечения с диаметрами d₁, d₂ заканчивающимся соплом диаметром d_с = d₁, и конически сходящийся насадок с диаметром выходного сечения d_н и длиной l_н = 5d_н. Трубопровод и насадок подсоединены на глубине H₁. На первом участке длиной l₁ установлен вентиль, коэффициент сопротивления которого ζ_в = 4. Длина второго участка l₂. Коэффициент сопротивления сопла ζ_с = 0,06, сжатие струи на выходе из сопла отсутствует (рис. 5.3).

Определить:

1. Скорость истечения V и расход Q вытекающий из сопла воды при температуре t = +10 °С и постоянном напоре H₁.
2. Расход воды через затопленный насадок при разности уровней в резервуарах H, если коэффициент расхода насадка μ_н = 0,94.
3. Сравнить расход воды, проходящий через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.

 

Купить задачу 43

Задача 44

Истечение происходит из открытого резервуара при постоянном напоре воды H₁ по короткому трубопроводу переменного поперечного сечения с диаметрами d₁ и d₂ в атмосферу и из конически расходящегося насадка с диаметром выходного сечения d_н и длиной l_н = 5d_н под уровень (рис. 5.4). Разность уровней – H₂ = 1,5 м.

На втором участке трубопровода имеются два колена с плавным поворотом, коэффициент сопротивления каждого ξ_к = 0,15, и задвижки, коэффициент сопротивления которой ξ_з = 8,0. Коэффициент гидравлического трения на первом участке длиной l₁ принять равным λ₁ = 0,04, на втором участке длиной l₂ – λ₂ = 0,025.

Определить:

1. Скорость истечения V₂ и расход Q₂ через трубопровод.
2. Скорость истечения и расход через затопленный конически расходящийся насадок, если коэффициент скорости и коэффициент расхода насадка равны и составляют φ_н = μ_н = 0,45.
3. Сравнить скорость и расход через насадок со скоростью и расходом через отверстие в тонкой стенке того же диаметра. Коэффициент скорости для отверстия φ = 0,97, а коэффициент расхода μ = 0,62.

 

Купить задачу 44

Задача 45

Из открытого резервуара по короткому стальному трубопроводу постоянного поперечного сечения d₁ и длиной l₁, который заканчивается соплом диаметром d_с = 0,5d₁, вытекает вода при t = +30 °C в атмосферу. Истечение происходит под напором H₁ (рис. 5.5). Коэффициент сопротивления крана принять равным ξ_к = 2,5. С другой стороны к резервуару подсоединен коноидальный насадок диаметром выходного сопла d_н и длиной l_н = 5d_н.

Определить:

1. Скорость истечения из сопла V_с и расход воды по короткому трубопроводу Q_с.
2. Расход воды через затопленный коноидальный насадок при разности уровней в резервуарах H, если коэффициент расхода насадка μ = 0,97.
3. Сравнить расход воды через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.
4. 

Купить задачу 45

Задача 46

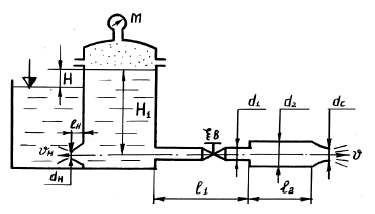
Вода при температуре t = 15 °C из резервуара А подается в резервуар В по трубопроводу, состоящему из двух участков длиной l₁ и l₂ диаметрами d₁ и d₂. Коэффициент гидравлического трения принять равным λ = 0,03. С другой стороны на том же уровне к резервуару А подсоединен внешний цилиндрический насадок (насадок Вентури) диаметром d_н и длиной l_н = 5d_н (Рис. 5.6).

Определить:

1. Напор H₁, который нужно поддерживать в баке A, чтобы наполнить бак В, объемом W_в = 18 м³ за 30 мин. Коэффициент гидравлического трения принять равным λ = 0,03. Коэффициент потерь при входе в трубу принять равным ζ_вх = 0,5.
2. Скорость истечения воды через насадок в предположении, что в резервуаре А находится вода под напором H₁ определенным из предыдущего условия. Коэффициент скорости насадка φ_н принять равным φ_н = 0,82.
3. Сравнить скорость истечения из насадка со скоростью истечения через отверстие в тонкой стенке того же диаметра, если φ_отв = 0,62.

 

Купить задачу 46

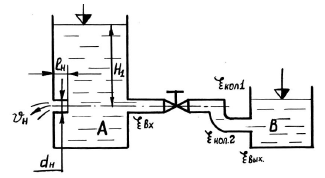
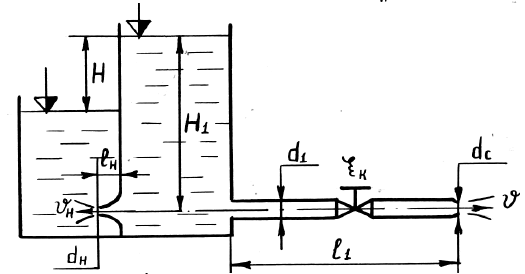
Задача 47

Вода при температуре t = 20 °C из резервуара А подается в резервуар В со скоростью V = 0,5 м/с по стальному трубопроводу диаметром d₁ и длиной l₁. Уровень воды в баке А поддерживается постоянным. Коэффициенты сопротивления: входа в трубу ζ_вх = 0,5; крана ζ_кр = 1,5; колена без закругления ζ_кол1 = 0,25; колена с закруглением ζ_кол2 = 0,14. На глубине H₁ к резервуару подсоединен внутренний цилиндрический насадок (насадок Борда) диаметром d_н и длиной l_н = 5d_н (рис. 5.7).

Определить:

1. Время заполнения водой резервуара В объемом W_в = 1,15 м³ и потери напора в трубопроводе.
2. Скорость истечения воды из насадка, если коэффициент скорости для насадка φ_н = 0,71.
3. Сравнить скорость истечения из насадка со скоростью истечения из отверстия в тонкой стенке того же диаметра, если φ_от = 0,62.

 

Купить задачу 47

Задача 48

Из резервуара А, заполненного водой на высоту H₁, и находящегося под манометрическим давлением p_м, вода подается по стальному трубопроводу длиной l₁ и диаметром d₁ в резервуар В на высоту H. К резервуару А на глубине H₁ подсоединен конически сходящийся насадок с диаметром выходного сечения d_н и длиной l_н = 5d_н (рис. 5.8). Коэффициенты сопротивлений задвижки ξ_з = 9,0; каждого колена с закруглением ξ_к = 0,25; коэффициент гидравлического трения λ = 0,04. Кинематическая вязкость воды ν = 1,24 · 10^-6 м²/с. Скоростным напором и изменением уровня в баке В пренебречь.

Определить:

1. Режим течения, расход Q и скорость протекающей по трубопроводу воды.
2. Скорость и расход, проходящий через конически сходящийся насадок, если коэффициент скорости для насадка φ_н = 0,96, а коэффициент расхода μ_н = 0,94.
3. Сравнить скорость и расход воды через насадок со скоростью и расходом через отверстие в тонкой стенке такого же диаметра, если коэффициент скорости для отверстия φ = 0,97, а коэффициент расхода μ = 0,62.

 

Купить задачу 48

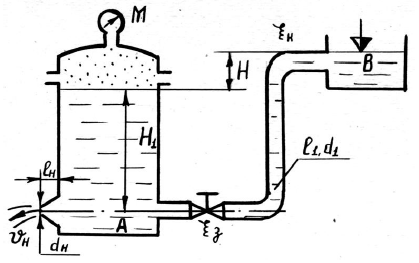
Задача 50

Вода при температуре t = 20 °C подается из резервуара А в резервуар В по короткому трубопроводу, состоящему из двух участков длиной l₁ и l₂ диаметрами d₁ и d₂. Разность уровней в резервуарах равна H. На глубине H₁ к резервуару А подсоединен коноидальный насадок диаметром выходного сечения d_н и длиной l_н = 5d_н (рис. 5.10).

Определить:

1. Расход Q, поступающий в резервуар В по короткому трубопроводу, если коэффициент сопротивления крана ζ_кр = 4,2, коэффициент гидравлического трения λ = 0,032.
2. Расход воды через коноидальный насадок, если коэффициент расхода насадка μ_н = 0,97.
3. Сравнить расход через коноидальный насадок с расходом через отверстие в тонкой стенке, если коэффициент для отверстия μ = 0,62.

 

Купить задачу 50

Задач, которых нет, Вы можете заказать