Р.12
РСам.СГАСУ
Задачи на эпюры и построение линий полного и пьезометрического напоров
Часть задач есть решенные, контакты
1. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТИ
Задача 1-1
Определить плотность жидкости, полученной смешиванием жидкости объемом V1, плотностью ρ1 и жидкости объемом V2, плотностью ρ2. Исходные данные представлены в таблице 1.1.
Задача 1-2
Жидкость, имеющая плотность ρ и объем V, получена смешиванием масла плотностью ρ1 с маслом плотностью ρ2. Определить объем масел, составляющих эту жидкость. Исходные данные представлены в таблице 1.2.
Задача 1-3
Определить плотность жидкости, полученной смешиванием двух минеральных масел плотностью ρ1 и ρ2. Объем первого масла составляет 40% объема второго. Исходные данные представлены в таблице 1.3.
Задача 1-4
Определить плотность рабочих жидкостей при различных температурах. Результаты расчета занести в таблицу 1.4. Температурный коэффициент объемного расширения всех масел βТ = 8,75 × 10-4 С-1. Значения ρ20 при температуре +20 °С этих масел приведены в приложении (см. табл. П2.5).
Купить задачу 1-4 (вариант 1)
Задача 1-5
При температуре +20ºC масла М-10-В2, МГ-46-В (МГ-30) и МГ-15-В(с) (ВМГЗ) занимают объем V0. Определить объем, который они будут занимать при температуре –40 и +80ºC, если температурный коэффициент объемного расширения всех масел βT = 8,75 · 10–4ºC–1. Исходные данные представлены в таблице 1.5.
Купить задачу 1-5 (вариант 1)
Задача 1-6
Минеральное масло и вода в гидроцилиндрах при атмосферном давлении p0 занимают объем V0. Определить, какой объем будут занимать эти жидкости при давлении p, если коэффициент сжимаемости минерального масла βV = 6,6 · 10–10 м2/Н, а воды — βV = 4,7 · 10–10 м2/Н.
Деформацией стенок гидроцилиндра пренебречь. Исходные данные представлены в таблице 1.6.
Купить задачу 1-6 (вариант 1)
Задача 1-7
На какую величину переместится шток гидроцилиндра диаметром D с запертым в нем при атмосферном давлении объемом минерального масла V0 = 18 л, если к штоку приложить усилие Т? Коэффициент сжимаемости масла βV = 6,6 · 10-10 м2/Н. Деформацией стенок гидроцилиндра пренебречь. Исходные данные представлены в таблице 1.7.
Купить задачу 1-7 (вариант 1)
Задача 1-8
Стальной трубопровод длиной l и диаметром d при атмосферном давлении p0 полностью заполнен минеральным маслом. Определить, какой дополнительный объем масла необходимо подать в полость трубы при гидравлическом испытании под давлением p. Коэффициент сжимаемости масла равен βV = 6,6 · 10-10 м2/Н. Деформацией стенок трубы пренебречь. Исходные данные представлены в таблице.
Купить задачу 1-8 (вариант 4)
Купить задачу 1-8 (вариант 7)
Задача 1-9
Какое количество тепла Q необходимо израсходовать, чтобы за один час нагреть рабочую жидкость массой mж от температуры T0 до температуры Tж? Средняя удельная теплоемкость жидкости cж = 1,85 · 103 Дж/(кг · ºC). Теплообмен с внешней средой не учитывать. Исходные данные представлены в таблице 1.9.
Купить задачу 1-9 (вариант 1)
Задача 1-10
Какое количество тепла Q необходимо израсходовать, чтобы за полтора часа нагреть рабочую жидкость массой mж от температуры T0 до температуры Tж с учетом теплообмена с внешней средой? Коэффициент теплоотдачи k = 7,5 Вт/(м2 · ºC), а средняя удельная теплоемкость жидкости cж = 1,85 · 103 Дж/(кг · ºC). Массу емкости, в которой находится жидкость, не учитывать. Исходные данные представлены в таблице 1.10.
Задача 1-11
Вода при температуре TºC имеет удельный вес γ Н/м3. Определить ее относительный вес δ и плотность ρ. Исходные данные представлены в таблице 1.11.
Задача 1—12
Вертикальный цилиндрический резервуар заполнен нефтью при температуре T1 °С на высоту h. Определить положение уровня нефти при повышении температуры до T2 °С. Расширение резервуара не учитывать. Коэффициент температурного расширения βT = 0,00072 °С. Исходные данные представлены в таблице 1.12.
Купить задачу 1-12 (вариант 1)
Купить задачу 1-12 (вариант 2)
Задача 1-13
В отопительной системе (котел, радиаторы и трубопроводы) небольшого дома содержится V м3 воды. Сколько воды дополнительно войдет в расширительный сосуд при нагревании от T1 до T2 °C? Исходные данные приведены в таблице.
Купить задачу 1-13 (вариант 2)
Купить задачу 1-13 (вариант 7)
Задача 1-14
Стальной трубопровод диаметром d м и длиной м, проложенный открыто, находится под давлением p кг/см2 при температуре воды T1ºC. Определить давление воды в водопроводе при повышении температуры до T2ºC в результате наружного нагрева. Исходные данные представлены в таблице 1.14.
Задача 1-15
Емкость, заполненная нефтью, находится под давлением p кг/см2. После выпуска ΔV м3 нефти давление в емкости упало до p1 кг/см2. Определить объем емкости V, если коэффициент объемного расширения нефти составляет βV = 7,4 · 10–8 м2/кг. Исходные данные представлены в таблице 1.15.
Задача 1-16
В отопительный котел поступает вода в количестве Q, м3/ч, при температуре воды T1ºC. На сколько увеличится расход вытекающей из котла воды, если она прогревается в нем до температуры T2ºC? Исходные данные представлены в таблице 1.16.
Задача 1-17
Трубопровод длиной l м и внутренним диаметром d мм перед гидравлическим испытанием заполнен водой при атмосферном давлении. Сколько нужно добавить в трубопровод воды, чтобы давление в нем повысилось до величины p2 кг/см2? Температура воды T °C. Исходные данные представлены в таблице.
Купить задачу 1-17 (вариант 1)
Купить задачу 1-17 (вариант 2)
Часть задач есть решенные, контакты
2. ГИДРОСТАТИКА
ДАВЛЕНИЕ В ПОКОЯЩЕЙСЯ ЖИДКОСТИ
Задача 2-1
На поршень одного из сообщающихся сосудов, наполненных водой, действует сила F1. Какую силу F2 следует приложить ко второму поршню, чтобы уровень воды h под ним был выше уровня воды под первым поршнем, если диаметр первого поршня d1, второго d2 (рис. 2.6)? Исходные данные приведены в таблице 2.1.
Купить задачу 2-1 (вариант 1)
Задача 2-2
На поршень одного из сообщающихся сосудов, наполненных бензином, действует сила F1, а на второй F2 (рис. 2.6). Определить диаметр поршня d2. Исходные данные приведены в таблице 2.2.
Купить задачу 2-2 (вариант 1)
Купить задачу 2-2 (вариант 2)
Задача 2-3
Определить высоту h уровня нефти при следующих данных: F2, F1, d1, d2 (рис. 2.6). Исходные данные приведены в таблице 2.3.
Задача 2-4
Найти силу F2, действующую на поршень одного из сообщающихся сосудов, наполненных керосином, если известны F1, h, d1, d2 (рис. 2.6). Исходные данные приведены в таблице 2.4.
Купить задачу 2-4 (вариант 1)
Задача 2-5
К закрытому резервуару с водой присоединены два ртутных пьезометра (рис. 2.7). Определить глубину погружения нижнего пьезометра h, если известны показания ртутных пьезометров h1, h2, глубина погружения верхнего пьезометра a. Исходные данные приведены в таблице 2.5.
Купить задачу 2-5 (вариант 1)
Купить задачу 2-5 (вариант 2)
Задача 2-6
Определить высоту h, на которую может поднять воду прямодействующий паровой насос при следующих данных: диаметры цилиндров d1 и d2; манометрическое давление в паровом цилиндре pм. Исходные данные представлены в таблице.
Купить задачу 2-6 (вариант 1)
Купить задачу 2-6 (вариант 4)
Задача 2-7
Определить диаметр d2 прямодействующего парового насоса при следующих данных: диаметр цилиндра d1, манометрическое давление в паровом цилиндре pм, высота подъема воды в пьезометре h. Исходные данные приведены в таблице.
Купить задачу 2-7 (вариант 1)
Купить задачу 2-7 (вариант 2)
Задача 2-8
Определить диаметр поршня d1 прямодействующего парового насоса при следующих данных, приведенных в таблице.
Купить задачу 2-8 (вариант 2)
Задача 2-9
Зная высоту подъема воды в пьезометре h, диаметры поршней d1 и d2, найти pм (рис. 2.8). Исходные данные приведены в таблице 2.9.
Купить задачу 2-9 (вариант 1)
Задача 2-10
Неподвижный сосуд, составленный из двух цилиндров с диаметрами d1 и d2, заполнен минеральным маслом (γ = 900 кг/м3), находится в равновесии (рис.2.9). Определить, какая сила F1 должна быть приложена к малому поршню, чтобы при силе F2, приложенной к большому поршню, расстояние между поршнями было X + Y. Исходные данные приведены в таблице 2.10.
Задача 2-11
Неподвижный сосуд, указанный на рисунке 2.9, составленный из двух цилиндров с диаметрами d1 и d2, заполнен минеральным маслом (γ = 850 кг/м3), удерживаемым поршнями, на которые действуют силы F1 и F2. Определить положение X и Y поршней относительно торцевой стенки сосуда, если объем жидкости между поршнями V. Исходные данные приведены в таблице 2.11.
Купить задачу 2-11 (вариант 1)
Задача 2-12
Определить силу F2, приложенную к большому поршню (см. рис. 2.9), если сосуд заполнен минеральным маслом (γ = 870 кг/м3) при известных F1, d1, d2, V. Исходные данные приведены в таблице 2.12.
Купить задачу 2-12 (вариант 1)
Задача 2-13
В открытые сообщающиеся сосуды налиты жидкости разного удельного веса γ1 и γ2. Найти высоту h, если известна h1 (рис. 2.10). Исходные данные приведены в таблице 2.13.
Задача 2-14
В открытые сообщающиеся сосуды налиты жидкости разного удельного веса γ1 и γ2 (рис. 2.10). Найти высоты h1 и h2 над плоскостью раздела жидкостей, если разность уровней h. Исходные данные приведены в таблице 2.14.
Задача 2-15
Найти диаметр d2 поршня правого сосуда, наполненного водой, указанного на рисунке 2.11, чтобы уравновесить давление воды на поршень левого сосуда при исходных данных, приведенных в таблице 2.15.
Задача 2-16
Определить, на какую высоту поднимается вода h2 в пьезометре, чтобы уравновесить давление воды на поршень левого сосуда и при действии на него силы F (рис. 2.11). Исходные данные приведены в таблице 2.16.
Задача 2-17
Какую силу F нужно приложить к поршню левого сосуда, наполненного водой (см. рис. 2.11), чтобы уравновесить давление воды на поршень правого сосуда? Исходные данные приведены в таблице 2.17.
Купить задачу 2-17 (вариант 1)
Задача 2-18
Найти диаметр d1 поршня левого сосуда, наполненного водой, чтобы уравновесить давление воды на поршень правого сосуда (см. рис. 2.11). Исходные данные приведены в таблице 2.18.
Купить задачу 2-18 (вариант 1)
Задача 2-19
Найти диаметр d3 поршня левого сосуда, наполненного водой, чтобы уравновесить давление воды на поршень правого сосуда (см. рис. 2.11). Исходные данные приведены в таблице 2.19.
Купить задачу 2-19 (вариант 3)
Купить задачу 2-19 (вариант 4)
Задача 2-20
Определить высоту h1 (см. рис. 2.11), чтобы уравновесить давление воды в сообщающихся сосудах при данных, приведенных в таблице 2.20.
Купить задачу 2-20 (вариант 1)
Задача 2-21
Закрытый сосуд, указанный на рисунке 2.12, наполнен водой на глубину H. Давление на свободной поверхности p0. Определить уровень жидкости в открытой трубке над уровнем воды в сосуде hр. Определить полное и избыточное давление у дна сосуда. Построить эпюру гидростатического давления воды на плоскую стенку АВ. Исходные данные приведены в таблице 2.21.
Купить задачу 2-21 (вариант 1)
Задача 2-22
В закрытом сосуде находится жидкость плотностью ρ = 999,6 кг/м3. Глубина наполнения сосуда H, высота поднятия жидкости в пьезометре hр. Определить: 1) давление p0 на свободной поверхности сосуда; 2) полное и избыточное давление у дна сосуда в трех системах измерения (в мегапаскалях (МПа), технических атмосферах и метрах водяного столба (м вод. ст.).
Купить задачу 2-22 (вариант 1)
Купить задачу 2-22 (вариант 3)
Задача 2-23
В закрытом сосуде находится жидкость плотностью ρ = 999,6 кг/м3. Глубина наполнения сосуда H. Давление на поверхности p0. Определить: 1) высоту поднятия hр жидкости в открытой трубке над уровнем ее в сосуде (давление в открытом конце трубки – атмосферное pатм); 2) полное и избыточное давление у дна сосуда в трех системах измерения (в мегапаскалях (МПа), технических атмосферах и метрах водяного столба (м вод. ст.). Построить эпюру гидростатического давления жидкости на плоскую поверхность АВ.
Купить задачу 2-23 (вариант 1)
Купить задачу 2-23 (вариант 2)
Задача 2-24
На какой высоте h над точкой А стенки резервуара (рис. 2.13) находится свободная поверхность воды, если манометр показывает давление pм? Давление на свободной поверхности воды p0. Построить эпюру гидростатического давления воды на плоскую поверхность ВС. Исходные данные приведены в таблице 2.24.
Купить задачу 2-24 (вариант 2)
Задача 2-25
К боковой стенке резервуара, наполненного водой (рис. 2.14), присоединена в точке B пьезометрическая трубка на глубине от свободной поверхности h.
Внешнее давление на свободной поверхности p0. Найти высоту подъема жидкости в пьезометре hp. Построить эпюру гидростатического давления жидкости на плоскую поверхность AC. Исходные данные приведены в таблице 2.25.
Купить задачу 2-25 (вариант 1)
Задача 2-26
К боковой стенке резервуара (рис. 2.14), наполненного водой, установлена в точке B пьезометрическая трубка на глубине от свободной поверхности h.
Определить внешнее давление на свободной поверхности жидкости в резервуаре p0, если под действием этого давления вода в трубке поднялась на высоту hp. Построить эпюру гидростатического давления воды на плоскую поверхность AC. Исходные данные приведены в таблице 2.26.
Задача 2-27
Определить вакуумметрическое и абсолютное давление в резервуаре А, указанном на рисунке, если жидкость с объемным весом γ = 9810 Н/м3 поднялась по обратному пьезометру на высоту hвак. Построить эпюру давления жидкости на стенку CD. Исходные данные представлены в таблице.
Купить задачу 2-27 (вариант 1)
Купить задачу 2-27 (вариант 4)
Задача 2-28
Определить силу давления керосина на дно сосуда и показание манометра (рис.), если на поршень диаметром d1 давит сила F. Диаметр сосуда d2, глубина керосина h. Объемный вес γ = 7810 Н/м3. Построить эпюру давления жидкости на стенку АВ. Исходные данные приведены в таблице.
Купить задачу 2-28 (вариант 1)
Купить задачу 2-28 (вариант 5)
Задача 2-29
Определить, какую силу F нужно приложить к правому поршню сообщающихся сосудов, указанных на рисунке 2.17, при известных значениях d1, d2, d3, pм, h. Исходные данные приведены в таблице 2.29.
Задача 2-30
Определить диаметр d1 одного из сообщающихся сосудов (рис. 2.17), наполненных керосином, под действием силы F, приложенной к поршню правого сосуда, если известны d2, d3, pм, h. Исходные данные приведены в таблице 2.30.
Задача 2-31
Определить манометрическое давление pм в верхней части одного из сообщающихся сосудов, наполненных водой, под действием силы F, приложенной к поршню правого сосуда, если известны d1, d2, d3, h.
Исходные данные приведены в таблице.
Купить задачу 2-31 (вариант 3)
Задача 2-32
Определить высоту h сообщающихся сосудах, наполненных бензином, под действием силы F, приложенной к поршню второго сосуда, если известны d1, d2, d3, pм (рис. 2.17). Исходные данные приведены в таблице 2.32.
Задача 2-33
Определить диаметр d3 в верхней части одного из сообщающихся сосудов, наполненных нефтью, под действием силы F, приложенной к поршню правого сосуда, если известны d1, d2, pм, h (см. рис. 2.17). Исходные данные приведены в таблице 2.33.
Задача 2-34
Определить диаметр d2 одного из сообщающихся сосудов, наполненных минеральным маслом, под действием силы F, приложенной к поршню правого сосуда, если известны d1, d3, pм, h (см. рис. 2.17). Исходные данные приведены в таблице 2.34.
Купить задачу 2-34 (вариант 1)
Задача 2-35
Определить глубину воды h в закрытом сосуде, указанном на рисунке 2.18, если ртутный манометр показывает разность уровней ртути hр, при известных значениях p0, a, b. Построить эпюру гидростатического давления жидкости на плоскую поверхность AB. Исходные данные приведены в таблице 2.35.
Задача 2-36
Зная давление p0 на поверхности воды в закрытом сосуде (рис. 2.18), найти hр при известных значениях h, a, b. Исходные данные приведены в таблице 2.36.
Задача 2-37
Зная высоты h, a, b, определить давление p0 на поверхность воды в закрытом сосуде, если ртутный манометр показывает hр. Построить эпюру гидростатического давления на плоскую поверхность AB (рис. 2.18). Исходные данные приведены в таблице 2.37.
Задача 2-38
Найти давление автола в точке А при γавт = 8829 Н/м3, если известны h1 и h2 (рис. 2.19). Исходные данные приведены в таблице 2.38.
Купить задачу 2-38 (вариант 1)
Купить задачу 2-38 (вариант 2)
Купить задачу 2-38 (вариант 4)
Задача 2-39
Определить, на какой высоте h2 установится уровень ртути в пьезометре, если при манометрическом давлении pA в точке A и показании h1 система находится в равновесии при γавт = 8829 Н/м3 (рис. 2.19). Исходные данные приведены в таблице 2.39.
Купить задачу 2-39 (вариант 1)
Задача 2-40
Определить диаметр плунжера d, указанного на рисунке, если его заглубление a, сила давления на плунжер F, высота подъема воды в пьезометрической трубке h. Собственный вес плунжера не учитывать. Построить эпюру давления воды на стенку АВ при l = 0,8 м. Исходные данные приведены в таблице.
Купить задачу 2-40 (вариант 3)
Задача 2-41
Определить заглубление плунжера a, если высота подъема воды в пьезометрической трубке h, диаметр плунжера d, сила давления на плунжер F (рис. 2.20).
Начертить эпюру давления на стенку AB при = 0,9 м. Исходные данные приведены в таблице 2.41.
Задача 2-42
Определить величину давления p0 воды в сосуде и высоту h1, если высота поднятия ртути в ртутном манометре h2. Построить эпюру давления жидкости на плоскую стенку AB = 200 см (рис. 2.21). Исходные данные приведены в таблице 2.42.
Задача 2-43
Определить избыточное давление p0 в сосуде A по показанию жидкостного манометра, если в левом открытом колене над ртутью налито масло (ρм = 870 кг/м3), в правом — вода (рис. 2.22). Исходные данные приведены в таблице 2.43.
Задача 2-44
Определить величину давления p0 на поверхности воды в сосуде, если в трубке ртутного манометра жидкость поднялась на высоту h, поверхность воды в сосуде находится на расстоянии H от нижнего уровня ртути в колене манометра (рис. 2.23). Исходные данные приведены в таблице 2.44.
Задача 2-45
На горизонтальной плите установлен стальной сосуд без дна в форме усеченного конуса с толщиной стенки δ. Определить, при каком уровне воды h в сосуде он оторвется от плиты, если известны d, D, H. Исходные данные приведены в таблице.
Купить задачу 2-45 (вариант 2)
Купить задачу 2-45 (вариант 6)
Задача 2-46
Определить величину и направление равнодействующей силы давления воды на цилиндрический затвор, перекрывающий прямоугольное донное отверстие высотой h = D и шириной b (рис. 2.25). Глубина воды слева — H1, справа — H2 = D/2. Исходные данные приведены в таблице 2.46.
Задача 2-47
Определить силу давления воды на крышку закрытого круглого сосуда, в котором вода находится под манометрическим давлением pм (рис. 2.26). Исходные данные приведены в таблице 2.47.
Купить задачу 2-47 (вариант 1)
Купить задачу 2-47 (вариант 5)
Задача 2-48
Шаровой клапан закрывает отверстие в баке (рис. 2.27). Пренебрегая весом шара и рычагов, определить минимальную силу F, необходимую для герметичного закрытия клапана. Исходные данные приведены в таблице 2.48.
Купить задачу 2-48 (вариант 2)
Задача 2-49
Шаровой клапан прижимается к седлу пружиной и давлением жидкости p1. Диаметр шара — D, диаметр отверстия седла — d. Определить силу, с которой пружина должна прижимать шар к седлу, если давление под клапаном p2 (рис. 2.28). Исходные данные приведены в таблице 2.49.
Купить задачу 2-49 (вариант 2)
Задача 2-50
Для контроля уровня топлива (γт = 890 кг/м3) в открытом подземном резервуаре, указанном на рисунке 2.29, использована U-образная трубка с ртутным затвором. При полностью заправленном резервуаре разность уровней топлива в баке и указателе равна h1.
Определить, как изменится уровень топлива в указателе при понижении уровня в баке на 1 м. Исходные данные приведены в таблице 2.50.
Купить задачу 2-50 (вариант 1)
Купить задачу 2-50 (вариант 3)
Задача 2-51
В большом сосуде, частично заполненном жидкостью, плавает опрокинутый вверх дном малый сосуд весом G. Определить разность уровней воды в сосудах h1, выяснить так же какое усилие F способно погрузить малый сосуд на дно большого, если при убранном поршне малый сосуд возвышается над уровнем воды на высоту h2. Процесс сжатия считать изотермическим. Исходные данные приведены в таблице.
Купить задачу 2-51 (вариант 2)
Купить задачу 2-51 (вариант 4)
Задача 2-52
Пружинный манометр подключен к сосуду с водой на высоте h от дна (рис. 2.31). Центр манометра находится выше точки подключения его к сосуду на Z. Определить: а) избыточное давление на дно при показании манометра pм; б) показание манометра при абсолютном давлении на поверхность воды в сосуде p0, атмосферном давлении pатм = 100 кПа и заданном H. Исходные данные приведены в таблице 2.52.
Задача 2-53
Определить вакуум в резервуаре, указанном на рисунке 2.32, если заданы h1 и h2 и атмосферное давление pатм = 100 кПа. Исходные данные приведены в таблице 2.53.
Купить задачу 2-53 (вариант 1)
Купить задачу 2-53 (вариант 2)
Задача 2-54
Круглое отверстие диаметром d в вертикальной стенке резервуара с водой перекрыто плоским клапаном (рис. 2.33). Найти величину и точку приложения силы, прижимающей клапан к стенке, если центр отверстия находится ниже свободной поверхности жидкости на величину h. Исходные данные приведены в таблице 2.54.
Задача 2-55
U-образный ртутный манометр подключен к закрытому резервуару, заполненному водой (рис. 2.34). Определить давление на поверхности воды в резервуаре, если известны h1, h2 и pатм. Исходные данные приведены в таблице 2.55.
Задача 2-56
Каково показание h2 U-образного ртутного манометра, подключённого к резервуару с водой, если известны h1 + h2 = 600 мм; p0 = 0,75 атм; pа = 9,81 · 104 Па?
Купить задачу 2-56 (вариант 2)
Купить задачу 2-56 (вариант 3)
Купить задачу 2-56 (вариант 4)
Задача 2-57
Определить разность давления в резервуарах A и B, заполненных бензином (рис. 2.36), если показание дифференциального ртутного манометра hр задано. Исходные данные приведены в таблице 2.57.
Задача 2-58
Малые перепады давления измеряются микроманометром. По заданному показанию определить измеряемое давление (рис. 2.37). Исходные данные приведены в таблице 2.58.
Купить задачу 2-58 (вариант 3)
Задача 2-59
В пьезометрическую трубку диаметром 6 мм попал пузырек воздуха, касающийся стенок и имеющий форму шара (рис. 2.38). Определить относительную погрешность показаний h пьезометра. Исходные данные приведены в таблице 2.59.
Купить задачу 2-59 (вариант 1)
Купить задачу 2-59 (вариант 2)
Задача 2-60
В цилиндрический сосуд при закрытом кране B и открытом кране A наливается ртуть при атмосферном давлении до высоты h1 (рис. 2.39). Высота сосуда — H. Затем кран A закрывается, а кран B открывается.
Ртуть начинает вытекать из сосуда в атмосферу. Предполагая, что процесс происходит изотермически, определить вакуум в сосуде при новом положении уровня h2 в момент равновесия и величину h2. Исходные данные приведены в таблице 2.60.
Задача 2-61
Определить, на какой высоте Z устанавливается уровень ртути в пьезометре, если при манометрическом давлении pA в трубе A и показании h система находится в равновесии (рис. 2.40). Исходные данные приведены в таблице 2.61.
Купить задачу 2-61 (вариант 2)
Задача 2-62
Определить полное гидростатическое давление на дно сосуда прямоугольной формы, заполненного водой. Давление на свободной поверхности — атмосферное. Глубина в сосуде — h. Вычислить толщину стенок сосуда из условия равнопрочности, если материал — сталь. Исходные данные приведены в таблице 2.62.
Купить задачу 2-62 (вариант 3)
Задача 2-63
Определить при помощи дифференциального манометра разность давлений в точках B и A двух трубопроводов, заполненных водой (рис. 2.41). Высота столба ртути — h. Удельный вес ртути — γрт = 13600 кг/м3; воды — γв = 9810 Н/м3. Исходные данные приведены в таблице 2.63.
Купить задачу 2-63 (вариант 3)
Задача 2-64
Высота столба ртути, измеренная по дифференциальному манометру, равна 25 см. Вычислить высоту столба h, которая установится при той же разнице давлений, если центр трубопровода B будет расположен выше точки A на величину Z (рис. 2.42). Исходные данные приведены в таблице 2.64.
Купить задачу 2-64 (вариант 1)
Задача 2-65
Для измерения уровня нефти H в открытом резервуаре установлена вертикальная труба, практически достигающая дна резервуара, в которую подается воздух с очень малой скоростью (рис. 2.43). Определить уровень нефти по показанию ртутного дифманометра. Исходные данные приведены в таблице 2.65.
Купить задачу 2-65 (вариант 2)
Купить задачу 2-65 (вариант 4)
Задача 2-66
Для определения ускорения горизонтально движущегося тела может быть использована закрепленная на нем трубка малого диаметра, U-образной формы, заполненная жидкостью (рис. 2.44). Определить ускорение a тела при разности уровней h и длине горизонтального участка . Исходные данные приведены в таблице 2.66.
Задача 2-67
К резервуару, заполненному газом под давлением p/γ, присоединена трубка, опущенная в сосуд с ртутью (рис. 2.45). Требуется: а) определить давление p в резервуаре, если ртуть в трубке поднялась на высоту h; б) найти высоту h, на которую поднимется ртуть в трубке, если давление в резервуаре равно p/γ. Исходные данные приведены в таблице 2.67.
Купить задачу 2-67 (вариант 2)
Задача 2-68
Для схемы, показанной на рисунке 2.46, превышение точки В над точкой А равно Z = 15 см. В качестве рабочей жидкости применен керосин. Определить разность давлений в баллонах А и В при показании прибора h, если в баллонах – нефть. Исходные данные приведены в таблице 2.68.
Купить задачу 2-68 (вариант 1)
Купить задачу 2-68 (вариант 2)
Купить задачу 2-68 (вариант 4)
Задача 2-69
Чему равно манометрическое давление в сосуде по показанию дифманометра, если в левом его колене над ртутью налита вода, а в самом сосуде находится масло (рис. 2.47)? Исходные данные приведены в таблице 2.69.
Купить задачу 2-69 (вариант 4)
Задача 2-70
В цилиндрический бак диаметром D до уровня H налиты вода и бензин (рис. 2.48). Уровень воды в пьезометре ниже уровня бензина на h. Определить вес находящегося в баке бензина, если ρб = 700 кг/м3. Исходные данные приведены в таблице 2.70.
Задача 2-71
Определить абсолютное давление воздуха в баке p1, если при атмосферном давлении, соответствующем hа = 760 мм рт. ст., показание ртутного манометра hрт, высота h (рис. 2.49). Каково при этом показание пружинного вакуумметра? Плотность ртути ρрт = 13 600 кг/м3. Исходные данные приведены в таблице 2.71.
Задача 2-72
При перекрытом кране трубопровода K определить абсолютное давление в резервуаре, зарытом на глубину H (рис. 2.50), если показание вакуумметра, установленного на высоте h, равно pвак. Атмосферное давление соответствует hа = 740 мм рт. ст. Плотность бензина ρб = 700 кг/м3. Исходные данные приведены в таблице 2.72.
Купить задачу 2-72 (вариант 1)
Купить задачу 2-72 (вариант 4)
Задача 2-73
В сосуде A и в трубе вода находится в покое; показание ртутного прибора hрт. Определить высоту H, если известна величина h (рис. 2.51). Исходные данные приведены в таблице 2.73.
Купить задачу 2-73 (вариант 2)
Купить задачу 2-73 (вариант 3)
Задача 2-74
В герметичном сосуде-питателе A, приведенном на рисунке 2.52, находится расплавленный баббит (ρ = 8000 кг/м3). При показании вакуумметра (B) pвак заполнение разливочного ковша Б прекратилось. При известном значении H определить высоту уровня баббита h в сосуде-питателе A. Исходные данные приведены в таблице 2.74.
Купить задачу 2-74 (вариант 4)
Задача 2-75
Избыточный напор газа на первом этаже дома составляет h1. Определить избыточный напор газа h2 на высоте H (рис. 2.53), считая плотность воздуха и газа неизменными. Плотность газа ρг = 0,70 кг/м3, плотность воздуха ρв = 1,29 кг/м3. Исходные данные приведены в таблице 2.75.
Купить задачу 2-75 (вариант 2)
Часть задач есть решенные, контакты
СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКИЕ ПОВЕРХНОСТИ
Задача 2-76
Определить усилие T, необходимое для открытия прямоугольного затвора размером b×h, шарнирно прикрепленного своей верхней кромкой, если известны глубина воды перед плотиной H, расстояние a, угол α = 45° (рис. 2.58). Исходные данные приведены в таблице 2.76.
Купить задачу 2-76 (вариант 1)
Купить задачу 2-76 (вариант 2)
Задача 2-77
Плоский щит в виде равнобедренного треугольника размерами b и h закрывает отверстие в стенке (рис. 2.59). Определить минимально необходимое натяжение T каната и реакцию R на оси поворота O щита. Построить эпюру избыточного давления на щит. Исходные данные приведены в таблице 2.77.
Купить задачу 2-77 (вариант 1)
Купить задачу 2-77 (вариант 2)
Задача 2-78
Прямоугольный щит размером b×h закрывает отверстие в плоской стенке (рис. 2.60). Определить минимально необходимое натяжение T каната и реакцию R на оси поворота О щита. Построить эпюру избыточного давления воды на щит ОА. Исходные данные приведены в таблице 2.78.
Купить задачу 2-78 (вариант 1)
Задача 2-79
Круглое отверстие диаметром d в тонкой стенке резервуара закрыто поворотным щитом. Определить натяжение троса T, если известны H и углы α1 = α2 = 45°. Трос прикреплен к щиту на расстоянии 2/3(d) от шарнира О. Построить эпюру гидростатического давления на ОА. Исходные данные приведены в таблице
Купить задачу 2-79 (вариант 1)
Купить задачу 2-79 (вариант 5)
Задача 2-80
Круглое отверстие диаметром d в наклонной стенке резервуара с водой закрыто поворотным щитом. (рис. 2.62) Определить натяжение каната T. Построить эпюру давления воды на затвор ОА. Исходные данные приведены в таблице 2.80
Купить задачу 2-80 (вариант 1)
Купить задачу 2-80 (вариант 2)
Задача 2-81
Квадратное отверстие со стороной a в наклонной стенке резервуара с водой закрыто поворотным щитом. Определить расстояние b при натяжении каната T. Построить эпюру давления воды на затвор ОА. Исходные данные приведены в таблице 2.81.
Купить задачу 2-81 (вариант 1)
Задача 2-82
Определить усилие T, необходимое для подъема щита, находящегося под давлением воды, если глубина воды перед щитом h, масса щита m = 300 кг, ширина b, коэффициент трения f = 0,3 (по направляющим). Найти точку приложения силы давления воды на щит. Построить эпюру гидростатического давления на ОА. Исходные данные приведены в таблице.
Купить задачу 2-82 (вариант 1)
Задача 2-83
Донное отверстие плотины перекрывается плоским прямоугольным щитом, шарнирно прикрепленным к телу плотины своей верхней кромкой.
Определить, какое усилие T нужно приложить к тросу для открытия щита при следующих данных: глубина погружения нижней кромки щита H, высота щита h, ширина щита B, угол между направлением троса и горизонтом α. Построить эпюру давления воды на щит ОА. Исходные данные приведены в таблице.
Купить задачу 2-83 (вариант 1)
Купить задачу 2-83 (вариант 5)
Задача 2-84
Определить суммарную силу давления воды на щит AB шириной b (рис. 2.66). Построить эпюру гидростатического давления на стенку AB и проверить результаты аналитического и графического исследования (решить двумя способами). Исходные данные приведены в таблице 2.84.
Купить задачу 2-84 (вариант 1)
Задача 2-85
Канал прямоугольной формы перегорожен вертикальным щитом АВ. Глубина воды перед щитом H1, за щитом – H2. Ширина щита равна ширине канала b. Определить силы давления F1 и F2, действующие слева и справа, и точки их приложения, а также величину равнодействующей этих сил F и точку ее приложения (два способа решения). Построить эпюры гидростатического давления на щит АВ. Исходные данные приведены в таблице.
Купить задачу 2-85 (вариант 1)
Купить задачу 2-85 (вариант 3)
Задача 2-86
Квадратное отверстие со стороной a в наклонной стенке резервуара с водой закрыто поворотным щитом, шарнирно закрепленным в точке О (рис. 2.68). Определить натяжение каната T. Построить эпюру давления воды на щит ОА. Исходные данные приведены в таблице 2.86.
Купить задачу 2-86 (вариант 1)
Купить задачу 2-86 (вариант 2)
Купить задачу 2-86 (вариант 4)
Задача 2-87
В перегородке, разделяющей резервуар на две части, имеется прямоугольное отверстие, которое закрывается поворотным щитом OA высотой h и шириной b (рис. 2.69). Определить силу T, которую нужно приложить к тросу для поворота щита, и реакцию донного порога R. Исходные данные приведены в таблице 2.87.
Купить задачу 2-87 (вариант 4)
Задача 2-88
В перегородке, разделяющей резервуар на две части, имеется квадратное отверстие со стороной a (рис. 2.70). Определить силу T, которую нужно приложить к тросу для поворота шарнирного щита. Найти реакцию донного порога R «жидкость–вода». Исходные данные приведены в таблице 2.88.
Купить задачу 2-88 (вариант 1)
Задача 2-89
Определить натяжение троса, удерживающего прямоугольный щит шириной b, при глубине воды перед щитом h (рис. 2.71), пренебрегая собственной массой щита, если угол наклона щита к горизонту β. Построить эпюру давления на щит. Исходные данные приведены в таблице 2.89.
Купить задачу 2-89 (вариант 1)
Задача 2-90
Определить тяговые усилия T1 и T2 в двух случаях для круглых плоских поворотных затворов диаметром d (рис. 2.72). Глубина погружения верхней кромки затвора a. Исходные данные приведены в таблице 2.90.
Купить задачу 2-90 (вариант 1)
Задача 2-91
В перегородке, разделяющей резервуар на две части, имеется квадратное отверстие со стороной a.
Определить силу Т, которую нужно приложить к тросу для поворота шарнирного щита. Найти реакцию донного порога R «жидкость-вода». Исходные данные приведены в таблице.
Купить задачу 2-91 (вариант 3)
Задача 2-92
Вход в туннель перекрыт квадратным плоским стальным затвором со стороной a и толщиной b. Глубина воды над поверхностью щита h1, сила давления воды в туннеле F2. Коэффициент трения в пазах f. Определить подъемное усилие T и точку приложения силы давления.
Купить задачу 2-92 (вариант 1)
Купить задачу 2-92 (вариант 2)
Купить задачу 2-92 (вариант 3)
Задача 2-93
Вход в туннель перекрыт квадратным плоским стальным затвором со стороной a и толщиной b (рис. 2.74). Глубина воды над поверхностью щита h1, а глубина воды в туннеле h2. Коэффициент трения в пазах f.
Определить подъемное усилие T и точку приложения равнодействующей силы давления. Исходные данные приведены в таблице 2.93.
Купить задачу 2-93 (вариант 3)
Задача 2-94
Поворотный клапан закрывает выход из бензохранилища в трубу квадратного сечения h × h (рис. 2.75). Определить, какую силу T нужно приложить к тросу для открытия клапана, если манометрическое давление pм. Исходные данные приведены в таблице 2.94.
Купить задачу 2-94 (вариант 1)
Купить задачу 2-94 (вариант 3)
Купить задачу 2-94 (вариант 4)
Задача 2-95
Поворотный щит закрывает выход из бензохранилища в трубу квадратного сечения h х h (рис. 2.75).
Определить силу T и давление паров бензина в резервуаре pм, если сила давления на затвор F. Исходные данные приведены в таблице 2.95.
Купить задачу 2-95 (вариант 1)
Купить задачу 2-95 (вариант 3)
Задача 2-96
Поворотный клапан AO закрывает выход из бензохранилища в трубу квадратного сечения со стороной h (рис. 2.75). Клапан опирается на срез трубы, сделанный под углом α. Определить (без учета трения) силу T натяжения троса, необходимую для открытия клапана, если давление над уровнем бензина (ρб = 700 кг/м3) по манометру составляет pм, а сила давления на затвор F. Построить эпюру избыточного давления бензина на затвор АО. Исходные данные приведены в таблице 2.96.
Купить задачу 2-96 (вариант 1)
Задача 2-97
Определить усилие T, необходимое для подъема плоского квадратного щита, расположенного под углом α к горизонту и находящегося под давлением воды (рис. 2.76), если сторона квадрата a, высота l, масса щита m = 15 кг, коэффициент трения щита в направляющих f = 0,3. Найти центр давления и построить эпюру гидростатического давления воды на щит АВ. Исходные данные приведены в таблице 2.97.
Купить задачу 2-97 (вариант 2)
Купить задачу 2-97 (вариант 4)
Задача 2-98
Построить эпюру гидростатического давления на стенку ломаного очертания (рис. 2.77) и определить суммарную силу давления воды F и точку ее приложения на участке 2 – 3 стенки. Исходные данные приведены в таблице 2.98.
Купить задачу 2-98 (вариант 1)
Купить задачу 2-98 (вариант 2)
Задача 2-99
Определить реакции верхнего и нижнего опорных брусьев, на которые опирается щит, перекрывающий прямоугольное отверстие плотины шириной b (рис. 2.78). Построить эпюры гидростатического давления на щит. Исходные данные приведены в таблице 2.99.
Задача 2-100
Определить реакции верхнего и нижнего опорных брусьев, на которые опирается щит, перекрывающий прямоугольное отверстие плотины шириной b, при известных значениях F1, F2, a (рис. 2.78). Исходные данные приведены в таблице 2.100.
Купить задачу 2-100 (вариант 1)
Купить задачу 2-100 (вариант 2)
Задача 2-101
Определить горизонтальную силу Fx, стремящуюся сдвинуть каменную плотину (рис. 2.79), если длина плотины (ширина стенки) b, глубина воды перед плотиной h. Исходные данные приведены в таблице 2.101.
Задача 2-102
Отверстие в перегородке замкнутого сосуда закрыто крышкой диаметром d (рис. 2.80). Левая секция залита ртутью до центра отверстия. Газ над ртутью находится под абсолютным давлением p1, в правой секции — газ под абсолютным давлением p2 = 0. Определить силу давления F на крышку. Исходные данные приведены в таблице 2.102.
Купить задачу 2-102 (вариант 1)
Задача 2-103
Диаметр затвора d (рис. 2.80). Определить давление газа над ртутью p1, находящегося в левой части сосуда, если давление газа справа p2 = 0,01 МПа. Ртуть залита до центра отверстия. Сила давления на крышку имеет значение F. Исходные данные приведены в таблице 2.103.
Купить задачу 2-103 (вариант 1)
Купить задачу 2-103 (вариант 3)
Купить задачу 2-103 (вариант 4)
Задача 2-104
Клапанный затвор OA (рис. 2.81), имеющий плоскую поверхность размером a х b, создает подпор воды H. Определить силу натяжения троса T, удерживающего затвор в заданном положении. Исходные данные приведены в таблице 2.104.
Задача 2-105
Определить вертикальное усилие T, необходимое для открывания поворотной чугунной крышки, закрывающей прямоугольное отверстие высотой h, шириной b, если ее собственный вес G (рис. 2.82). Исходные данные приведены в таблице 2.105.
Купить задачу 2-105 (вариант 2)
Купить задачу 2-105 (вариант 4)
Задача 2-106
Определить равнодействующую силу избыточного давления воды на плоский затвор CB, перекрывающий отверстие трубы, имеющей треугольное поперечное сечение (рис. 2.83), и найти координату точки ее приложения YD. Построить эпюру по указанному сечению. Исходные данные приведены в таблице 2.106.
Задача 2-107
Определить равнодействующую силу избыточного давления воды на плоский затвор, перекрывающий отверстие трубы, имеющей прямоугольное поперечное сечение (рис. 2.84). Найти координату точки ее приложения YD. Построить эпюру по указанному сечению. Исходные данные приведены в таблице 2.107.
Купить задачу 2-107 (вариант 3)
Задача 2-108
Определить равнодействующую силу избыточного давления воды на плоский затвор, перекрывающий отверстие трубы, имеющей треугольное поперечное сечение (рис. 2.85). Найти координату YD точки приложения силы избыточного давления и построить эпюру по указанному сечению. Исходные данные приведены в таблице 2.108.
Купить задачу 2-108 (вариант 2)
Купить задачу 2-108 (вариант 3)
Задача 2-109
Определить равнодействующую силу избыточного давления воды на плоский вертикальный затвор, перекрывающий отверстие круглой трубы (рис. 2.86).
Найти координату YD точки приложения равнодействующей силы давления F и построить эпюру по указанному сечению. Исходные данные приведены в таблице 2.109.
Купить задачу 2-109 (вариант 1)
Задача 2-110
Закрытый резервуар разделен на две части перегородкой, имеющей квадратное отверстие (рис. 2.87). Давление над жидкостью в левой части резервуара определяется по вакуумметру V, а в правой — по манометру М. Найти значение результирующей силы давления на крышку F и координату YD точки ее приложения, построить эпюры давления на крышку. Исходные данные приведены в таблице 2.110.
Задача 2-111
Определить, на каком расстоянии X должна располагаться ось поворотного прямоугольного щитка размером х b (рис. 2.88), чтобы момент суммарной силы давления воды относительно оси щитка (точка O) был равен нулю. Построить эпюру гидростатического давления на затвор. Исходные данные приведены в таблице 2.111.
Купить задачу 2-111 (вариант 2)
Задача 2-112
Закрытый резервуар с жидкостью (рис. 2.89) разделен на две части плоской перегородкой, имеющей прямоугольное отверстие со сторонами a х b. Давление над жидкостью в левой части резервуара определяется показанием манометра М, а в правой — вакуумметра V.
Найти значение результирующей силы F и точку ее приложения YD. Исходные данные приведены в таблице 2.112.
Задача 2-113
Прямоугольный повторный щит размером х b закрывает выпускное отверстие плотины при уровнях воды H1 и H2 (рис. 2.90). Определить начальную силу T натяжения троса лебедки. С какой силой щит прижимается к порогу B в закрытом положении? Построить эпюры избыточного давления воды на щит OB. Исходные данные приведены в таблице 2.113.
Купить задачу 2-113 (вариант 1)
Купить задачу 2-113 (вариант 2)
Задача 2-114
Вертикальный щит, состоящий из пятидосок одинаковой ширины a, сдерживает столб воды высотой H (рис. 2.91). Определить силу давления воды на щит и на каждую доску щита в отдельности, если b = 1,6 м. Исходные данные приведены в таблице 2.114.
Задача 2-115
В перегородке, разделяющей резервуар на две части (рис. 2.92), устроен вырез, который закрывается прямоугольным щитом. Найти, на каком расстоянии X должна быть расположена ось поворота щита, чтобы он автоматически открывался при уровне воды в правой камере H1, если с другой стороны щита сохраняется постоянный уровень H2. Определить реакцию шарнира R0 при ширине щита b. Построить эпюры давления на щит OA. Исходные данные приведены в таблице 2.115.
Задача 2-116
Отверстие в боковой вертикальной стенке закрытого резервуара, представляющее собой равносторонний треугольник со стороной b, закрыто крышкой. Определить силу давления воды на крышку, если горизонтальное основание треугольного отверстия расположено на глубине H, а манометрическое давление на свободной поверхности – pм. Исходные данные приведены в таблице 2.116.
Купить задачу 2-116 (вариант 1)
Задача 2-117
Определить силу манометрического давления на дно сосудов, наполненных водой (рис. 2.94). Высота столбов — h, h1, h2. Площадь дна сосудов — W, а площадь сечения — W1. Найти силу, передаваемую в каждом случае на пол. Объясните гидростатический парадокс. Исходные данные приведены в таблице 2.117.
Задача 2-118
Определить отрывающее усилие, воспринимаемое болтами полусферической крышки диаметром d (рис. 2.95), если показание манометра — p0, а глубина воды — h. Исходные данные приведены в таблице 2.118.
Задача 2-119
Сосуд, установленный на полу и имеющий в нижней части на высоте h1 форму усеченного конуса (рис. 2.96), суживается от диаметра D до диаметра d. Сосуд закрыт и заполнен водой на высоту h. Манометрическое давление на свободной поверхности воды – p0. Определить: 1) силу манометрического давления на дно сосуда; 2) с какой силой сосуд давит на пол, пренебрегая весом сосуда. Исходные данные приведены в таблице.
Купить задачу 2-119 (вариант 5)
Задача 2-120
Определить сжимающее усилие F2 гидравлического пресса, если плечи рычага – a и b. Диаметры поршней D и d. Усилие, прилагаемое к рычагу – F, КПД пресса – η. Исходные данные приведены в таблице.
Купить задачу 2-120 (вариант 1)
Купить задачу 2-120 (вариант 3)
Задача 2-121
Для увеличения жесткости стенок металлического резервуара, заполненного водой на глубину H, они снабжены n горизонтальными поясами жесткости из профильного железа (рис. 2.98). Как должны быть расположены эти пояса, чтобы каждый из них воспринимал одинаковую нагрузку? Ширина резервуара b = 1 м. Исходные данные приведены в таблице 2.121.
Задача 2-122
Определить усилие F, действующее вдоль штока, если диаметр поршня – D, а давление, подводимое к гидроцилиндру справа, – p1, давление слева от поршня – p2. Диаметр штока – d. Трением пренебречь. Исходные данные приведены в таблице.
Купить задачу 2-122 (вариант 1)
Задача 2-123
Определить необходимую ширину B основания бетонной стенки треугольного профиля, удерживающей давление воды (рис. 2.100), из условия устойчивости ее на опрокидывание (противодавление снизу не учитывать). Коэффициент устойчивости на опрокидывание k = Mуд/Mопр (где Mуд — удерживающий момент). Толщина слоя воды H, длина бетонной стенки b, удельный вес бетона γб = 2,2 т/м3. Исходные данные приведены в таблице 2.123.
Задача 2-124
Определить силу давления воды на квадратный затвор, установленный в вертикальной стенке (рис. 2.101), если известно, что эксцентриситет равнодействующей силы давления равен e, а длина стороны квадрата — a. Исходные данные приведены в таблице 2.124.
Задача 2-125
Определить вертикальное подъемное усилие T щита шириной b, на который давит слой воды H (рис. 2.102). Возвышение оси шарнира над уровнем воды h. Угол наклона щита β. Весом щита и трением в шарнире пренебречь. Исходные данные приведены в таблице 2.125.
Купить задачу 2-125 (вариант 1)
Задача 2-126
В вертикальной стенке закрытого резервуара с нефтью (рис. 2.103) имеется квадратное отверстие (сторона квадрата — b). Определить: а) величину и точку приложения силы давления нефти на крышку, закрывающую это отверстие, если напор — H, а показание ртутного U-образного манометра равно h; б) при каком давлении p0 на свободную поверхность жидкости крышка будет находиться в равновесии. Для пунктов а) и б) построить эпюру давления на стенку для точек 1, 2, 3, 4. Исходные данные приведены в таблице 2.126.
Задача 2-127
Прямоугольный затвор с размерами a х b перекрывает выход из резервуара (рис. 2.104). На каком расстоянии x от дна необходимо расположить ось затвора O, чтобы при открывании его в начальный момент приходилось преодолевать только трение в шарнирах, если глубина воды в резервуаре равна H? Исходные данные приведены в таблице 2.127.
Купить задачу 2-127 (вариант 1)
Задача 2-128
Котел системы водяного отопления имеет люк для осмотра диаметром D (рис. 2.105). Люк закрыт плоской крышкой, прикрепленной 10 болтами. Определить диаметр болтов, если уровень воды в расширительном сосуде находится на высоте H, а центр тяжести крышки — на высоте h от осевой линии котла. Температура воды — T, °C. Допустимое напряжение материала болтов на разрыв равно [σR]. Исходные данные приведены в таблице 2.128.
Купить задачу 2-128 (вариант 2)
Задача 2-129
Два сосуда A и B одинакового диаметра заполнены водой (рис. 2.106). Сосуд A открыт. В верхнюю крышку сосуда B вставлена тонкая трубка. Определить силу давления воды на дно каждого сосуда и силу, передаваемую на пол, если известны HA, HB, h. Исходные данные приведены в таблице 2.129.
Купить задачу 2-129 (вариант 1)
Купить задачу 2-129 (вариант 3)
Задача 2-130
Гидравлический домкрат, указанный на рисунке 2.107, имеет диаметр большего поршня D, а диаметр меньшего поршня – d, КПД η = 0,8. Плечи рычага a и b. Определить: а) усилие F, которое необходимо приложить на конце рычага, чтобы поднять груз G; б) максимальную грузоподъемность домкрата G из условия, что усилие F на конце рычага не будет превышать 100 Н. Исходные данные приведены в таблице 2.130.
Купить задачу 2-130 (вариант 1)
Купить задачу 2-130 (вариант 2)
Задача 2-131
Тонкостенный резервуар с размерами B х B х H опущен в воду вверх дном (рис. 2.108). Определить: а) вес резервуара G, а также глубину его погружения h, если показание ртутного U-образного манометра hрт, а атмосферное давление pат = 98,1 кПа; б) показание ртутного U-образного манометра и глубину погружения резервуара h, если его вес — G. Исходные данные приведены в таблице 2.131.
Указание: подъемной силой следует пренебречь и считать, что сила тяжести резервуара приложена ко дну.
Задача 2-132
Круглое отверстие диаметром d в вертикальной стенке резервуара с водой перекрыто плоским клапаном (рис. 2.109). Найти величину и точку приложения силы, прижимающей клапан к стенке, если центр отверстия находится ниже свободной поверхности жидкости на величину h. Исходные данные приведены в таблице 2.132.
Задача 2-133
Определить натяжение троса, удерживающего прямоугольный щит шириной b, а также точку приложения силы давления воды (рис. 2.110) при глубине воды перед щитом h, если угол наклона щита к горизонту — α. Весом щита пренебречь. Исходные данные приведены в таблице 2.133.
Задача 2-134
Определить горизонтальную и вертикальную составляющие силы давления на 1 м ширины плотины (рис. 2.111), если известны h, 1, 2. Исходные данные приведены в таблице 2.134.
Задача 2-135
Определить силу давления жидкости (воды) на крышку люка диаметром D, указанного на рисунке 2.112, в следующих двух случаях: а) показание манометра pм и H0 известно; б) показание ртутного вакуумметра h при значении a (ρрт = 13 600 кг/м3) и известно H0. Исходные данные приведены в таблице 2.135.
Задача 2-136
Определить значение силы, действующей на перегородку, которая разделяет бак (рис. 2.113), если ее диаметр D, показания вакуумметра pвак, манометра pм. Исходные данные приведены в таблице 2.136.
Задача 2-137
Определить силу, действующую на болты 1 крышки бака, указанного на рисунке 2.114, если показание манометра pм, а угол наклона крышки α. В сечении бак имеет форму квадрата со стороной a. Исходные данные приведены в таблице 2.137.
Задача 2-138
Определить давление в гидросистеме и вес груза G, лежащего на поршне 2 (рис. 2.115), если для его подъема к поршню 1 приложена сила F. Диаметры поршней D и d. Разностью высот пренебречь. Исходные данные приведены в таблице 2.138.
Задача 2-139
Определить максимальную высоту Hmax, на которую можно подсасывать бензин поршневым насосом, если давление его насыщенных паров составляет hн.п.; а атмосферное давление hа = 700 мм рт. ст. Чему равна при этом сила вдоль штока, если известно H0, D и ρб = 700 кг/м3?
Задача 2-140
Определить силу F, необходимую для удержания поршня на высоте h2 над поверхностью воды в колодце (рис. 2.117). Над поршнем поднимается столб воды высотой h1. Даны диаметры: поршня D, штока d.
Весом поршня и штока пренебречь. Исходные данные приведены в таблице 2.140.
Задача 2-141
В сосуде, указанном на рисунке 2.118, находится расплавленный свинец (ρ = 11 г/см3). Определить силу давления, действующую на дно сосуда, если высота уровня свинца h, диаметр сосуда D, показание мановакуумметра pвак. Исходные данные приведены в таблице 2.141.
Задача 2-142
Определить давление p1 жидкости, которую необходимо подвести к гидроцилиндру (рис. 2.119), чтобы преодолеть усилие, направленное вдоль штока F. Даны диаметры: цилиндра — D, штока — d. Давление в бачке p0, высота H0. Силу трения не учитывать. Плотность жидкости ρ = 1000 кг/м3. Исходные данные приведены в таблице 2.142.
Задача 2-143
Определить давление p в верхнем цилиндре гидропреобразователя (мультипликатора), указанного на рисунке 2.120, если показание манометра, присоединенного к нижнему цилиндру, равно pм. Поршни перемещаются вверх, причем сила трения составляет 10% от силы давления жидкости на нижний поршень. Вес поршней G, а их диаметры D и d, высота H = 2,5 м. Плотность масла ρ = 900 кг/м3. Исходные данные приведены в таблице 2.143.
Задача 2-144
Определить показание мановакуумметра pмв, если к штоку поршня приложена сила F, его диаметр d, высота H, плотность жидкости ρ = 800 кг/м3 (рис. 2.121). Исходные данные приведены в таблице 2.144.
Задача 2-145
Определить силу, действующую на каждую из четырех стенок сосуда, имеющего форму перевернутой правильной треугольной пирамиды (рис. 2.122), если известны pм, H и h. Каждая сторона основания пирамиды b. Плотность жидкости ρ = 800 кг/м3. Исходные данные приведены в таблице 2.145.
Часть задач есть решенные, контакты
СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ
Задача 2-146
Определить величину и направление силы гидростатического давления воды на 1 м ширины нижней криволинейной части сооружения (рис. 2.126), если известны значения H и r. Исходные данные приведены в таблице 2.146.
Задача 2-147
Определить силу давления воды и точку приложения равнодействующей силы на круглый наклонный щит диаметром d (рис. 2.127), если известны и α.
Исходные данные приведены в таблице 2.147.
Задача 2-148
Определить суммарное давление воды на секторный затвор, закрывающий прямоугольное отверстие резервуара (рис. 2.128). Найти равнодействующую силу гидростатического давления на затвор. Исходные данные приведены в таблице 2.148.
Задача 2-149
Определить величину и направление равнодействующей силы давления воды на криволинейную стенку резервуара в виде четверти цилиндрической поверхности радиусом R и шириной b (рис. 2.129), если глубина воды в резервуаре H и давление на поверхности pм. Исходные данные приведены в таблице 2.149.
Задача 2-150
Определить величину и направление равнодействующей силы давления воды на секторный затвор, перекрывающий прямоугольное отверстие (рис. 2.130). Крышка имеет форму четверти кругового цилиндра. Глубина воды над затвором h, ширина затвора b и радиус кривизны затвора r. Исходные данные приведены в таблице 2.150.
Задача 2-151
Определить величину и направление равнодействующей силы давления воды на цилиндрический затвор плотины, перекрывающий прямоугольное донное отверстие высотой h, шириной b (рис. 2.131). Величина напора H. Исходные данные приведены в таблице 2.151.
Задача 2-152
Определить суммарную силу и направление равнодействующей силы давления воды на секторный затвор, закрывающий прямоугольное донное отверстие плотины, имеющее высоту r и ширину b (рис. 2.132), если напор плотины H. Исходные данные приведены в таблице 2.152.
Задача 2-153
Определить величину и направление равнодействующей силы давления воды на секторный затвор и точку ее приложения D (рис. 2.133) при следующих данных: радиус затвора R, ширина затвора b и угол α. Исходные данные приведены в таблице 2.153.
Задача 2-154
Определить величину суммарной силы давления воды F на секторный затвор радиусом R (рис. 2.134) при заданных значениях ширины затвора b (в направлении, перпендикулярном плоскости чертежа) и угла α. Построить эпюру гидростатического давления и найти точку приложения силы суммарного давления. Исходные данные приведены в таблице 2.154.
Задача 2-155
В призматическом сосуде шириной b (рис. 2.135) установлена перегородка, имеющая в своей нижней части форму четверти цилиндрической поверхности радиусом R. Определить суммарное давление воды на криволинейную часть перегородки, если глубина воды слева H1 и справа H2. Найти точку приложения равнодействующей силы давления воды. Исходные данные приведены в таблице 2.155.
Задача 2-156
Определить силу давления воды на затвор, расположенный в туннеле сечением h хм (рис. 2.136), а также найти угол β, под которым эта сила направлена относительно горизонта. Высота воды H, радиус r. Расчет вести на 1 погонный метр ширины затвора. Исходные данные приведены в таблице 2.156.
Задача 2-157
Определить величину и направление равнодействующей силы давления воды на криволинейную стенку AB резервуара (рис. 2.137) в виде четверти цилиндрической поверхности радиусом R и шириной b, если глубина воды в резервуаре H, давление на поверхности pм.
Исходные данные приведены в таблице 2.157.
Задача 2-158
В прямоугольном окне вертикальной стенки резервуара, представленного на рисунке 2.138, установлен на цапфах цилиндрический затвор диаметром d и шириной b. Определить суммарное усилие на затвор ABCD при напоре H. Исходные данные приведены в таблице 2.158.
Задача 2-159
В прямоугольном окне вертикальной стенки резервуара (рис. 2.139) установлен на цапфах цилиндрический затвор диаметром d, шириной b. Определить суммарное усилие на цапфах и момент от воздействия воды на затвор при напоре H. Исходные данные приведены в таблице 2.159.
Задача 2-160
Определить отрывающее усилие, воспринимаемое болтами полусферической крышки радиусом r (рис. 2.140), если показания манометра pм, глубина бензина h. Исходные данные приведены в таблице 2.160.
Задача 2-161
При испытании цилиндрического резервуара диаметром d1 на водонепроницаемость (рис. 2.141) к его полусферической крышке присоединена вертикальная трубка диаметром d2. Определить усилие, отрывающее крышку от резервуара и воспринимаемое болтами, если заданы высота h, удельный вес жидкости γ и масса крышки m. Исходные данные приведены в таблице 2.161.
Задача 2-162
Определить величину и направление равнодействующей силы давления воды на полуцилиндрическую поверхность диаметром d (рис. 2.142), если длина цилиндра по образующей . Напоры воды имеют значения h1 + d и h2 соответственно. Исходные данные приведены в таблице 2.162.
Задача 2-163
Определить силу, действующую на полусферическую крышку, закрывающую круглое отверстие в вертикальной стенке резервуара с нефтью (рис. 2.143). Исходные данные приведены в таблице 2.163.
Задача 2-164
В прямоугольном окне вертикальной стенки резервуара установлен на цапфах цилиндрический затвор диаметром d и шириной b (рис. 2.144). Определить величину и направление равнодействующей силы давления воды на затвор ABCD. Исходные данные приведены в таблице 2.164.
Задача 2-165
Определить величину, направление и точку приложения равнодействующей силы давления воды на цилиндрический затвор плотины, перекрывающей прямоугольное донное отверстие высотой h, шириной b (рис. 2.145). Глубина воды слева H1, справа H2. Исходные данные приведены в таблице 2.165.
Задача 2-166
Определить величину и направление силы давления на секторный затвор при расчете на 1 погонный метр ширины затвора, если известен напор H (рис. 2.146). Исходные данные задачи приведены в таблице 2.166.
Задача 2-167
Определить величину и направление равнодействующей силы двустороннего давления воды на полуцилиндрическую поверхность диаметром d (рис. 2.147), если длина цилиндра по образующей , глубина воды слева h1 = d, справа h2 = d/2. Исходные данные приведены в таблице 2.167.
Задача 2-168
Определить силу давления воды на секторный затвор (рис. 2.148), если известны значения Н, h, r, α. Найти также угол β, под которым направлена эта сила относительно горизонта при расчете на 1 погонный метр ширины затвора. Исходные данные приведены в таблице 2.168.
Задача 2-169
Определить величину и направление равнодействующей силы давления бензина на криволинейную стенку AB резервуара в виде четверти цилиндрической поверхности радиусом r, шириной b, если глубина в
резервуаре H, давление на поверхности pм (рис. 2.149). Исходные данные приведены в таблице 2.169.
Задача 2-170
Определить силу давления воды на стальной шар радиусом R (рис. 2.150), перекрывающий круглое отверстие в вертикальной стенке диаметром d = 1,5R. Исходные данные приведены в таблице 2.170.
Задача 2-171
Цилиндрический резервуар диаметром D имеет дно в виде полусферы (рис. 2.151). Высота верхней части резервуара h1, нижней — h2. Вычислить силу манометрического давления нефти на дно резервуара. Мысленно разрезав резервуар на две части, определить силу манометрического давления на половину боковой поверхности резервуара и найти точку приложения силы. Исходные данные приведены в таблице 2.171.
Задача 2-172
Определить силу давления воды на деталь, имеющую форму четверти круглого цилиндра радиусом r и укрепленную на болтах (рис. 2.152). Найти угол β, под которым направлена эта сила относительно горизонта. Расчет вести на единицу ширины конструкции. Напор воды H, радиус r. Исходные данные приведены в таблице 2.172.
Задача 2-173
Определить силу давления воды на криволинейную поверхность AB шириной b, радиусом r при известных h1, h2, α (рис. 2.153). Исходные данные приведены в таблице 2.173.
Задача 2-174
Определить величину и направление равнодействующей силы давления воды на цилиндрический затвор плотины, перекрывающий прямоугольное донное
отверстие высотой h, шириной b (рис. 2.154). Напор воды — H. Исходные данные приведены в таблице 2.174.
Задача 2-175
Определить растягивающее и срезающее усилия, действующие на болты, которыми прикреплена полусферическая крышка, закрывающая круглое отверстие в вертикальной стенке резервуара с водой (рис. 2.155).
Исходные данные приведены в таблице 2.175.
Задача 2-176
Вертикальный цилиндрический резервуар для хранения мазута (γм = 8340 Н/м3) диаметром d1 имеет полусферическую крышку массой m и сообщается с атмосферой через трубу диаметром d2 (рис. 2.156). Определить высоту h, если усилие, отрывающее крышку от резервуара, F. Исходные данные приведены в таблице 2.176.
Задача 2-177
Определить силы давления, приложенные к плоской (А) и полусферической (В) торцевым стенкам горизонтального цилиндра, плунжер которого нагружен силой F при известных R и d.
Задачи 2-178
Металлическая цистерна, имеющая диаметр d и длину , полностью заполнена минеральным маслом ρм.м = 0,9 · 103 кг/м3 (рис. 2.158). Давление на поверхность цистерны равно атмосферному. Определить силу давления масла на левую внутреннюю криволинейную поверхность. Исходные данные приведены в таблице 2.178.
Задачи 2-179-2-189
Определить равнодействующую силу избыточного давления на 1 погонный метр длины (нормально к площади чертежа) поверхности АВС. Найти угол наклона линии действия силы избыточного давления воды на поверхность АВС. Построить эпюры горизонтального, вертикального и нормального избыточного давления на поверхность АВС при данных, приведенных на рисунках 2.159-2.169. Исходные данные к задачам приведены в таблице 2.179.
Задача 2-190
Определить величину и направление силы гидростатического давления воды на 1 м ширины вальцового затвора диаметром D (рис. 2.170). Исходные данные приведены в таблице 2.180.
Задача 2-191
Определить силу гидростатического давления воды на 1 м ширины вальцового затвора диаметром d (рис. 2.171) при известных h1 и h2. Исходные данные приведены в таблице 2.181.
Задача 2-192
Определить силу давления на 1 м ширины затвора, перекрывающего канал между двумя смежными камерами (рис. 2.172), если глубина воды в левой камере h1, в правой — h2, а также известны значения R, a, α, β. Исходные данные приведены в таблице 2.182.
Задача 2-193
Цилиндр радиусом r и длиной перекрывает отверстие в дне резервуара размерами a х (рис. 2.173). Определить: а) силу давления воды на цилиндр при известных H и p0 = pатм; б) при какой глубине H цилиндр всплывет, если его вес G = 20 кг, а давление на поверхности p0. Исходные данные приведены в таблице 2.183.
Задача 2-194
Круглое отверстие в вертикальной стенке закрытого резервуара с водой перекрыто сферической крышкой (рис. 2.174). Радиус сферы R, угол α, глубина погружения центра тяжести отверстия H. Определить силу давления жидкости Fм на крышку при манометрическом давлении на свободной поверхности жидкости pм. Исходные данные приведены в таблице 2.184.
Задача 2-195
Стальная труба диаметром D работает под давлением p. Найти: а) необходимую толщину стенок трубы, если допустимое напряжение для стали [σ] = 150 · 103 МПа; б) максимальное допустимое напряжение при толщине стенки трубы δ. Исходные данные приведены в таблице 2.185.
Задача 2-196
Определить величину и направление силы давления воды на 1 м ширины затвора, представляющего собой четверть кругового цилиндра радиуса R (рис. 2.175). Исходные данные приведены в таблице 2.186.
Задача 2-197
Определить величину и направление силы давления воды на 1 м ширины затвора (рис. 2.176), если известны R и H. Исходные данные приведены в таблице 2.187.
Задача 2-198
Определить величину и направление силы давления воды на 1 м ширины щита (рис. 2.177), если известны R, α, β. Исходные данные приведены в таблице 2.188.
Задача 2-199
Определить величину и направление силы давления воды на 1 м ширины секторного затвора радиуса R при известной величине β (рис. 2.178). Исходные данные приведены в таблице 2.189.
Задача 2-200
Изогнутая труба диаметром D находится под давлением p (рис. 2.179). Определить силу давления воды на колено, а также отрывающие и сдвигающие усилия, которые возникают на стыках колена с прямолинейным участком трубы, если угол поворота трубы α. Исходные данные приведены в таблице 2.190.
Задача 2-201
Определить величину и направление силы давления воды на цилиндрический затвор диаметром D и длиной Z (рис. 2.180), перегораживающий прямоугольный канал шириной b, если глубина воды с одной стороны щита H1, с другой — H2. Исходные данные приведены в таблице 2.191.
Задача 2-202
Определить отрывающее усилие, воспринимаемое болтами полусферической крышки диаметром d (рис. 2.181), если показание манометра p0, а глубина воды h. Как изменится усилие, если крышка будет плоской? Исходные данные приведены в таблице 2.192.
Задача 2-203
По стальному трубопроводу диаметром d подается вода под давлением p (рис. 2.182). Определить напряжение в стенке трубопровода, если толщина ее δст. Исходные данные приведены в таблице 2.193.
Задача 2-204
Деревянная бочка диаметром d и высотой h, указанная на рисунке 2.183, стянута двумя стальными обручами сечением 50 х 3 мм2. В верхнее днище вставлена труба, в которую налита вода на высоту h1. Определить напряжение материала в верхнем и нижнем обручах. Исходные данные к задаче приведены в таблице 2.194.
Часть задач есть решенные, контакты
ПЛАВАНИЕ ТЕЛ
Задача 2-205
Автомобиль весом Ga установлен на паром размерами Z×В×Н (рис. 2.185). Проверить остойчивость парома, если его вес Gп приложен на половине его высоты, а центр тяжести автомобиля находится на высоте hа от верхней плоскости парома. Установить, как изменится метацентрическая высота hм, если на автомобиль будет уложен груз Gг, центр тяжести которого расположен на высоте hг от верхней плоскости парома Исходные данные к задаче приведены в таблице 2.195.
Задача 2-206
Цилиндр диаметром D и высотой H, изготовленный из дерева (ρ = 800 кг/м3), плавает в воде таким образом, что его ось направлена вертикально. Требуется: а) проверить остойчивость цилиндра; б) найти высоту цилиндра H, при которой он начинает терять остойчивость. Исходные данные к задаче приведены в таблице 2.196.
Задача 2-207
Плавучий железобетонный тоннель с наружным диаметром D и толщиной стенок δ удерживается от всплытия тросами, расположенными попарно через каждые метров длины тоннеля (рис. 2.186). Определить натяжение тросов, если вес одного метра дополнительной нагрузки по длине равен q, плотность бетона ρб = 2450 кг/м3 и угол α. Как изменится натяжение тросов при уменьшении наружного диаметра тоннеля на 1 м? Исходные данные к задаче приведены в таблице 2.197.
Задача 2-208
Длина прямоугольного понтона Z, ширина B, высота H. Вес понтона Gп. Проверить понтон на остойчивость без нагрузки и при максимальной нагрузке G, при которой высота бортов над ватерлинией равна .
Центр тяжести понтона и дополнительной нагрузки расположен на расстоянии h от дна. Исходные данные к задаче приведены в таблице 2.198.
Задача 2-209
Для перевозки автомобилей весом до Gа через реку сооружается плот из бревен диаметром d и длиной l. Определить, сколько бревен нужно для сооружения плота, способного удержать еще и груз G, если плотность дерева ρд = 800 кг/м3. Будет ли плот остойчив, если все бревна уложить вплотную, поровну в каждом из двух рядов, а центр тяжести автомобиля расположен на высоте h над верхней плоскостью плота? Исходные данные приведены в таблице 2.199.
Задача 2-210
Объемное измещение подводной лодки V. С целью погружения подводной лодки отсеки были заполнены морской водой в количестве V1. Относительный удельный вес морской воды 1,025. Определить: а) какая часть подводной лодки (в %) будет погружена в воду, если из подводной лодки удалить всю воду и она всплывет; б) чему равен вес подводной лодки без воды. Исходные данные к задаче приведены в таблице 2.200.
Задача 2-211
Определить количество бревен n, из которых нужно сколотить плот, чтобы перевезти груз весом G1. Диаметр бревен d1, длина l. Глубина погружения бревен y. Масса перевозчика m. Относительный удельный вес намокших бревен 0,75. Какое количество бревен понадобится, если верх плота будет заподлицо со свободной поверхностью? Исходные данные к задаче приведены в таблице 2.201.
Задача 2-212
По окончании погрузки V (м3) песка осадка баржи увеличилась на h. Определить плотность песка, если площадь плоскости плавания баржи F и величину изменения осадки баржи, если вместо песка на баржу будет погружено Vк (м3) извести плотностью ρ = 800 (кг/м3). Исходные данные к задаче приведены в таблице 2.202.
Задача 2-213
Прямоугольная деревянная шаланда весом G и длиной L должна иметь полезное водоизмещение P. Определить необходимую ширину шаланды B и высоту ее бортов H при условии, что метацентрическая высота hм, высота бортов нагруженной шаланды над ватерлинией h, а центр тяжести ее совпадает с центром тяжести поперечного сечения. Как необходимо изменить ширину шаланды B и высоту ее бортов H, чтобы ее полное водоизмещение стало равным P1? Исходные данные к задаче приведены в таблице 2.203.
Задача 2-214
Прямоугольный деревянный брус длиной, шириной b, высотой h с удельным весом γд = 0,75 т/м3 плавает в воде (рис. 2.187). Определить остойчивость бруса в двух положениях. При каком соотношении b/h брус еще будет остойчивым? Исходные данные к задаче приведены в таблице 2.204.
Задача 2-215
Во избежание переполнения водой резервуар снабжен поплавковым клапаном диаметром d (рис. 2.188). При каком уровне воды в резервуаре клапан откроется, если длина тяги клапана и вес поплавка с клапаном составляет соответственно l и G? Исходные данные к задаче приведены в таблице 2.205.
Задача 2-216
В цилиндрическом сосуде (рис. 2.189) плавает кусок льда относительного удельного веса δ1 = 0,9, в котором находится стальной шарик, относительный удельный вес которого δ2 = 7,8. Объем льда V1, объем шарика V2. Определить: а) какая часть суммарного объема льда находится над водой; б) как изменится уровень Н в сосуде, когда лед растает, если диаметр сосуда D. Исходные данные к задаче приведены в таблице 2.206.
Задача 2-217
Дюкер, выполненный из стальных труб диаметром d, должен опускаться на дно реки без заполнения водой. Определить необходимый объем V бетонного балласта на 1 пог. м для обеспечения погружения трубопровода, если плотность бетона ρб = 2500 кг/м3. Коэффициент запаса от всплытия k. Исходные данные к задаче приведены в таблице 2.207.
Часть задач есть решенные, контакты
3. ГИДРОДИНАМИКА
УРАВНЕНИЕ БЕРНУЛЛИ. БЕЗ УЧЕТА ПОТЕРЬ НАПОРА (ЭНЕРГИИ)
Задача 3-1
Приемник воздушных давлений самолета показывает разность уровней рабочей жидкости h (рис. 3.4). Определить скорость самолета на высоте H (при решении использовать стандартную атмосферу). Исходные данные приведены в таблице 3.1.
Задача 3-2
Под действием разности уровней H и при избыточном давлении p0 по трубе переменного сечения вода перетекает из верхнего резервуара в нижний (рис. 3.5). Определить расход воды и построить пьезометрическую линию без учета потерь на трение, если известны диаметры d1, d2 = d1/2, d3 = d1/3. Исходные данные приведены в таблице 3.2.
Задача 3-3
Определить теоретический расход воды в водомере Вентури, установленном под углом α к горизонту (рис. 3.6), если разность уровней, показываемая дифференциальным ртутным манометром, равна h. Диаметр большого и малого сечений равны соответственно D и d, расстояние между сечениями l. Исходные данные приведены в таблице 3.3.
Задача 3-4
Определить избыточное давление воды на входе в брандспойт и диаметр выходного сечения d, необходимые для получения струи мощностью Q, бьющей вертикально вверх на высоту H при диаметре входного сечения D = 60 мм. Потери не учитывать. Исходные данные приведены в таблице 3.4.
Задача 3-5
Определить, при каком напоре H1 разрежение в узком сечении трубы станет pв = 0,2 атм (рис. 3.7). Найти также расход жидкости через трубу. Построить пьезометрическую линию, если известны d1, d2, d3, H2 = 1,5 м. Потери на трение не учитывать. Исходные данные приведены в таблице 3.5.
Задача 3-6
Определить необходимый диаметр трубы и разряжение в верхней точке сифона при заданных H и Z, а также расход воды Q (рис. 3.8). Потерями напора на трение пренебречь. Исходные данные приведены в таблице 3.6.
Задача 3-7
Какую разность уровней h покажет дифференциальный манометр, заполненный водой при расходе воздуха Q (γв = 1,2 кг/м3) через горизонтальную трубу Вентури. Диаметры D и d известны, потерями пренебречь.
Задача 3-8
Дифференциальный ртутный манометр имеет показания H (рис. 3.10). Определить расход воды в трубе переменного сечения с диаметрами d1 и d2. Исходные данные приведены в таблице 3.8.
Задача 3-9
По трубопроводу переменного сечения протекает вода с расходом Q, диаметр суженной части d2 (рис. 3.11). Определить диаметр основного трубопровода d1, если разность показаний пьезометров hр. Исходные данные приведены в таблице 3.9.
Задача 3-10
Определить высоту подъема жидкости в первом пьезометре h1, если высота подъема во втором h2 при известных d1, d2, Q (рис. 3.11). Исходные данные приведены в таблице 3.10.
Задача 3-11
Определить расход воды Q в трубопроводе переменного сечения, если известны диаметры d1, d2, разность показаний пьезометров hр (рис. 3.11). Исходные данные приведены в таблице 3.11.
Задача 3-12
По трубопроводу переменного сечения протекает вода с расходом Q, диаметр суженной части трубопровода d2. Определить разность показаний пьезометра hр, если диаметр главного трубопровода d1 (рис. 3.11). Исходные данные приведены в таблице 3.12.
Задача 3-13
На водопроводной трубе диаметром d1 установлен водомер Вентури диаметром d2 (рис. 3.12). Определить расход воды Q, протекающей по трубе, если разность уровней в пьезометрах hр. Исходные данные приведены в таблице 3.13.
Задача 3-14
Определить разность уровней воды в пьезометре hр при известных значениях d1, d2 и Q (рис. 3.12). Исходные данные приведены в таблице 3.14.
Задача 3-15
На водопроводной трубе диаметром d1 установлен водомер Вентури, имеющий диаметр узкой части d2. Определить величину расхода Q (рис. 3.12). Исходные данные приведены в таблице 3.15.
Задача 3-16
Пренебрегая потерями напора, определить давление p2, если по трубе протекает бензин, при известных значениях d1, d2, Q, p1/γ (рис. 3.12). Исходные данные приведены в таблице 3.16.
Задача 3-17
На водопроводной трубе установлен водомер Вентури, имеющий диаметр узкой части d2 (рис. 3.12). Определить диаметр d1 при известном расходе Q. Исходные данные приведены в таблице 3.17.
Задача 3-18
На водопроводной трубе диаметром d1, пропускающей воду с расходом Q, установлен водомер Вентури (рис. 3.12). Определить диаметр узкой части водомера d2. Исходные данные приведены в таблице 3.18.
Задача 3-19
Определить диаметр трубопровода d1, если известны hр, d2, Q (рис. 3.13). Исходные данные приведены в таблице 3.19.
Задача 3-20
К трубопроводу переменного сечения присоединены два пьезометра (рис. 3.13). Определить диаметр трубы d2, если известны h1, h2, d1, Q. Исходные данные приведены в таблице 3.20.
Задача 3-21
Пренебрегая потерями напора, определить расход протекающего по трубопроводу керосина, если разность уровней в пьезометрах hр и диаметры d1 и d2 (рис. 3.13). Исходные данные приведены в таблице 3.21.
Задача 3-22
К трубопроводу переменного сечения присоединены два пьезометра (рис. 3.13). Определить, на какую высоту h1 поднимается вода в первом пьезометре, если известны высота воды во втором пьезометре h2, диаметры d1, d2 и расход Q. Исходные данные приведены в таблице 3.22.
Задача 3-23
Определить расход воды в трубе и критическую скорость υкр перехода ламинарного режима в турбулентный, если известны напор Н и диаметр d (рис. 3.14). Исходные данные приведены в таблице 3.23.
Задача 3-24
Определить число Рейнольдса и режим движения жидкости в водопроводной трубе диаметром d, если расход протекающей по ней воды Q, температура воды T (рис. 3.14). Найти критическую скорость. Исходные данные приведены в таблице 3.24.
Задача 3-25
Определить расход нефти, протекающей по трубопроводу, имеющему сужение, если известны диаметры d1 и d2, разность уровней в ртутном дифференциальном пьезометре Δh (рис. 3.15). Исходные данные приведены в таблице 3.25.
Задача 3-26
Определить абсолютное давление воды в сечении диаметром d1, если известны Q, h, d1, d2.
Задача 3-27
Зная высоту h подъема воды в узкой части трубопровода, диаметр d2 и давление p1 в сечении 1–1, определить диаметр d1, если известен расход Q.
Задача 3-28
По трубопроводу, имеющему сужение, протекает вода с расходом Q (рис. 3.16). Определить, какой диаметр d2 должна иметь узкая часть трубопровода, чтобы обеспечивать засасывание воды из резервуара на высоту h, если известны d1 и p1. Исходные данные приведены в таблице 3.28.
Задача 3-29
Определить, на какую высоту h может засасываться вода из резервуара по трубке, присоединенной к узкому сечению трубопровода, при расходе Q, диаметрах d1, d2 и давлении p1 (рис. 3.16). Исходные данные приведены в таблице 3.29.
Задача 3-30
Определить расход жидкости Q, протекающей по трубопроводу, имеющему сужение, если известны d1, d2, h, p1 (рис. 3.16). Исходные данные приведены в таблице 3.30.
Задача 3-31
По трубопроводу, имеющему сужение, протекает вода с расходом Q (рис. 3.17). Определить диаметр d2 узкой части трубопровода, если известны d1, h1, h2. Исходные данные приведены в таблице 3.31.
Задача 3-32
По трубопроводу, имеющему сужение, протекает вода с расходом Q (рис. 3.17). Определить диаметр d1 трубопровода, если известны h1, h2, d2. Исходные данные приведены в таблице 3.32.
Задача 3-33
Определить расход жидкости Q, протекающей по трубопроводу, имеющему сужение, если известны hр, d1, d2 (рис. 3.17). Исходные данные приведены в таблице 3.33.
Задача 3-34
На водопроводной трубе диаметром d1 установлен водомер диаметром d2 (рис. 3.17). На какую высоту h2 поднимается вода в пьезометрической трубке, присоединенной к узкому сечению, при пропуске расхода Q, если уровень воды в пьезометре, присоединенном к трубе, h1? Исходные данные приведены в таблице 3.34.
Задача 3-35
На водопроводной трубе диаметром d1 установлен водомер диаметром d2 (рис. 3.17). На какую высоту h1 поднимается вода в трубе при пропуске расхода Q, если уровень воды в пьезометре, присоединенном к узкому сечению, h2? Исходные данные приведены в таблице 3.35.
Задача 3-36
На водопроводной трубе, имеющей сужение, определить разность уровней в пьезометрах hр, если известны расход Q, d1 и d2 (рис. 3.17). Исходные данные приведены в таблице 3.36.
Задача 3-37
Определить расход воды Q, протекающей по горизонтальному трубопроводу, имеющему сужение, если известны d1, d2, h1 и h2 (рис. 3.18). Исходные данные приведены в таблице 3.37.
Задача 3-38
По горизонтальному трубопроводу подается бензин (рис. 3.18). Определить разность уровней в пьезометрах hр, если известны d1, d2 и Q. Исходные данные приведены в таблице 3.38.
Задача 3-39
Определить высоту засасывания воды из резервуара, если известны d1, d2, h1 и расход Q (рис. 3.19). Исходные данные приведены в таблице 3.39.
Задача 3-40
Определить расход трубопровода Q, если диаметр узкого сечения d2, высота засасывания воды из резервуара h, диаметр трубопровода d1, избыточное давление p1 (рис. 3.19). Исходные данные приведены в таблице 3.40.
Задача 3-41
По трубопроводам A и B одинакового диаметра d подается под давлением вода (рис. 3.20). К трубопроводам присоединен пьезометр для измерения разности давления в трубах. Определить скорость движения воды в трубопроводах и расход QA в трубопроводе A, если удельные энергии в трубопроводах A и B равны. Показание ртутного пьезометра Z. Расход воды в трубопроводе B составляет QB. Исходные данные приведены в таблице 3.41.
Задача 3-42
Разность давлений в сечениях 1 – 1 и 2 – 2 трубчатого расходомера с диаметрами D и d составляет Δp (рис. 3.21). Определить расход воды, если: а) ось расходомера горизонтальна; б) ось расходомера наклонна и точка A в сечении 1 – 1 ниже точки B в сечении 2 – 2 на величину ΔZ. Исходные данные приведены в таблице 3.42.
Задача 3-43
Из резервуара по трубопроводу, имеющему сужение, вытекает вода (рис. 3.22). Определить диаметр d суженной части трубопровода, при котором давление в этом сечении будет p, если напор H, а диаметр D. Исходные данные приведены в таблице 3.43.
Задача 3-44
Из резервуара по трубопроводу, имеющему сужение, вытекает вода (рис. 3.22). Определить напор H, при котором давление в суженной части трубопровода p, если диаметры D и d. Исходные данные приведены в таблице 3.44.
Задача 3-45
Из резервуара по трубопроводу, имеющему сужение, вытекает вода (рис. 3.22). Определить, на какую высоту h поднимется вода в трубке, присоединенной к суженной части трубопровода, если напор H и диаметры D и d. Исходные данные приведены в таблице 3.45.
Задача 3-46
Из открытого резервуара A по вертикальной трубе диаметром d вода перетекает в нижний закрытый резервуар B при напоре H (рис. 3.23). Определить расход воды в трубе, если показание ртутного манометра, установленного на нижнем резервуаре, h. Исходные данные приведены в таблице 3.46.
Задача 3-47
Из открытого резервуара A по вертикальной трубе диаметром d вода перетекает в нижний закрытый резервуар B при напоре H (см. рис. 3.23). Определить показание h ртутного манометра, установленного на нижнем резервуаре, при расходе воды в трубе Q. Исходные данные приведены в таблице 3.47.
Задача 3-48
Из открытого резервуара вода вытекает по расширяющейся трубе диаметрами d1 и d2, длиной от суженой части до выходного сечения H2 (рис. 3.24). Найти, при каком напоре H1 в верхнем резервуаре полное давление в суженной части трубы станет равным p. Исходные данные приведены в таблице 3.48.
Задача 3-49
Из открытого резервуара вода вытекает по расширяющейся трубе диаметрами d1 и d2, длиной от суженой части до выходного сечения H2 (рис. 3.24). Найти полное давление в суженной части трубы при напоре H1. Исходные данные приведены в таблице 3.49.
Задача 3-50
Вода вытекает в атмосферу из закрытого резервуара, имеющего ртутный манометр, по трубе переменного сечения с диаметрами d1 и d2 при напоре H (рис. 3.25). Построить пьезометрическую линию и определить расход воды в трубе при показании ртутного манометра . Исходные данные приведены в таблице 3.50.
Задача 3-51
Вода вытекает в атмосферу из закрытого резервуара, имеющего ртутный манометр, по трубе переменного сечения с диаметрами d1 и d2 при напоре H (рис. 3.25). Построить пьезометрическую линию и определить показание ртутного манометра при расходе воды Q. Исходные данные приведены в таблице 3.51.
Задача 3-52
Из открытого резервуара по сифонному трубопроводу вытекает вода (рис. 3.26). Определить, при каком расстоянии Z1 между уровнем воды в резервуаре и выходом из трубы и при каком расходе давление в сечении x – x достигнет значения pX, если ось трубы в сечении x – x выше уровня воды в резервуаре на величину Z2, а диаметр трубопровода d. Исходные данные приведены в таблице 3.52.
Задача 3-52
Из открытого резервуара по сифонному трубопроводу вытекает вода (рис. 3.26). Определить, при каком расстоянии Z1 между уровнем воды в резервуаре и выходом из трубы и при каком расходе давление в сечении x – x достигнет значения pX, если ось трубы в сечении x – x выше уровня воды в резервуаре на величину Z2, а диаметр трубопровода d. Исходные данные приведены в таблице 3.52.
Задача 3-53
Из открытого резервуара по сифонному трубопроводу вытекает вода (рис. 3.26). Определить давление pX в сечении x – x и диаметр трубопровода при заданных значениях Q, Z1 и Z2. Исходные данные приведены в таблице 3.53.
Задача 3-54
Определить расход воды в трубопроводе и скорости в сечениях, если диаметр трубопровода d1 уменьшается до величины d2, а показание пьезометра, подсоединенного к сечениям 1 – 1 и 2 – 2, равно h (рис. 3.27). Высотой столба воздуха в пьезометре пренебречь. Исходные данные приведены в таблице 3.54.
Задача 3-55
Вода течет по трубопроводу диаметром d со скоростью υ (рис. 3.28). Внизу вода растекается во все стороны радиально между двумя круглыми параллельными пластинами диаметром D, расположенными на расстоянии a друг от друга. Определить давление в точках A и B, отстоящих на расстояние D/4 от центра трубы. Вода вытекает в атмосферу. Исходные данные приведены в таблице 3.55.
Задача 3-56
Из бачка A по трубке диаметром d3, подведенной к трубопроводу диаметром d2, поступает хлорная вода плотностью ρ = 1000 кг/м3 (рис. 3.29). Определить расход хлорной воды в трубке диаметром d3, если напор H, диаметр в широкой части d1, давление в сечении 1 – 1 равно p, а расход воды в трубопроводе переменного сечения Q. Исходные данные приведены в таблице 3.56.
Задача 3-57
Из резервуара вода вытекает через трубку переменного сечения с небольшим углом конусности и диаметрами d1 и d2 (рис. 3.30). Определить напор H, при котором давление в трубке в сечении диаметром d1 станет p1, если давление на поверхности воды в резервуаре равно атмосферному. Исходные данные приведены в таблице 3.57.
Задача 3-58
Из резервуара вода вытекает через трубку переменного сечения с небольшим углом конусности и диаметрами d1 и d2 (рис. 3.30). Определить давление на поверхность воды в резервуаре p0, при котором давление в трубке в сечении диаметром d1 станет p2, если напор равен H1. Исходные данные приведены в таблице 3.58.
Задача 3-59
Насос производительностью Q забирает воду из колодца по трубе диаметром d (рис. 3.31). Определить наибольший вакуум pвак в трубе при высоте установки насоса h. Исходные данные приведены в таблице 3.59.
Задача 3-60
Насос производительностью Q забирает воду из колодца по трубе диаметром d (рис. 3.31). Определить высоту установки насоса h при условии, что наибольший вакуум в трубе не превышает pвак. Исходные данные приведены в таблице 3.60.
Задача 3-61
Жидкость вытекает из открытого резервуара в атмосферу через трубу, имеющую плавное сужение до диаметра d1, а затем постепенное расширение до d2 (рис. 3.32). Истечение происходит под действием напора H. Пренебрегая потерями энергии, определить абсолютное давление в узком сечении трубы 1 – 1, если соотношение диаметров d2/d1 =, атмосферное давление соответствует hа = 750 мм рт. ст. Плотность жидкости ρ = 1000 кг/м3.
Найти напор Hкр, при котором абсолютное давление в сечении 1 – 1 будет равным нулю. Исходные данные приведены в таблице 3.61.
Задача 3-62
Пренебрегая потерями напора, определить степень расширения диффузора n = (D/d)2, при котором давление в сечении 2 – 2 возрастет в два раза по сравнению с давлением в сечении 1 – 1 (рис. 3.33). Расчет провести при следующих данных: известны расход жидкости Q, диаметр d, давление в сечении 1 – 1 p1, плотность жидкости ρ = 1000 кг/м3, режим течения принять: а) ламинарным и б) турбулентным. Поток в диффузоре считать стабилизированным и безотрывным. Исходные данные приведены в таблице 3.62.
Задача 3-63
По длинной трубе, указанной на рисунке 3.34, диаметром d протекает жидкость (ν = 2 Ст; ρ = 900 кг/м3). Определить расход жидкости и давление в сечении, где установлены пьезометр и трубка Пито, если известна разность H – h. Исходные данные приведены в таблице 3.63.
Задача 3-64
Вода течет по трубе диаметром D, имеющей отвод диаметром d (рис. 3.35). Пренебрегая потерями напора, определить расход жидкости в отводе Q‘, если расход в основной трубе Q, известны высоты Н и h. Режим течения считать турбулентным. Указание: считать, что давление перед отводом расходуется на создание скоростного напора в отводе и подъем жидкости на высоту h. Исходные данные приведены в таблице 3.64.
Задача 3-65
Жидкость плотностью ρ = 1000 кг/м3 протекает по металлической трубе диаметром dтр, а затем по резиновому шлангу, который имеет начальный диаметр dшл (рис. 3.36). Под действием давления жидкости p2 резиновый шланг растягивается до диаметра D. Жесткость шланга на диаметральное растяжение c = p2πDΔ/δ= 3 · 106 Н/м, где δ — приращение диаметра шланга Δ = 1,0 м. Определить диаметр шланга D, если известны давление p1 и расход жидкости Q. Указание: задачу решить методом последовательных приближений, задаваясь величиной D. Потерями пренебречь. Исходные данные приведены в таблице 3.65.
Часть задач есть решенные, контакты
УРАВНЕНИЕ БЕРНУЛЛИ С УЧЕТОМ ПОТЕРЬ НАПОРА. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ
Задача 3-66
Определить потери напора при внезапном расширении стальной трубы диаметром до расширения D1 при расходе Q и диаметром после расширения D2, если по трубе движется масло (рис. 3.46). Исходные данные приведены в таблице 3.66.
Задача 3-67
Из резервуара при постоянном манометрическом давлении pм = 20 кПа и постоянном уровне вытекает вода по вертикальной трубе переменного сечения, нижний конец которой погружен в открытый резервуар (рис. 3.47). Определить при H = 1,0 м расход воды Q в трубе и полное давление p2 в сечении 2 – 2, расположенном на высоте h = 0,5 м от свободной поверхности воды в нижнем резервуаре, если заданы d1 и d2. Указание: при решении задачи учитывать потери энергии только на преодоление местных сопротивлений. Исходные данные приведены в таблице 3.67.
Задача 3-68
На горизонтальном трубопроводе длиной 50 м установили дифференциальный пьезометр, разность уровней ртути в котором равна h (рис. 3.48). Используя показания пьезометра, определить коэффициент Дарси. Вычислить гидравлический уклон, если известны d1 и расход Q = 8 л/с. Исходные данные приведены в таблице 3.68.
Задача 3-69
Определить угол открытия крана, который обеспечил бы пропуск воды расходом Q по трубопроводу, если известны длина и диаметр трубопровода, а также напор H = 6 м и величина Z = H/4 (рис. 3.49). Исходные данные приведены в таблице 3.69.
Задача 3-70
Из резервуара вытекает вода по трубопроводу переменного сечения с диаметрами d1, d2, d3 при уровне воды над осью входа в трубу H. Длина участков трубопроводов l1, l2, l3. Определить скорость движения воды в выходном сечении трубопровода и построить пьезометрическую линию.
Задача 3-71
Всасывающая труба вентилятора имеет диаметр d и длину , коэффициент Дарси λ = 0,02, коэффициент потерь на плавном входе ζвх = 0,35 (рис. 3.51). Температура на улице Тв. Определить разряжение рвак = 20 кг/м2 перед вентилятором при производительности Q1 = 1300 м3/ч. Исходные данные приведены в таблице 3.71.
Задача 3-72
Всасывающая труба вентилятора имеет диаметр d и длину , коэффициент Дарси λ = 0,02, коэффициент потерь на плавном входе ζвх = 0,35 (рис. 3.51). Температура на улице TвºC. Определить производительность Q при заданном pвак. Исходные данные приведены в таблице 3.72.
Задача 3-73
Вода протекает из закрытого резервуара А в открытый В по трубе диаметром d и длиной l. Определить расход воды, если избыточное давление в сосуде А – рм, коэффициент местных сопротивлений вентиля ζв = 4; длина трубы l = H2 + 1 м, напоры H1 иH2, трубы стальные цельнотянутые, новые.
Задача 3-74
Лабиринтное уплотнение турбины расположено на диаметре D = 1 м и работает с перепадом давления Δp = p1 – p2 (рис. 3.53). Определить расход масла через уплотнение (γм = 880 кг/м3; υ = 0,1 см2/с), если известны зазор δ и длины участков . Исходные данные приведены в таблице 3.74.
Задача 3-75
При проведении опытов со стальной трубой диаметром d установлено, что закон гидравлического сопротивления соответствует квадратичной зоне, а коэффициент Дарси λ = 0,035. Определить эквивалентную шероховатость трубы. Исходные данные приведены в таблице 3.75.
Задача 3-76
В закрытом резервуаре поддерживается постоянное манометрическое давление рм, под действием которого по новой стальной трубе диаметром d и длинами l1, l2 и l3 вытекает вода при температуре T°.
Определить расход воды в трубе Q. Исходные данные приведены в таблице.
Задача 3-77
В закрытом резервуаре поддерживается постоянное манометрическое давление рм, под действием которого по новой стальной трубе диаметром d и длинами l1, l2 и l3 вытекает вода при температуре t°. Определить давление p в трубе в сечении 0–0, совпадающем со свободной поверхностью воды в резервуаре, если расход Q1.
Задача 3-78
Из открытого резервуара по сифонному трубопроводу вытекает вода с расходом Q (рис. 3.55). При заданных расстояниях Z1 и Z2 и длине трубопровода расстояние от начала трубопровода до сечения X – X составляет x, а коэффициент трения λ = 0,03. Определить диаметр трубопровода. Исходные данные приведены в таблице 3.78.
Задача 3-79
Из открытого резервуара по сифонному трубопроводу вытекает вода с расходом Q (рис. 3.55). При заданных расстояниях Z1 и Z2 и длине трубопровода l расстояние от начала трубопровода до сечения X–X составляет lx, а коэффициент трения λ = 0,03. Определить давление px в сечении X–X, если диаметр трубопровода d = 125 мм. Исходные данные приведены в таблице 3.79.
Задача 3-80
По трубопроводу диаметром d1, который внезапно суживается до d2, подается масло (ρм = 750 кг/м3). Давление в сечении с диаметром d1 составляет p1, а в сечении с d2 – p2. Геометрическая высота первого сечения над плоскостью сравнения, проходящей через центр тяжести второго сечения, равна z. Расход масла в трубе Q. Определить потери напора на рассматриваемом участке и вычислить гидродинамический напор в первом сечении.
Задача 3-81
Определить манометрическое давление, которое должен создавать насос, чтобы подать воду в количестве Q в водонапорный бак на высоту h по трубопроводу длиной (рис. 3.56). Диаметр трубы — d. Трубы нормальные, бывшие в эксплуатации; температура воды TºC, коэффициент сопротивления закругления ζз = 0,29. Исходные данные приведены в таблице 3.81.
Задача 3-82
На берегу реки предполагается устроить насосную станцию для подачи воды из реки Q. Высота оси насоса над уровнем воды в реке hн. Длина всасывающей трубы l, трубы чугунные, новые. Определить величину наибольшего вакуума. Исходные данные приведены в таблице.
Задача 3-83
На берегу реки предлагается устроить насосную станцию для подачи воды из реки Q (см. рис. 3.57). Высота оси насоса под уровнем воды в реке hн. Длина всасывающей трубы, трубы чугунные, новые. Определить величину наибольшего вакуума. Исходные данные приведены в таблице 3.83.
Задача 3-84
На берегу реки предлагается устроить насосную станцию для подачи воды из реки Q (см. рис. 3.57). Высота оси насоса под уровнем воды в реке hн. Длина всасывающей трубы , трубы чугунные, новые. Вычислениями доказать, будет ли вакуум в сечении 1 – 1, расположенном на глубине h1. Температуры воды TºC. Для определения ζзакр значение r/Rзак принять равным 0,45. Исходные данные приведены в таблице 3.84.
Задача 3-85
Для условия задачи 3.84 при заданных Q, d, определить высоту расположения оси насоса над уровнем воды (см. рис. 3.57). Вакуум во всасывающей трубе не должен превосходить hв. Трубы чугунные, нормальные. Исходные данные приведены в таблице 3.85.
Задача 3-86
Давление в трубопроводе диаметром d при закрытом кране равно p. Определить расход воды в трубопроводе, если при открытом кране давление в нем изменилось до p1.
Задача 3-87
Давление в трубопроводе диаметром d при закрытом кране равно p. Определить давление в кране при расходе в трубопроводе Q. Исходные данные приведены в таблице 3.87.
Задача 3-88
Из резервуара вытекает вода по трубопроводу переменного сечения с диаметрами d1, d2, d3 при напоре воды над осью входа в трубу H (рис. 3.58). Длины участков трубопровода соответственно 1, 2, 3. Построить пьезометрическую линию и определить скорость движения воды в выходном сечении трубопровода при значении угла α = 0 и давлении на свободной поверхности воды в резервуаре p1. Исходные данные приведены в таблице 3.88.
Задача 3-89
Из резервуара вытекает вода по трубопроводу переменного сечения с диаметрами d1, d2, d3 при напоре воды над осью входа в трубу H. Длины участков трубопровода соответственно l1, l2, l3. Построить пьезометрическую линию и определить давление p0 на свободной поверхности воды в резервуаре, необходимое для создания скорости в выходном сечении трубопровода υ3, если угол α ≠ 0. Исходные данные приведены в таблице.
Задача 3-90
Определить потери давления в стальном маслопроводе диаметром D и длиной при кинематической вязкости масла ν = 0,36 см2/с, плотности ρ = 900 кг/м3 и расходе Q. Исходные данные приведены в таблице 3.90.
Задача 3-91
Из бака при постоянном напоре H по прямому горизонтальному трубопроводу длиной и диаметром D вытекает вода в атмосферу (рис. 3.59), а на расстоянии 1 от начала трубопровода установлен вентиль. Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии, если λ = 0,03. Исходные данные приведены в таблице 3.91.
Задача 3-92
Определить расход в трубопроводе длиной = 120 м, построить пьезометрическую и напорную линии, если длина первого участка 1, его диаметр D1, диаметр второго участка D2, напор в баке H, отметка начала трубопровода Zн, отметка конца Zк, гидравлические коэффициенты трения λ1 и λ2 (рис. 3.60). Исходные данные приведены в таблице 3.92.
Задача 3-93
Из резервуара нефть протекает по стальному трубопроводу диаметром D = 250 мм и длиной l = 1 км. Плотность нефти ρ = 900 кг/м3, а кинематический коэффициент вязкости ν = 1 см2/с. Определить необходимый уровень нефти в резервуаре над входом в трубопровод, если уклон трубопровода i, а расход нефти Q.
Задача 3-94
Определить расход в стальном горизонтальном нефтепроводе диаметром D = 200 мм, при плотности нефти ρ = 880 кг/м3, кинематический коэффициент вязкости ν = 0,9 см2/с, если уровень нефти в резервуаре в начале нефтепровода Н, а длина его l.
Задача 3-95
При закрытом пробковом кране в трубе диаметром D избыточное давление составляет pизб/ρg. Определить на какой угол φ нужно повернуть пробковый кран, чтобы получить расход Q.
Задача 3-96
При закрытом пробковом кране в трубе диаметром D избыточное давление составляет pизб/(ρg) (рис. 3.61). Определить расход при повороте крана на угол φ. Исходные данные приведены в таблице 3.96а. Указание: коэффициенты потерь в кране в зависимости от угла поворота приведены в таблице 3.96б, а промежуточные значения следует определять линейной интерполяцией.
Задача 3-97
Из реки в колодец поступает вода с расходом Qпо трубе длиной l, имеющей сетку с обратным клапаном. Приняв коэффициент трения λ = 0,022, определить разность уровней Н в реке и в колодце при диаметре трубы d.
Задача 3-98
Из реки в колодец поступает вода с расходом Q по трубе длиной , имеющей сетку с обратным клапаном (рис. 3.62). Приняв коэффициент трения λ = 0,022, определить диаметр трубы при разности уровней в реке и в колодце H1. Исходные данные приведены в таблице 3.98. Указание: поскольку при неизвестном диаметре коэффициент трения по длине является неизвестным, задача решается методом последовательных приближений. Скоростями воды на свободной поверхности в реке и в колодце следует пренебречь.
Задача 3-99
Вода перетекает из одного бака в другой при постоянных уровнях по трубе переменного сечения, диаметры и длины соответственно равны 1, d1, 2 и d2, а коэффициенты трения λ1 = λ2 = 0,03 (рис. 3.63). Построить напорную и пьезометрическую линии и определить расход воды в трубе при H1 и H2. Исходные данные приведены в таблице 3.99.
Задача 3-100
Вода перетекает из одного бака в другой при постоянных уровнях по трубе переменного сечения, диаметры и длины соответственно равны 1, d1, 2 и d2, а коэффициенты трения λ1 = λ2 = 0,03 (рис. 3.63). Построить напорную и пьезометрическую линии и определить разность уровней воды в баках ΔH = H1 – H2 при расходе воды в трубе Q. Исходные данные приведены в таблице 3.100.
Задача 3-101
В двух закрытых резервуарах, соединенных трубой переменного сечения, при постоянной разнице уровней H = 1,5 м поддерживается постоянное манометрическое давление pм1 = 40 кПа и pм2 = 20 кПа (рис. 3.64). Участок трубы диаметром d2 имеет на боковой поверхности отверстие A, расположенное посередине участка, и проходит через резервуар B с водой, уровень которой совпадает с уровнем воды во втором резервуаре. Длины и диаметры участков 1 = 3; d1 = d3; 2; d2. Коэффициенты трения λ1 = λ2 = λ3 = 0,03. Определить, будет ли вода из отверстия A выходить в открытый резервуар или поступать в трубопровод, если h = 1,0 м и давление на свободной поверхности воды в резервуаре p0 = pат. Исходные данные приведены в таблице 3.101.
Задача 3-102
В двух резервуарах, соединенных трубой переменного сечения, при постоянной разнице уровней Н = 1,5 м поддерживается постоянное манометрическое давление pм1 = 40 кПа и pм1 = 20 кПа. Участок трубы диаметром d2 имеет на боковой поверхности отверстие А, расположенное посередине участка, и проходит через резервуар В с водой, уровень которой совпадает с уровнем воды во втором резервуаре. Длины и диаметры участков l1 = l3; d1 = d3; l2; d2. Коэффициенты трения λ1 = λ2 = λ3 = 0,03. Определить какое давление p0 должно быть на свободной поверхности в резервуаре В при h = 1,0 м, чтобы вода не выходила через отверстие А и не поступала в него.
Задача 3-103
В бак подается вода с постоянным расходом (рис. 3.65), а чтобы избежать переполнения бака, установлена сливная труба диаметром d и общей длиной l с коэффициентом трения λ = 0,025. Определить, при каком напоре H расходы притока и истечения воды из бака равны Q. Исходные данные приведены в таблице 3.103
Задача 3-104
В бак подается вода с постоянным расходом, а чтобы избежать переполнения бака, установлена сливная труба диаметром d и общей длиной с коэффициентом трения λ = 0,025 (рис. 3.65). Определить, какой расход Q должен поступать в бак, чтобы постоянный напор имел значение H1. Радиусы изгиба труб равны диаметру. Исходные данные приведены в таблице 3.104.
Задача 3-105
Из верхнего резервуара в нижний поступает вода при T °С по новому стальному сифонному трубопроводу диаметром D, длиной l и расходом (рис. 3.66). Расстояние от начала трубопровода до сечения 1–1 равно l1. Определить разность уровней H в резервуарах. Исходные данные приведены в таблице 3.105.
Задача 3-106
Из верхнего резервуара в нижний поступает вода при T°C по новому стальному сифонному трубопроводу диаметром D, длиной и расходом Q, а расстояние от начала трубопровода до сечения 1 – 1 равно 1 (рис. 3.66). Определить вакуум в наивысшей точке сифона при превышении ее отметки над уровнем воды в верхнем резервуаре h = 2,5 м. Исходные данные приведены в таблице 3.106. Указание: при решении задачи следует установить область гидравлических сопротивлений и в соответствии с ней принимать значение гидравлического коэффициента трения.
Задача 3-107
Определить скорость и расход жидкости Ж в вертикальной трубе, имеющей длину , диаметр d (рис. 3.67), если высота жидкости в баках H, диаметры обоих баков D, погружение нижнего конца трубы под уровень жидкости в нижнем баке a, показание жидкостного манометра, заполненного жидкостью М, равно h. Материал трубы Т. Исходные данные приведены в таблице 3.107.
Задача 3-108
Поршень диаметром D движется равномерно вверх в цилиндре, засасывая воду из открытого резервуара с постоянным уровнем. Когда поршень находится выше уровня воды в резервуаре на h, потребная для его перемещения сила равна F. Определить скорость подъема поршня, если длина и диаметр трубы l, d. Исходные данные приведены в таблице.
Задача 3-109
Определить напор H, который необходимо поддерживать в резервуаре (рис. 3.69), чтобы расход воды, пропускаемый по трубопроводу диаметром d, равнялся Q. Угол открытия крана α, длина трубы . Скоростным напором в резервуаре пренебречь. Построить линию удельной энергии и пьезометрическую линию (удельной потенциальной энергии). Исходные данные приведены в таблице 3.109.
Задача 3-110
Определить расход воды Q, пропускаемой по трубопроводу (рис. 3.69), при следующих данных: напор H, поддерживаемый в резервуаре, диаметр трубы d, угол открытия крана α, длина трубы . Исходные данные приведены в таблице 3.110.
Задача 3-111
Вода вытекает в атмосферу из резервуара по трубопроводу диаметром d (λ = 0,03; α = 30°). Каков должен быть коэффициент сопротивления ζз задвижки, чтобы вакуумметрическая высота в конце горизонтального участка не превосходила 7 м? Какой расход будет при этом в трубопроводе? Построить график полных напоров по длине трубопровода. Исходные данные приведены в таблице.
Задача 3-112
Найти, как распределяется расход воды Q между двумя параллельными трубами (рис. 3.71), одна из которых имеет задвижку (коэффициент сопротивления ее ζ3 = 4). Какова будет потеря напора в разветвленном участке? Исходные данные приведены в таблице 3.112.
Задача 3-113
Для подачи воды в количестве Q на расстояние под напором H (рис. 3.72) можно использовать чугунные трубы диаметрами d1 и d2. Определить необходимые длины участков трубопровода d1 и d2, принимая шероховатость труб Δ = 1,2 мм. Построить график напора. Исходные данные приведены в таблице 3.113.
Задача 3-114
Для подачи воды в количестве Q на расстояние l1 + l2 можно использовать чугунные трубы диаметрами d1 и d2 (рис. 3.72). Определить напор H воды в трубопроводе, принимая шероховатость труб Δ = 1,4 мм. Построить график напоров. Исходные данные приведены в таблице 3.114.
Задача 3-115
Определить расход жидкости Ж, перетекающей по вертикальной трубе, которая соединяет резервуары А и В (рис. 3.73), если диаметры труб d1 и d2, ее длины l1 и l2, разность уровней в резервуарах H. Показание жидкостного манометра h, жидкость в манометре Жм. Построить пьезометрическую линию. Исходные данные приведены в таблице 3.115.
Задача 3-116
Определить расход жидкости в горизонтальной трубе, соединяющей два резервуара, имеющей диаметры d1 и d2, длины 1 и 2 (рис. 3.74), если возвышение жидкости над осью трубы в левом сосуде равно hл, а в правом hп, показания манометров Mп и Mп соответственно pл и pп, превышение оси трубы над дном сосудов равно a.
Построить пьезометрическую линию. Исходные данные приведены в таблице 3.116.
Задача 3-117
Определить расход воды, протекающей из верхнего в нижний резервуар по системе труб, показанной на рисунке 3.75. Разность уровней воды в баках H. Диаметры труб (мм) указаны на схеме. Длина труб 1; 2; 3. Исходные данные приведены в таблице 3.117.
Задача 3-118
Зная расход воды Q, протекающей из верхнего в нижний резервуар по системе труб, показанной на рисунке 3.75, разность уровней воды в баках H, длины 1, 2, определить длину 3. Исходные данные приведены в таблице 3.118.
Задача 3-119
Зная расход воды Q, протекающей из верхнего в нижний резервуар по системе труб, показанной на рисунке 3.75, найти разность уровней воды в баках H, если диаметры труб (мм) указаны на схеме, длины труб 1, 2, 3. Исходные данные приведены в таблице 3.119.
Задача 3-120
Из нижнего бака с избыточным давлением pм по новой стальной трубе подается бензин в верхний бак, в котором поддерживается вакуум pвак (рис. 3.76). Разность уровней в баках h, длина трубы , диаметр d.
При каком значении коэффициента сопротивления вентиля ζвен будет подаваться расход Q? Коэффициент сопротивления трения определить по формуле П. Н. Конакова для гидравлически гладких труб. Исходные данные приведены в таблице 3.120.
Задача 3-121
Определить расход воды Q, протекающей по трубопроводу, если известны pм, pвак, h, , d, ζвен (рис. 3.76). Исходные данные приведены в таблице 3.121.
Задача 3-122
Вода подается из нижнего закрытого бака в верхний открытый бак по вертикальной трубе за счет избыточного давления в нижнем баке pм (рис. 3.77). Определить расход воды Q при h1 = h2 = 1,2 м. Коэффициент сопротивления трения определить по эквивалентной шероховатости Δ = 0,2 мм, предполагая наличие квадратичной зоны сопротивления, ζвен = 4,0. Исходные данные приведены в таблице 3.122.
Задача 3-123
Вода подается из нижнего закрытого бака в верхний открытый бак по вертикальной трубе за счет избыточного давления pизб (см. рис. 3.77), которое нужно определить, если расход воды Q, диаметр трубы d, длина ее ; h1 = h2 = 1,2 м. Коэффициент сопротивления трения определить по эквивалентной шероховатости Δ = 0,2 мм, предполагая наличие квадратичной зоны сопротивления, коэффициент местного сопротивления вентиля ζв = 4,5. Исходные данные приведены в таблице 3.123.
Задача 3-124
Вода подается из нижнего закрытого бака в верхний открытый бак по вертикальной трубе за счет избыточного давления в нижнем баке pизб (см. рис. 3.77). Определить длину трубы при h1 = h2 = 1,2 м, ζвен = 4,2, при известных d и Q. Коэффициент сопротивления трения определить по эквивалентной шероховатости Δ = 0,2 мм, предполагая наличие квадратичной зоны сопротивления. Исходные данные приведены в таблице 3.124.
Задача 3-125
Определить максимально допустимую высоту установки насоса h над уровнем воды в бассейне (рис. 3.78) при следующих данных: производительность насоса Q, допустимый вакуум во всасывающем патрубке pвак, длина всасывающей трубы , диаметр d. Всасывающая труба снабжена приемным клапаном с сеткой (ζкл = 6) и имеет одно сварное колено (ζкол = 1,2). Коэффициент сопротивления трения определить по эквивалентной шероховатости Δ = 0,2 мм, предполагая наличие квадратичной зоны сопротивления. Исходные данные приведены в таблице 3.125.
Задача 3-126
Определить длину всасывающей трубы (рис. 3.78), если труба снабжена приемным клапаном с сеткой (ζкл = 6) и имеет одно сварное колено (ζкол = 1,2).
Коэффициент сопротивления трения определить по эквивалентной шероховатости Δ = 0,2 мм, предполагая наличие квадратичной зоны сопротивления. Известны расход Q, вакуум pвак, диаметр d и h. Исходные данные приведены в таблице 3.126.
Задача 3-127
Определить давление pвак во всасывающем патрубке, если всасывающая труба (см. рис. 3.78) снабжена приемным клапаном с сеткой (ζкл = 6) и имеет одно сварное колено (ζкол = 1,2). Коэффициент сопротивления трения определить по эквивалентной шероховатости Δ = 0,2 мм, предполагая наличие квадратичной зоны сопротивления. Известны Q, h, , d. Исходные данные приведены в таблице 3.127.
Задача 3-128
Определить расход воды при Δ = 0,2 мм, если известны h, pвак, l, d, ζкл, ζкол (см. рис. 3.78). Исходные данные приведены в таблице 3.128.
Задача 3-129
Из резервуара вытекает вода по трубопроводу переменного сечения с диаметрами d1, d2, d3 при уровне воды над осью трубы H (рис. 3.79). Длины участков 1, 2, 3. Определить давление на свободной поверхности воды в резервуаре p0, необходимое для создания скорости движения v3 воды в выходном сечении трубопровода. Исходные данные приведены в таблице 3.129.
Задача 3-130
Из резервуара вытекает вода по новому чугунному трубопроводу переменного сечения с диаметрами d1, d2, d3 при уровне воды над осью трубы H. Длины участков l1, l2, l3. Построить пьезометрическую линию, определить расход и скорость движения воды в выходном сечении трубопровода, если давление на свободной поверхности резервуара.
Задача 3-131
По самотечному сифонному трубопроводу (Δ = 0,2 мм) длиной необходимо обеспечить расход нефти Q при напоре H (рис. 3.80). Найти требуемый диаметр трубопровода, учитывая только потери на трение.
Определить допустимое превышение h сечения C, если оно находится на середине длины трубопровода, а вакуум не должен превышать pвак. Исходные данные приведены в таблице 3.131.
Задача 3-132
По самотечному трубопроводу (Δ = 0,35 мм) длиной (рис. 3.80) необходимо обеспечить расход Q бензина при напоре H, учитывая только потери на трение. Определить давление в точке C, если длина восходящей линии до точки С 1 = и известно h. Исходные данные приведены в таблице 3.132.
Задача 3-133
По сифонному трубопроводу с напором необходимо подавать воду расходом Q при условии, чтобы вакуумметрическая высота в сечении трубопровода C не превышала 7 м (рис. 3.81); длина восходящей линии до этого сечения 1 = 100 м, а нисходящей 2 = 60 м. Трубопровод снабжен приемным клапаном с сеткой (ζкл = 5) и задвижкой. Определить диаметр трубопровода d и коэффициент сопротивления задвижки ζ3. Построить график напоров по длине трубопровода. Коэффициент сопротивления трения λ = 0,025, известно h. Исходные данные приведены в таблице 3.133.
Задача 3-134
Из одного резервуара в другой вода поступает по сифонному трубопроводу длиной и диаметром d (рис. 3.81). Определить расход воды Q при разности уровней в резервуарах H. Трубопровод снабжен приемным клапаном с сеткой (ζкл = 5) и задвижкой (ζ3 = 4). Потерями напора в коленах и на выходе из трубы пренебречь. Коэффициент сопротивления трения λ = 0,03. Найти вакуум в опасной точке сифона, если длина участка трубопровода до этой точки 1 и ее возвышение над уровнем воды в верхнем резервуаре h. Исходные данные приведены в таблице 3.134.
Задача 3-135
Наполнение бассейна из магистрали с заданным избыточным давлением pм (рис. 3.82) производится по горизонтальной чугунной трубе (Δ = 1 мм) общей длиной , снабженной вентилем (ζв = 2). Определить диаметр трубы, который обеспечит наполнение бассейна количеством воды V за время t = 30 мин. Построить график напора. Исходные данные приведены в таблице 3.135.
Задача 3-136
Определить расход воды Q, подаваемой насосом в водонапорный бак (рис. 3.83), при следующих данных: высота расположения центробежного насоса над уровнем воды в водоеме — hн, вакуум во всасывающей трубе насоса равен pвак, длина всасывающей трубы и диаметр d. Для определения потерь напора принять сопротивление на входе (сетки) ζс = 6,0; сопротивление в колене ζк = 0,6; коэффициент гидравлического трения λ = 0,03. Исходные данные приведены в таблице 3.136.
Задача 3-137
Для подачи воды из канала в отводной лоток с расходом Q установлен металлический сифон длиной и диаметром d (рис. 3.84). Коэффициент гидравлического трения λ = 0,02. На сифоне имеются два поворота (ζпов = 0,15) и сетка на входе ζ = 5). Разность уровней воды H. Определить высоту установки горизонтального участка сифона над уровнем воды в канале (Z), при которой вакуум в точке C, отстоящей от входа в сифон на расстояние 1, не будет превышать pвак = 30 кПа. Исходные данные приведены в таблице 3.137.
Задача 3-138
Определить, при какой разности уровней воды в баках по системе труб будет протекать вода с расходом Q, если известны диаметры труб и длины труб.
Задача 3-139
Вода вытекает в атмосферу из закрытого резервуара, имеющего ртутный манометр, по новой чугунной трубе переменного сечения с диаметрами d1, d2 и длинами 1, 2 при напоре H (рис. 3.86). Построить пьезометрическую линию и определить показания ртутного манометра h, если расход воды Q. Исходные данные приведены в таблице 3.139.
Задача 3-140
Какой расход воды Q нужно пропустить по новому чугунному трубопроводу (рис. 3.87), если напор H = 3 м, кран открыт на угол β. Построить пьезометрическую и напорную линии, если α = 30°, известны d, , z. Исходные данные приведены в таблице 3.140.
Задача 3-141
Определить напор H1, который нужно создать в резервуаре, чтобы расход воды в трубопроводе был Q. Угол открытия крана β. Скоростным напором в резервуаре пренебречь. Известны d, l, z.
Задача 3-142
Определить скорость воды в трубопроводе длиной , диаметром d при открытии крана на угол β (рис. 3.87), если выходное отверстие расположено на Z ниже входного. Значение напора H = 5,6 м. Построить пьезометрическую и напорную линии. Исходные данные приведены в таблице 3.142.
Задача 3-143
Определить расход и скорость истечения воды на выходе из трубопровода в атмосферу (рис. 3.88) для двух случаев: с учетом потерь напора и без учета потерь. Построить пьезометрическую и напорную линии для вязкой жидкости. Известны длины и диаметры труб и напор H. Исходные данные приведены в таблице 3.143.
Задача 3-144
Вода расходом Q поступает из напорного бака A в бак B по двум параллельно соединенным трубопроводам (рис. 3.89). Определить отметку HA горизонта воды в напорном баке и расходы Q1 и Q2 по параллельным ветвям 1 и 2, если известны 1, 2, d1 и d2. Исходные данные приведены в таблице 3.144.
Задача 3-145
В системе трубопроводов определить скорость истечения и расход воды при угле α = 45°, λзад = 2,5 и заданных величинах: H, 1, 2, , d1, d2, d3 (рис. 3.90).
Исходные данные приведены в таблице 3.145.
Задача 3-146
Определить расход воды Q, протекающей из бака A в бак B по системе труб, и расходы Q1, Q2, Q3, если известны длины и диаметры труб (рис. 3.91). Исходные данные приведены в таблице 3.146.
Задача 3-147
В трубопроводе с параллельными линиями заданы длины 1, 2, 3, BC, диаметры d1, d2, d3, dBC и пьезометрический напор в точке C — HC. Определить необходимый напор в точке A трубопровода и расходы в параллельных ветвях 1, 2, 3, если общая подача воды из точки A в точку C должна быть Q (рис. 3.92). Исходные данные приведены в таблице 3.147.
Задача 3-148
Определить расходы воды в трубопроводе Q1, Q2, Q3, если известны напор H, ζ3 = 30, длины и диаметры труб (рис. 3.93). Исходные данные приведены в таблице 3.148.
Задача 3-149
Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте H и постоянное давление p2 (рис. 3.94). Манометр, установленный на выходе из насоса на трубе диаметром d1, показывает давление p1. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, равен d2; коэффициент сопротивления этой трубы принят ζ = 0,5. Плотность жидкости ρ = 800 кг/м3. Исходные данные приведены в таблице 3.149.
Задача 3-150
Вода перетекает из напорного бака, где избыточное давление воздуха p, в открытый резервуар по короткой трубе диаметром d, на которой установлен кран (рис. 3.95). Чему должен быть равен коэффициент сопротивления крана для того, чтобы расход воды составлял Q? Высоты уровней имеют значения H1 и H2. Учесть потерю напора на входе в трубу (ζвх = 0,5) и на выходе из трубы (внезапное расширение). Исходные данные приведены в таблице 3.150.
Задача 3-151
Для измерения расхода воды, которая подается по трубе А в бак Б, установлен расходомер Вентури В (рис. 3.96). Определить максимальный расход, который можно пропускать через данный расходомер при условии отсутствия в нем кавитации, если температура воды T (давление насыщенных паров соответствует hн.п = 2,0 мм вод. ст.). Уровень воды в баке поддерживается постоянным, равным H и h. Размеры расходомера приняты d1 и d2. Атмосферное давление принять равным 760 мм рт. ст. Коэффициент сопротивления диффузора ζдиф = 0,2. Исходные данные приведены в таблице 3.151.
Задача 3-152
Вода плотностью ρ = 1000 кг/м3 перетекает из верхнего резервуара в нижний по расширяющейся трубе диффузору, имеющей малый угол конусности и плавно закругленный вход (рис. 3.97). Пренебрегая потерей напора на входе в диффузор, определить, при каком уровне воды H1 в верхнем резервуаре абсолютное давление в узком сечении 1 – 1 диффузора сделается равным нулю. Коэффициент сопротивления диффузора ζдиф = 0,2.
Размеры диффузора: d1 и d2. Известно значение H2. Учесть потерю на внезапное расширение при выходе из диффузора. Атмосферное давление 750 мм рт. ст. Указание: учесть потерю кинетической энергии на выходе из диффузора по формуле Борда–Карно. Исходные данные приведены в таблице 3.152.
Задача 3-153
Бензин сливается из цистерны по трубе диаметром d, на которой установлен кран с коэффициентом сопротивления ζкр = 3,0. Определить расход бензина при H1 и H2, если в верхней части цистерны имеет место вакуум hвак. Потерями на трение в трубе пренебречь. Плотность бензина ρб = 750 кг/м3.
Задача 3-154
Определить расход воды, вытекающей из бака через короткую трубку (насадок) диаметром d и коэффициентом сопротивления ζ = 0,5, если показание ртутного манометра hрт (рис. 3.99).Также известны значения H1, H0, . Исходные данные приведены в таблице 3.154.
Задача 3-155
При внезапном расширении трубы от d до D получается увеличение давления, которому соответствует разность показаний пьезометров Δh (рис. 3.100). Определить, при каком соотношении площадей широкого и узкого сечений трубы (n = D2/d2) увеличение давления будет наибольшим. Выразить величину Δhmax через скорость в узком сечении. Исходные данные приведены в таблице 3.155.
Задача 3-156
Сравнить коэффициенты сопротивления мерного сопла d, установленного в трубе D, и расходомера Вентури, состоящего из такого же сопла диаметром d и диффузора (рис. 3.101). Коэффициенты сопротивления определить как отношение суммарной потери напора к скоростному напору в трубопроводе. Дано отношение диаметров D/d. Принять коэффициенты сопротивлений: сопла ζс = 0,05; диффузора ζдиф = 0,15 (оба коэффициента относятся к скорости в узком сечении). Определить потери напора, вызываемые мерным соплом hс и расходомером hр при одинаковой скорости потока в трубе υ. Указание: на выходе из сопла учесть потери напора на внезапное расширение. Исходные данные приведены в таблице 3.156.
Задача 3-157
Определить расход жидкости, вытекающей из трубы диаметром d через плавное расширение (диффузор) и далее по трубе диаметром D в бак (рис. 3.102). Коэффициент сопротивления диффузора ζ = 0,2 (отнесен к скорости в трубе), показание манометра pн = 20,0 кПа; высоты h и H; плотность жидкости ρ = 1000 кг/м3. Учесть потери на внезапное расширение; потерями на трение пренебречь; режим течения считать турбулентным. Исходные данные приведены в таблице 3.157.
Задача 3-158
Вода перетекает из бака А в резервуар Б по трубе длиной и диаметром d, на которой установлены вентиль ζ = 3,5 и диффузор с углом α = 8° и диаметром выходного отверстия D (рис. 3.103). Показание мановакуумметра pвак, высоты H и h. Определить расход Q с учетом всех местных сопротивлений и трения по длине (λ = 0,03). Вход в трубу без закруглений, радиус кривизны колен R = 25 мм. Взаимным влиянием сопротивлений пренебречь. Исходные данные приведены в таблице 3.158.
Задача 3-159
Вода перетекает из напорного бака А в резервуар Б через вентиль с коэффициентом сопротивления ζв = 3,0 по трубе. Даны диаметры d1 и d2. Считая режим течения турбулентным и пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Известны высоты H1 и H2; избыточное давление в напорном баке p0. Исходные данные приведены в таблице 3.159.
Задача 3-160
Определить минимальное давление pм, измеряемое манометром при сужении трубы, при котором будет происходить подсасывание воды из резервуара A в узком сечении трубы (рис. 3.105). Известны размеры: d1, d2, H1 и H2. Принять коэффициенты сопротивления: сопла ζс = 0,08 и диффузора ζдиф = 0,30. Исходные данные приведены в таблице 3.160.
Задача 3-161
Определить потерю давления в диффузоре с начальным d и конечным D диаметрами, если вязкость жидкости ν – 1 Ст; плотность ρ = 900 кг/м3; расход Q; угол диффузора α = 9º. При решении задачи считать, что в любом сечении диффузора существует стабилизированное ламинарное течение и справедлив закон Пуазейля.
Задача 3-162
В водоструйном насосе-эжекторе вода под давлением p0 подводится по трубе диаметром d в количестве Q (рис. 3.107). Сопло сужает поток до величины dс и тем самым увеличивает скорость, понижая давление. Затем в диффузоре происходит расширение потока до величины d и повышение давления. Вода выходит в атмосферу на высоте H2. Таким образом, в камере К создается вакуум, который заставляет воду подниматься из нижнего резервуара на высоту H1. Определить минимальное давление p0 перед эжектором, при котором возможен подъем воды на высоту H1. Учесть потери напора в сопле ζ = 0,06), в диффузоре (ζдиф = 0,25) и в коленах (ζк = 0,25) для каждого. Коэффициенты отнесены к скорости в трубе с диаметром d. Исходные данные приведены в таблице 3.162.
Часть задач есть решенные, контакты
4. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДОК ПРИ ПОСТОЯННОМ И ПЕРЕМЕННОМ НАПОРЕ
Задача 4—1
Определить суммарный расход воды Q1 из резервуара через два отверстия в его стенке: круглое диаметром d, расположенное на расстоянии e от дна, и квадратное со стороной a, примыкающее одной стороной к дну (рис. 4.7). Глубина воды в резервуаре h. Каков будет суммарный расход Q2, если к верхнему отверстию присоединить цилиндрический насадок? Исходные данные представлены в таблице 4.1.
Задача 4-2
В теле железобетонной плотины имеется водоспуск в виде трубы длиной (рис. 4.8). Напор над водоспуском при свободном истечении H1. Разность отметок ВБ и НБ составляет H2. Скорость подхода воды к плотине υ. Определить диаметр водоспуска, если расход Q = 12 м3/с. Установить, какой расход будет через водоспуск, если уровень нижнего бьефа поднимется на h = 10м. Исходные данные представлены в таблице 4.2.
Задача 4-3
Вода вытекает из открытого бака через цилиндрический насадок диаметром d при постоянном напоре H в атмосферу. Сосуд емкостью V, подставленный под струю, наполнился за t секунд. Определить коэффициент потерь насадка и потери напора в насадке. Исходные данные представлены в таблице 4.3.
Задача 4-4
Отверстие в виде равностороннего треугольника со стороной a перекрыто щитом (рис. 4.9). Щит поднимается равномерно со скоростью v. Определить объем воды, вытекающей за время t полного открытия отверстия. Напор перед щитом отверстия H1 = const. Истечение свободное. Коэффициент расхода отверстия μ = 0,58 = const. Исходные данные представлены в таблице 4.4.
Задача 4-5
Насос подает воду в резервуар в количестве Q0 (рис. 4.10). Высота резервуара h, диаметр – D. В дне имеется круглое отверстии диаметром d, через которое вода вытекает в атмосферу. Определить, в течение какого времени насос должен подавать воду в резервуар, чтобы наполнить его до краев, если в начальный момент времени глубина воды в резервуаре равна Н1. Исходные данные представлены в таблице 4.5.
Задача 4-6
На поршень диаметром D действует сила F (рис. 4.11). Определить скорость движения поршня при диаметре отверстия в поршне d и толщине поршня a. Исходные данные представлены в таблице 4.6.
Задача 4-7
Вертикальный цилиндрический бак имеет размеры: высоту h и радиус поперечного сечения r. В дне бака сделано отверстие диаметром d. Глубина воды в баке H. Определить объем воды в баке через t минут после открытия отверстия, если постоянный приток воды в бак Q0. Исходные данные представлены в таблице 4.7.
Задача 4-8
Постоянный приток воды в резервуар составляет Q0 (рис. 4.12). В дне резервуара сделано отверстие ω Площадь нижней части резервуара Ω1, верхней — Ω2. К моменту открытия отверстия глубина воды над отверстием равнялась 2a. Через какое время после открытия отверстия глубина воды над ним будет равна a/2? Исходные данные представлены в таблице 4.8.
Задача 4-9
Из цилиндрического бака с площадью поперечного сечения Ω вытекает вода через отверстие диаметром d в дне. Через 30 мин после открытия отверстия глубина в баке оказалась равной h. Сколько литров воды вытекло за первые t минут? Исходные данные представлены в таблице 4.9.
Задача 4-10
Определить время опорожнения цилиндрического сосуда, имеющего площадь поперечного сечения Ω, глубину воды h (рис. 4.13) в трех случаях истечения:
1) через круглое отверстие диаметром d в дне сосуда;
2) через вертикальный цилиндрический насадок диаметром d и длиной н, присоединенный к отверстию в дне;
3) через вертикальную трубу диаметром d, длиной , присоединенную так же, как и насадок. Коэффициент расхода системы в этом случае принять μ = 0,7. Исходные данные представлены в таблице 4.10.
Задача 4-11
Из закрытого резервуара в атмосферу вытекает вода через отверстие диаметром d в тонкой стенке и внешний цилиндрический насадок диаметром d (рис. 4.14). Определить манометрическое давление pм на свободной поверхности воды в резервуаре, если разность расходов отверстия и насадка ΔQ, а напор над центром отверстия и насадка – H. Исходные данные представлены в таблице 4.11.
Задача 4-12
Определить расход и давление в отверстии плотины при заданных d, l = 4d и H (рис. 4.15). Исходные данные представлены в таблице 4.12.
Задача 4-13
Из водохранилища вода вытекает через отверстие в плотине диаметром d (рис. 4.15). Определить время, за которое уровень воды в водохранилище опустится на h, если начальный напор H, а толщина плотины , при условии, что площадь зеркала воды в водохранилище Ω не изменяется с изменением уровня. Исходные данные представлены в таблице 4.13.
Задача 4-14
Бак с квадратным основанием a х a и высотой H заполнен доверху водой. Найти время, за которое из бака вытечет половина воды через внешний цилиндрический насадок диаметром d в дне бака. Исходные данные представлены в таблице 4.14.
Задача 4-15
Призматический бак с прямоугольным основанием a×b разделен пополам перегородкой на два отсека, в которой имеется отверстие с цилиндрическим насадком диаметром d (рис. 4.16). Высота бака H, глубина воды в левом отсеке H1 поддерживается постоянной; насадок расположен на высоте l1 от дна. Принимая, что в начальный момент правый отсек пуст, определить время его наполнения. Исходные данные представлены в таблице 4.15.
Задача 4-16
В баке, имеющем в дне отверстие диаметром d1, а в стенке — отверстие, снабженное цилиндрическим насадком диаметром d2, установился уровень воды на высоте H (рис. 4.17). Определить, каков расход воды Q, поступающей в бак, если центр бокового отверстия возвышается над дном бака на высоту h. Определить скорости истечения из отверстия υ и насадка v2. Исходные данные представлены в таблице 4.16.
Задача 4-17
В бак, имеющий в дне отверстие диаметром d1, а в стенке отверстие, снабженное цилиндрическим насадком диаметром d2, поступает вода расходом Q (рис. 4.17). Определить уровень воды Н, если центр бокового отверстия возвышается над дном бака на высоте h.
Исходные данные представлены в таблице 4.17.
Задача 4-18
В бак, разделенный тонкой перегородкой на два отсека (рис. 4.18), поступает вода. В перегородке имеется отверстие диаметром d1. Из второго отсека вода сливается наружу через конический насадок диаметром d2. При напоре H1 определить расход Q. Исходные данные представлены в таблице 4.18.
Задача 4-19
В бак, разделенный тонкой перегородкой на два отсека, поступает вода расходом Q (рис. 4.18). В перегородке имеется отверстие диаметром d1. Из второго отсека вода сливается наружу через конический насадок диаметром d2. Зная напор H1, определить диаметр d2. Исходные данные представлены в таблице 4.19.
Задача 4-20
В бак, разделенный тонкой перегородкой на два отсека, поступает вода расходом Q (рис. 4.19). В дне каждого отсека имеются одинаковые отверстия диаметром d1 = d2, а в перегородке — отверстие диаметром d3. Определить напоры H1 и H2. Исходные данные представлены в таблице 4.20.
Задача 4-21
В бак, разделенный тонкой перегородкой на два отсека, поступает вода расходом Q (рис. 4.19). В дне каждого отсека имеются одинаковые отверстия диаметром d1 = d2, а в перегородке — отверстие диаметром d3. Определить расходы воды Q1 и Q2, проходящие через донные отверстия. Исходные данные представлены в таблице 4.21.
Задача 4-22
Через круглое отверстие диаметром d, расположенное на глубине H от поверхности, из резервуара, находящегося под избыточным давлением p0, в атмосферу вытекает вода (рис. 4.20). Определить, насколько увеличится расход воды после присоединения к отверстию цилиндрического насадка. Исходные данные представлены в таблице 4.22.
Задача 4-23
Определить время t опорожнения цилиндрического резервуара, заполненного водой и имеющего диаметр D и высоту H (рис. 4.21), если отверстие в дне имеет площадь S = 0,0176 м2. Исходные данные представлены в таблице 4.23.
Задача 4-24
Цилиндрический бак имеет в дне два отверстия равного диаметра (рис. 4.22). Одно из отверстий снабжено внешним насадком. Какой диаметр должны иметь отверстия, чтобы при поступлении в бак воды расходом Q уровень в нем поддерживался на высоте Н? Определить скорости истечения воды. Исходные данные представлены в таблице 4.24.
Задача 4-25
В стенке, разделяющей резервуар на две части, у дна расположено квадратное отверстие со стороной а, через которое проходит вода в количестве Q1 (рис. 4.23). Глубина воды в левой части резервуара постоянная и равна Н1. Определить диаметр d круглого отверстия в наружной стенке правой части, а если центр отверстия расположен на расстоянии от дна, и расход Q2 в случае, если к наружному отверстию присоединить цилиндрический насадок. Исходные данных представлены в таблице 4.25.
Задача 4-26
В бак, разделенный тонкой перегородкой на два отсека, поступает расход воды Q (рис. 4.24). В перегородке имеется отверстие диаметром d1. Из второго отсека вода сливается наружу через цилиндрический насадок диаметром d2. Определить глубину воды в отсеках над центром отверстий. Исходные данные представлены в таблице 4.26.
Задача 4-27
Два круглых отверстия с острой кромкой диаметрами d1 = d2 расположены одно под другим в вертикальной стенке резервуара (рис. 4.25). Определить суммарный расход из обоих отверстий Q, если известен напор H, расстояния a1, a2. Исходные данные представлены в таблице 4.27.
Задача 4-28
Определить расход Q при истечении через отверстие с острой кромкой диаметром d под напором H (рис. 4.26) следующих жидкостей: а) морской воды; б) нефти. Исходные данные представлены в таблице 4.28.
Задача 4-29
Определить напор H в резервуаре, который обеспечил бы расход воды Q через малое отверстие с острой кромкой диаметром d. Исходные данные представлены в таблице 4.29.
Задача 4-30
Определить, какого диаметра d должно быть малое отверстие с острой кромкой в боковой стенке резервуара, чтобы при напоре H через него проходил расход воды Q. Исходные данные представлены в таблице 4.30.
Задача 4-31
Жидкость перетекает из открытого левого бака в закрытый правый бак (рис. 4.27). Определить расход жидкости, протекающей через цилиндрический насадок диаметром d = 60 мм, если известны глубины H1, H2 и показание вакуумметра pвак. Исходные данные представлены в таблице 4.31.
Задача 4-32
Бензин перетекает из открытой левой секции бака в закрытую правую через цилиндрический насадок (рис. 4.27). Определить, какое давление должно быть над поверхностью бензина в правой секции, чтобы при заданных уровнях H1 и H2 через насадок диаметром d протекало количество жидкости Q. Исходные данные представлены в таблице 4.32.
Задача 4-33
Определить расход воды, вытекающей из большого бака через внутренний цилиндрический насадок, диаметр которого d, напор истечения H (рис. 4.28). Как изменится расход, если насадок убрать, оставив только отверстие в тонкой стенке? Исходные данные представлены в таблице 4.33.
Задача 4-34
Определить, при каком напоре H из бака через внутренний цилиндрический насадок диаметром d будет вытекать количество воды Q (см. рис. 4.28). Как изменится напор, если насадок убрать, оставив только отверстие в тонкой стенке? Исходные данные представлены в таблице 4.34.
Задача 4-35
Квадратное отверстие в стенке резервуара примыкает одной стороной размером a ко дну (рис. 4.29). Определить, при какой глубине воды в резервуаре расход через отверстие будет Q. Исходные данные представлены в таблице 4.35.
Задача 4-36
Квадратное отверстие в стенке резервуара примыкает одной стороной a ко дну (рис. 4.30). Определить расход бензина Q1, вытекающего из бака через цилиндрический насадок, и Q2 — через отверстие, если напор H, диаметр dн = a, = 2a. Исходные данные представлены в таблице 4.36.
Задача 4-37
В верхний сосуд поступает расходом Q вода, которая затем перетекает через цилиндрический насадок в дне диаметром d1 в нижний сосуд, имеющий отверстие в дне диаметром d2 (рис. 4.31). Определить напоры H1 и H2. Исходные данные представлены в таблице 4.37.
Задача 4-38
В верхний сосуд поступает вода расходом Q, которая затем перетекает через цилиндрический насадок в дне диаметром d1 в нижний сосуд, имеющий отверстие в дне диаметром d2, снабженное коническим насадком (рис. 4.32). Зная напоры H1 и H2, определить расход Q и диаметр насадка d2. Исходные данные представлены в таблице 4.38.
Задача 4-39
Цилиндрический бак имеет в дне два отверстия разного диаметра (рис. 4.33). Одно из отверстий снабжено коническим сходящимся насадком. Какой диаметр должны иметь отверстия, чтобы при поступлении в бак расхода Q уровень в нем поддерживался на высоте H? Определить скорости истечения. Исходные данные представлены в таблице 4.39.
Задача 4-40
Определить время t опорожнения резервуара с водой через цилиндрический насадок диаметром d, если известны Ω1, Ω2, H1, H2 (рис. 4.34). Исходные данные представлены в таблице 4.40.
Задача 4-41
Определить избыточное давление pизб сжатого воздуха над поверхностью жидкости в баке при начальном расходе жидкости Q через цилиндрический насадок диаметром d (рис. 4.35). Уровень жидкости в баке. Исходные данные представлены в таблице 4.41.
Задача 4-42
Определить расход бензина Q, проходящего через внешний цилиндрический насадок диаметром d, если напор в баке H, давление сжатого воздуха над поверхностью жидкости pизб (рис. 4.35). Исходные данные представлены в таблице 4.42.
Задача 4-43
Определить время t опорожнения резервуара с водой, в дне которого имеется отверстие площадью S (рис. 4.36). Исходные данные представлены в таблице 4.43.
Задача 4-44
В дорожной насыпи устраивается труба — выпуск по типу конического расходящегося насадка (рис. 4.37). Определить диаметры входной и выходной частей трубы — насадка при условии, что насадок будет затопленным. Даны: расход Q, разность горизонтов Z, длина трубы, угол конусности θ = 6°. Исходные данные представлены в таблице 4.44.
Задача 4-45
В бак, разделенный перегородкой на два отсека, подается вода в количестве Q (рис. 4.38). Температура жидкости 20°C. В перегородке имеется цилиндрический насадок, диаметр которого d1, а длина = 3d1. Жидкость из второго отсека через отверстие диаметром d2 поступает наружу, в атмосферу. Определить напоры H1 и H2 уровней жидкости. Исходные данные представлены в таблице 4.45.
Задача 4-46
Через водоспуск плотины, имеющей форму цилиндрического насадка, необходимо пропускать расход Q при глубинах подтопления насадка H1 и H2. Определить диаметр водоспуска d (рис. 4.39). Исходные данные представлены в таблице 4.46.
Задача 4-47
В бак, разделенный на две секции перегородкой, имеющей отверстие диаметром d, поступает вода в количестве Q (рис. 4.40). Из каждой секции вода вытекает через цилиндрический насадок, диаметр которого равен d. Определить расход через левый Qл и правый Qп насадки при установившемся режиме, предполагая, что отверстие в перегородке является затопленным, если Z = 0,5 м. Исходные данные представлены в таблице 4.47.
Задача 4-48
В теле железобетонной плотины проектируется водоспуск в виде трубы длиной = 5 м (рис. 4.41). Напор над водоспуском при свободном истечении равен H1, разность отметок уровней воды в верхнем и нижнем бьефах плотины H2 = 15 м. Скорость подхода воды к плотине υ = 0,4 м/с. Определить диаметр d водоспуска, если расход воды Q. Исходные данные представлены в таблице 4.48.
Задача 4-49
В плотине скорость подхода воды к водоспуску υ0 = 0,6 м/с, длина трубы (рис. 4.41). Напор над водоспуском H1, а в нижнем бьефе плотины H2, диаметр трубы d. Определить расход воды Q, пропускаемой через плотину. Исходные данные представлены в таблице 4.49.
Задача 4-50
Определить время t опорожнения цилиндрического резервуара, заполненного водой и имеющего диаметр d и высоту H, если к отверстию в дне площадью S = 0,0176 м2 присоединить внешний цилиндрический насадок (рис. 4.42). Исходные данные представлены в таблице 4.50.
Задача 4-51
Пренебрегая потерями, определить расход Q и начальную скорость истечения v через конический насадок диаметром d из сосуда, заполненного слоями воды и масла (объемный вес γм = 7848 Н/м3) одинаковой высоты H (рис. 4.43). Сравнить полученный результат с начальной скоростью при заполнении сосуда только водой до уровня 2H. Исходные данные представлены в таблице 4.51.
Задача 4-52
Жидкость в баке находится под давлением pизб = 0,13 МПа (рис. 4.44). Определить расход Q и скорость истечения жидкости из сосуда v, заполненного слоями воды и масла одинаковой высоты H. Определить начальную скорость истечения и расход при заполнении сосуда только водой до уровня 2H и диаметре отверстия d. Исходные данные представлены в таблице 4.52.
Задача 4-53
Цилиндрический бак диаметром D имеет в дне два одинаковых отверстия, одно из которых снабжено внешним цилиндрическим насадком (рис. 4.45). Какой диаметр должны иметь отверстия, чтобы при поступлении в бак количества воды Q уровень поддерживался на высоте H? Определить, за какое время t произойдет опорожнение сосуда только через цилиндрический насадок после прекращения притока воды в бак, используя найденный диаметр насадка. Исходные данные представлены в таблице 4.53.
Задача 4-54
Призматический бак высотой H с дном площадью S соединен с резервуаром цилиндрическим насадком диаметром d (рис. 4.46). Расстояние от дна бака до центра отверстия h. Определить, за какое время t наполнится бак, если уровень воды в резервуаре не меняется. Исходные данные представлены в таблице 4.54.
Задача 4-55
Определить, какой объем воды V был налит в цилиндрический бак диаметром D, если вся вода вытекает из него через отверстие в дне диаметром d за время t (рис. 4.47). Какое время t1 потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза? Исходные данные представлены в таблице 4.55.
Задача 4-56
Определить расход воды через отверстие с острой кромкой диаметром d, выполненное в торце трубы диаметром D (рис. 4.48), если показание манометра перед отверстием pм и высота расположения манометра над осью трубы h. Как изменится расход, если к отверстию присоединить цилиндрический насадок (штриховая линия)? Исходные данные представлены в таблице 4.56.
Задача 4-57
Через отверстие с острой кромкой диаметром d, выполненное в торце трубы диаметром D = 250 мм, вытекает вода в атмосферу в количестве Q (рис. 4.48). Определить показание манометра, если высота расположения его над осью трубы h. Как изменится показание манометра, если к отверстию присоединить цилиндрический насадок (штриховая линия)? Исходные данные представлены в таблице 4.57.
Задача 17
По нефтепроводу диаметром d = 200 мм и длиной l = 4 км перекачивается нефть с расходом 108 м3/ч, удельным весом γн = 900 кгс/м3 и кинетическим коэффициентом вязкости ν = 1 см2/сек. Определить необходимое давление в начале трубопровода, если он проложен по горизонтальной местности. Трубопровод стальной, нефть вытекает в подземный резервуар, сообщаемый с атмосферой.
Задача 13
Определить разность давления в резервуарах А и В, заполненных бензином, если показание дифференциального манометра hр задано.
|
№ вар |
hр, мм |
|
1 |
70 |
Часть задач есть решенные, контакты


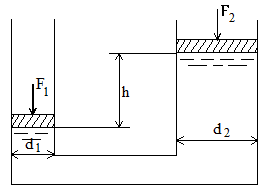


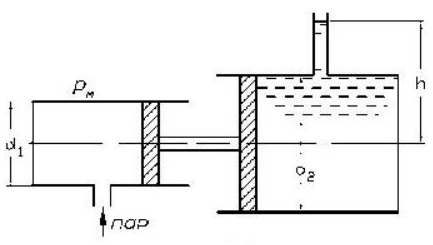



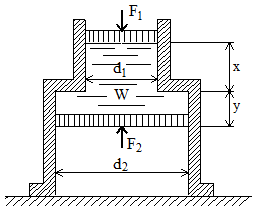









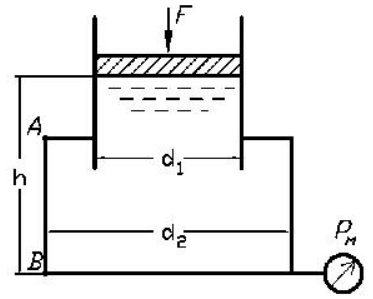

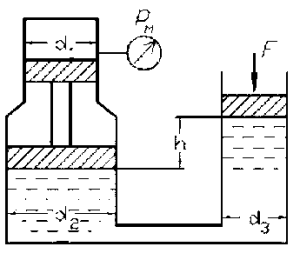














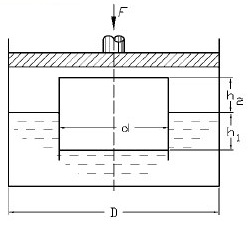




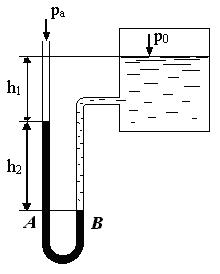





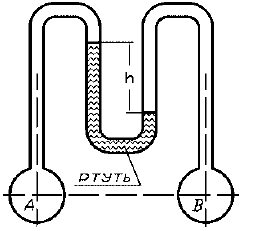


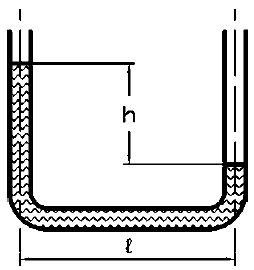












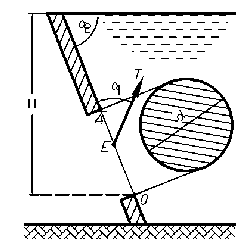
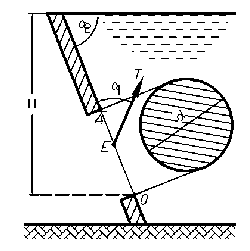

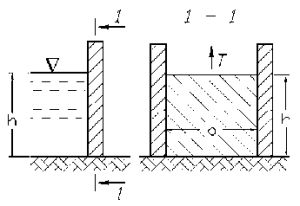
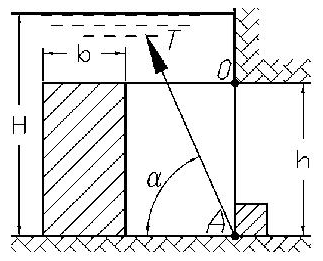

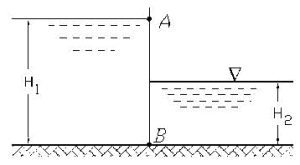





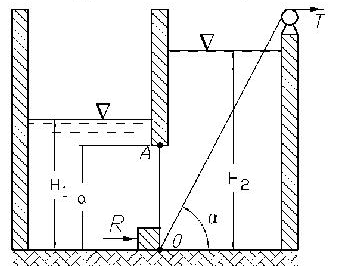

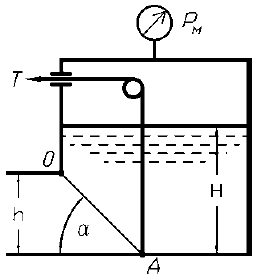



















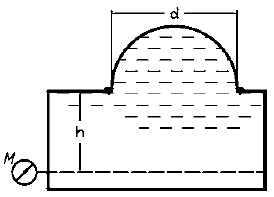



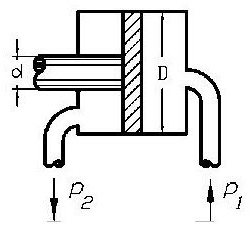

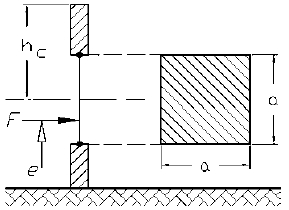



















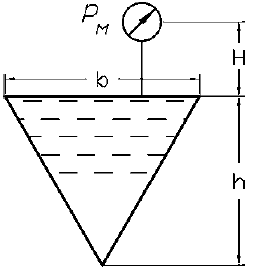


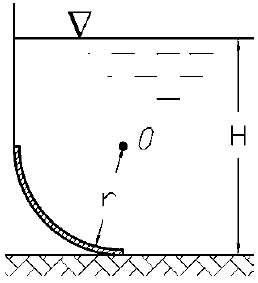






















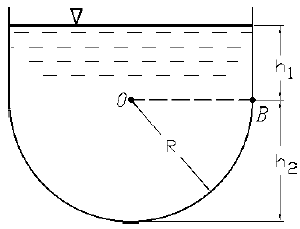


















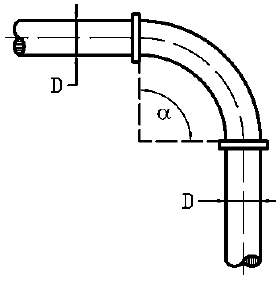






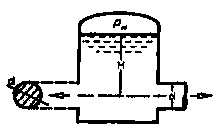



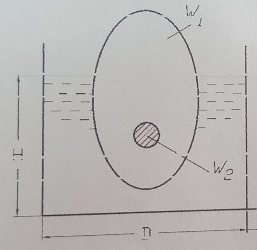








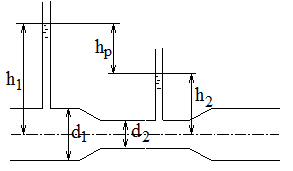

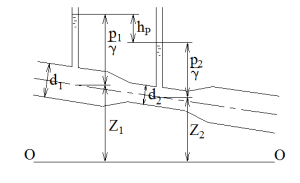




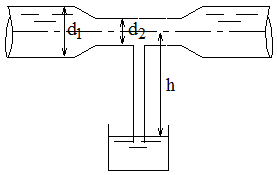





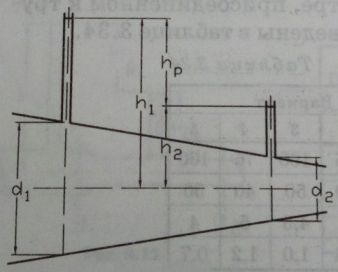
















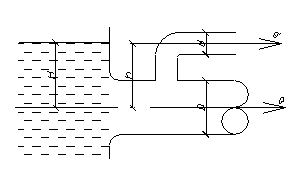





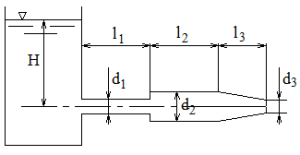



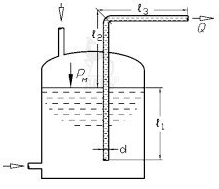




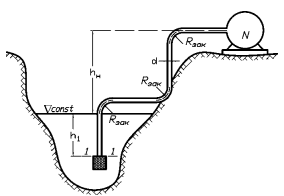


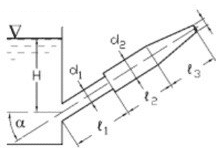









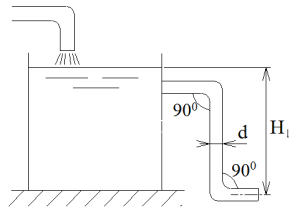




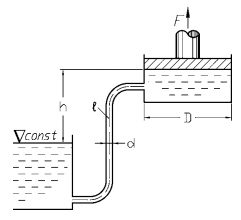

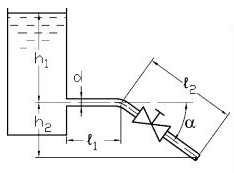
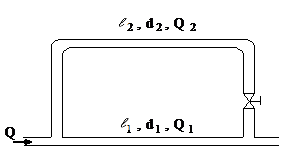


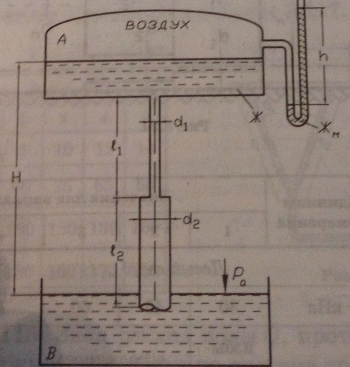







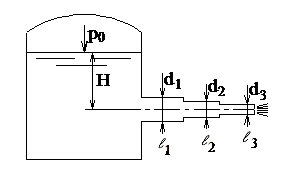


























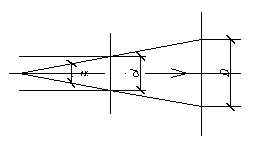




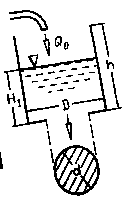




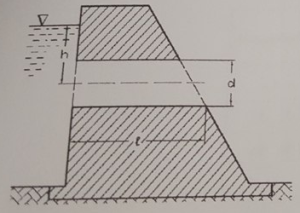



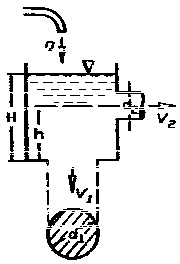




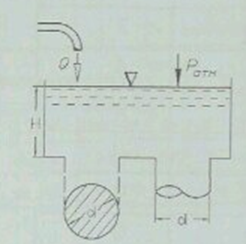













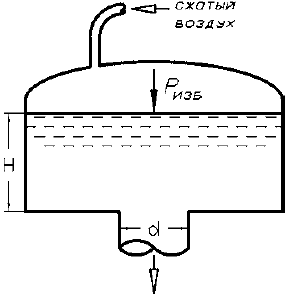













Здравствуйте, Алина! Помощь онлайн ТОЛЬКО по предварительной записи
Здравствуйте, нужна задача 2.104 срочно через полчаса
Здравствуйте, Елизавета!
Ответил Вам на почту
Здравствуйте, сколько будет стоить задача 3-147?
Анна, какие номера вариантов Вас интересуют?
Здравствуйте! Сколько будет стоить задача 2.50,2.100,3.47,3.89 и схема 32 гидростатика?
Здравствуйте, Никита! Написал Вам на почту на счет цены
Задача 2-192 сколько будет стоить?
Здравствуйте, dracculla!
ответил Вам на почту
Здравствуйте, сколько будет стоить задача 2.50, 2.183, 3.18, 3.93?
Здравствуйте, Юля! Уточните, какая задача 17?
Как получить ответ на задачу 17? Какая цена и можно ли это сделать до завтра?
Здравствуйте, Нина! Ответил Вам на почту
Здравствуйте, а можно узнать цену задачи 2-28? Заранее благодарю)
Здравствуйте, Виктория! Ответил Вам на почту
Здравствуйте, сколько будет стоить задача 2.97?