РМ.МСХ.5
Есть готовые решения этих задач, контакты
Задача 3
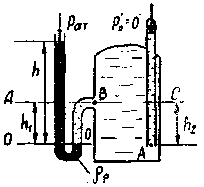
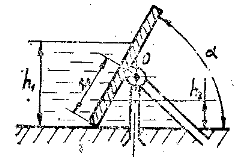
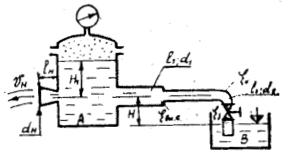
Определить абсолютное гидростатическое давление в точке А закрытого резервуара с водой (рис. 1.3), если высота столба ртути в трубке дифманометра h, а линия раздела между ртутью и водой расположена ниже точки В на величину h1, точка В – выше точки А на величину h2. Атмосферное давление pат = 98,1 кПа, удельный вес воды γв = 9,81 кН/м3, удельный вес ртути γр = 133,4 кН/м3.
Задача 5
Определить высоту подъема жидкости в пьезометре hх, если высота столба ртути в трубке дифманометра h1, а точка А расположена на глубине h2 от свободной поверхности (рис. 1.5). Атмосферное давление pатм = 98,1 кПа, удельный вес воды γв = 9,81 кН/м3.
Задача 6
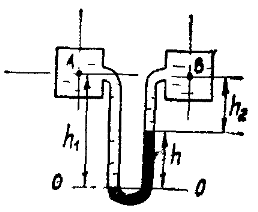
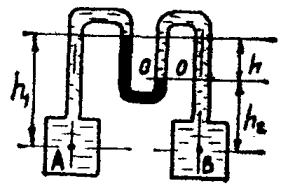
К двум резервуарам А и В, заполненным водой, присоединен дифференциальный ртутный манометр (рис. 1.6). Составить уравнение равновесия относительно плоскости равного давления и определить разность давлений в резервуарах А и В, если расстояние от оси резервуара до мениска ртути равны h1 и h2. Удельный вес воды γв = 9,81 кН/м3, удельный вес ртути γр = 133,4 кН/м3.
Задача 7
Определить разность показаний ртутного дифманометра hx, составив уравнение равновесия относительно плоскости равного давления. Дифманометр подключен к двум закрытым резервуарам с водой (рис. 1.7), давление в резервуаре А равно pА, а в резервуаре В – pВ. Удельный вес воды γв = 9,81 кН/м3, удельный вес ртути γр = 133,4 кН/м3.
Задача 8
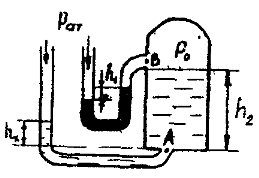
Резервуары А и В частично заполнены водой разной плотности и газом, причем к резервуару А подключен баллон с газом (рис. 1.8). Какое необходимо создать давление p0 в баллоне, чтобы получить давление pВ на свободной поверхности в резервуаре В, если высота столба ртути в трубке дифманометра h, а расстоянии от оси резервуаров до мениска ртути равны h1 и h2? Удельный вес ртути γр = 133,4 кН/м3, плотность воды в резервуаре А – ρА = 998 кг/м3, в резервуаре В – ρВ = 1029 кг/м3.
Задача 9
К двум резервуарам А и В, заполненным нефтью, присоединен дифференциальный ртутный манометр (рис. 1.9). Определить разность давлений в точках А и В, составив уравнение равновесия относительно плоскости равного давления. Разность показаний манометра h1 – h2 = h. Удельный вес ртути γр = 133,4 кН/м3, нефти – γн = 8,83 кН/м3.
Задача 10
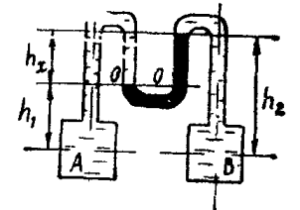
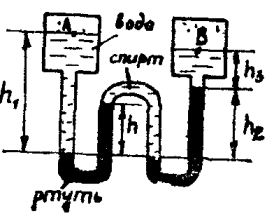
Резервуары А и В частично заполнены водой и газом (рис. 1.10). Определить избыточное давление газа на поверхности воды закрытого резервуара В, если избыточное давление на поверхности воды в закрытом резервуаре А равно pА, разность уровней ртути в двухколенном дифманометре h, мениск ртути в левой трубке манометра ниже уровня воды на величину h1, в правой трубке – h3 = 0,25h1, высота подъема ртути в правой трубке манометра h2. Пространство между уровнями ртути в манометре заполнено этиловым спиртом. Удельный вес ртути γр = 133,4 кН/м3, воды γв = 9,81 кН/м3, этилового спирта γс = 7,74 кН/м3.
Задача 11
Определить сжимающее усилие P1 гидравлического пресса с диаметрами поршней D и d (рис. 2.1), используемого для получения виноградного сока, если к малому поршню приложена сила P.
Задача 12
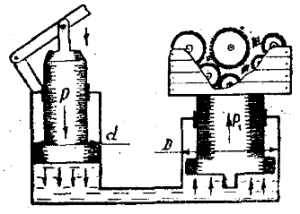
При ремонте сельскохозяйственных машин и оборудования широко используется гидравлический домкрат, принципиальная схема которого приведена на рис. 2.2. Определить усилие P, которое необходимо приложить к малому поршню, чтобы поднять груз весом G. Диаметрами поршней D и d.
Задача 15
Два сообщающихся цилиндра наполнены жидкостью (рис. 2.5). В меньший цилиндр диаметром d заключен поршень весом G. На какой высоте H установится уровень жидкости в большом цилиндре, когда вся система придет в равновесие (трением пренебречь)? Удельный вес жидкости γ = 9,81 кН/м3.
Задача 18
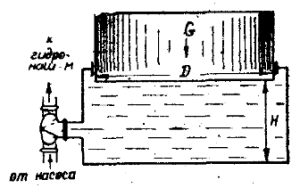
Для накопления энергии используется грузовой гидравлический аккумулятор (рис. 2.8), вес плунжера которого равен G, диаметр – D. Определить запасаемую аккумулятором энергию при ходе плунжера H = 6 м.
Задача 19
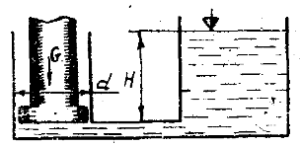
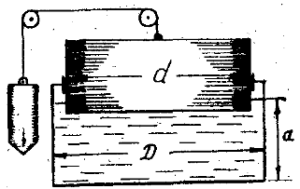
Цилиндрический резервуар с водой диаметром D и весом G висит на плунжере диаметром d (рис. 2.9). Сосуд заполнен водой на высоту a = 0,5 м. К поршню через блоки подвешен груз, удерживающий систему в равновесии. Определить вакуум в сосуде, обеспечивающий равновесие цилиндра. Трением в системе пренебречь.
Задача 20
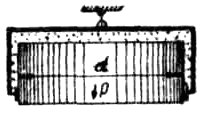
Плунжер диаметром d и весом G висит на цилиндрическом сосуде, заполненном воздухом (рис. 2.10). Определить вакуум в сосуде, обеспечивающий равновесие плунжера. Трением в системе пренебречь.
Задача 21
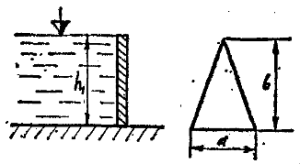
Шлюзовое окно закрыто щитом треугольной формы, ширина которого a, высота b, (рис. 3.1). За щитом воды нет, а глубина воды перед ним h1, при этом горизонт воды перед щитом совпадает с его вершиной. Определить силу абсолютного гидростатического давления и положение центра давления на щит. Удельный вес воды γв = 9,81 кН/м3.
Задача 22
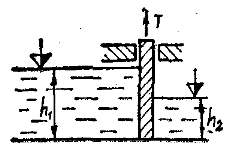
Плоский квадратный щит шириной установлен с углом наклона к горизонту α (рис. 3.2). Глубина воды перед щитом – h1, за щитом – h2, ширина щита – b. Определить силу избыточного гидростатического давления и центр давления жидкости на щит. Удельный вес воды γв = 9,81 кН/м3.
Задача 25
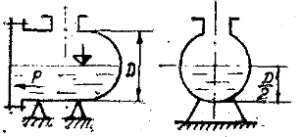
Цистерна диаметром D наполовину заполнена керосином (рис. 3.5). Определить силу избыточного гидростатического давления P, которую необходимо приложить для открытия крышки А цистерны, а также найти координату точки приложения этой силы. Плотность керосина ρк = 830 кг/м3.
Задача 26
Отверстие шлюза-регулятора (рис. 3.6) перекрыто плоским металлическим затвором с размерами: высота a, ширина b и толщина c = 0,25b. Глубина воды слева от затвора h1, а справа – h2. Определить начальную силу тяги, необходимую для открытия затвора, равнодействующую силы давления воды на затвор и положение центра ее приложения. Коэффициент трения скольжения f = 0,4, удельный вес материала, из которого изготовлен затвор, γз = 11 кН/м3, удельный вес воды γв = 9,81 кН/м3.
Задача 29
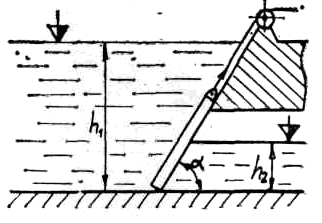
Для создания подпора в реке применяется плотина Шануана (рис. 3.9), представляющая собой плоский прямоугольный щит, который может вращаться вокруг горизонтальной оси О. Угол наклона щита α, глубина воды перед щитом h1, а за щитом — h2. Определить положение оси вращения щита (х0), при котором в случае увеличения верхнего уровня воды выше плотины, щит опрокидывался бы под ее давлением.
Задача 31
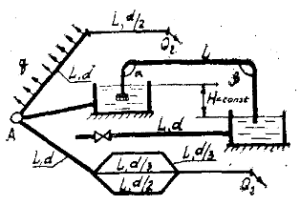
От пункта А (рис. 4.1) проложена водопроводная сеть с последовательным и параллельным соединением стальных бывших в эксплуатации трубопроводов, на которой расположены два водоема на разных отметках с постоянной разницей уровней H. Вода подается из одного водоема в другой посредством сифона, выполненного из стального трубопровода диаметром d. От нижнего водоема отходит стальной трубопровод, заканчивающий задвижкой. На последнем участке последовательного соединения трубопроводов имеется равномерно распределенный путевой объемный расход q.
Требуется:
- Определить объемный расход в сифоне с углами поворота α и β.
- Определить распределение объемного расхода воды Q1 в параллельных ветвях водопровода.
- Определить потери напора по длине трубопровода на участках последовательного соединения, если объемный расход в конце трубопровода Q2.
- Определить повышение давления Δp в трубопроводе длиной L и диаметром d при внезапном закрытии задвижки.
Задача 33
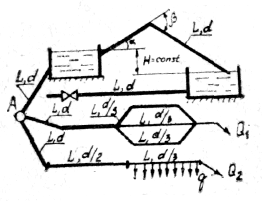
В тепличном комбинате стальные трубопроводы для подачи питательного раствора (кинематическую вязкость ν принять равной 0,01 см2/с) разветвляются на три участка: последовательный с объемным расходом Q2, параллельный с объемным расходом Q1 и участок с объемным расходом Q, в конце которого установлена задвижка (рис. 4.3). Резервуары с питательным раствором сообщаются посредством сифона с углами поворота α и β. Движение в сифоне происходит с разностью напоров – Н. Последовательные и параллельные участки трубопроводов имеют длину L, диаметры d, d/2, d/3, d/4. На одном из участков имеется путевой объемный расход q.
Требуется:
- Определить повышение давления Δр в стальном трубопроводе длиной L, с толщиной e и объемным расходом Q.
- Определить распределение расхода в параллельных ветвях участка.
- Определить объемный расход в сифоне Qсиф.
- Определить потери напора h1, h2, h3 на последовательных участках трубопровода, имеющего объемный расход Q2.
Задача 36
Водораспределительная сеть, выполненная из чугунных трубопроводов, состоит из последовательных и параллельных участков, двух резервуаров, сообщающихся при помощи сифона, и отходящего от нижнего резервуара чугунного трубопровода с задвижкой (рис. 4.6). Один из последовательных участков имеет путевой объемный расход q. Горизонты уровней в резервуарах разнятся на величину H. Сифонный трубопровод с углами поворота α и β имеет обратный клапан с сеткой и пропускает объемный расход Qсиф.
Требуется:
- Определить распределение объемного расхода Q1 в трубопроводах при параллельном соединении.
- Определить диаметр сифона.
- Определить потери напора по длине последовательно соединенных участков трубопровода, пропускающего объемный расход Q2.
- Определить начальную скорость V0 в чугунном трубопроводе с толщиной стенок e, если после внезапного закрытия задвижки давление перед задвижкой будет p, а перед закрытием давление было p0.
Задача 38
Из водоисточника А (рис. 4.8) вода подается в накопительный резервуар, где поддерживается постоянный уровень. Из резервуара-накопителя вода поступает в приемный резервуар при помощи стального сифонного водопровода, имеющего углы поворота α и β. Стальной трубопровод диаметром d, отходящий от нижнего резервуара, заканчивается задвижкой. Система последовательно соединенных трубопроводов с длиной L и диаметрами d, d/2, d/3, d/4 пропускает транзитом из источника А объемный расход Q2 к потребителю. Система трубопроводов с параллельными ветвями заканчивается последовательным участком с равномерно распределенным путевым объемным расходом q.
Требуется:
- Определить повышение давления Δp в трубопроводе диаметрами d, длиной L, имеющем толщину стенок e, при внезапном закрытии задвижки, если объемный расход составляет Q.
- Определить диаметр сифона, пропускающего объемный расход Qсиф.
- Определить распределение расхода в трубопроводах с параллельным соединением.
- Определить потери напора на участках трубопровода при последовательном соединении.
Задача 42
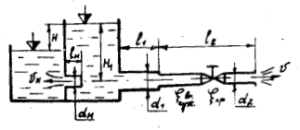
К открытому резервуару подсоединены короткий стальной трубопровод, состоящий из двух участков длиной l1 и l2, диаметрами d1 и d2 и внутренний цилиндрический насадок (насадок Борда) диаметром dн и длиной lн = 5dн (рис. 5.2). Истечение по короткому трубопроводу происходит в атмосферу под постоянным напором H1, коэффициент сопротивления крана принять равным ξкр = 3.
Определить:
- Скорость и расход воды, вытекающей из трубопровода при температуре воды t = 10 °C.
- Расход через насадок при разности уровней в резервуарах H, если коэффициент расхода насадка μн = 0,71.
- Сравнить расход воды через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.
Задача 43
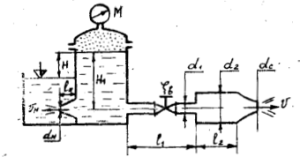
К закрытому резервуару, на свободной поверхности которого действует манометрическое давление pм, подсоединены чугунный трубопровод переменного сечения с диаметрами d1, d2 заканчивающимся соплом диаметром dс = d1, и конически сходящийся насадок с диаметром выходного сечения dн и длиной lн = 5dн. Трубопровод и насадок подсоединены на глубине H1. На первом участке длиной l1 установлен вентиль, коэффициент сопротивления которого ζв = 4. Длина второго участка l2. Коэффициент сопротивления сопла ζс = 0,06, сжатие струи на выходе из сопла отсутствует (рис. 5.3).
Определить:
- Скорость истечения V и расход Q вытекающий из сопла воды при температуре t = +10 °С и постоянном напоре H1.
- Расход воды через затопленный насадок при разности уровней в резервуарах H, если коэффициент расхода насадка μн = 0,94.
- Сравнить расход воды, проходящий через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.
Задача 44
Истечение происходит из открытого резервуара при постоянном напоре воды H1 по короткому трубопроводу переменного поперечного сечения с диаметрами d1 и d2 в атмосферу и из конически расходящегося насадка с диаметром выходного сечения dн и длиной lн = 5dн под уровень (рис. 5.4). Разность уровней – H2 = 1,5 м.
На втором участке трубопровода имеются два колена с плавным поворотом, коэффициент сопротивления каждого ξк = 0,15, и задвижки, коэффициент сопротивления которой ξз = 8,0. Коэффициент гидравлического трения на первом участке длиной l1 принять равным λ1 = 0,04, на втором участке длиной l2 – λ2 = 0,025.
Определить:
- Скорость истечения V2 и расход Q2 через трубопровод.
- Скорость истечения и расход через затопленный конически расходящийся насадок, если коэффициент скорости и коэффициент расхода насадка равны и составляют φн = μн = 0,45.
- Сравнить скорость и расход через насадок со скоростью и расходом через отверстие в тонкой стенке того же диаметра. Коэффициент скорости для отверстия φ = 0,97, а коэффициент расхода μ = 0,62.
Задача 45
Из открытого резервуара по короткому стальному трубопроводу постоянного поперечного сечения d1 и длиной l1, который заканчивается соплом диаметром dс = 0,5d1, вытекает вода при t = +30 °C в атмосферу. Истечение происходит под напором H1 (рис. 5.5). Коэффициент сопротивления крана принять равным ξк = 2,5. С другой стороны к резервуару подсоединен коноидальный насадок диаметром выходного сопла dн и длиной lн = 5dн.
Определить:
- Скорость истечения из сопла Vс и расход воды по короткому трубопроводу Qс.
- Расход воды через затопленный коноидальный насадок при разности уровней в резервуарах H, если коэффициент расхода насадка μ = 0,97.
- Сравнить расход воды через насадок с расходом через отверстие в тонкой стенке того же диаметра. Коэффициент расхода для отверстия μ = 0,62.
Задача 47
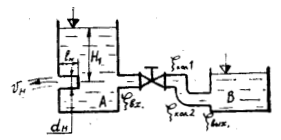
Вода при температуре t = 20 °C из резервуара А подается в резервуар В со скоростью V = 0,5 м/с по стальному трубопроводу диаметром d1 и длиной l1. Уровень воды в баке А поддерживается постоянным. Коэффициенты сопротивления: входа в трубу ζвх = 0,5; крана ζкр = 1,5; колена без закругления ζкол1 = 0,25; колена с закруглением ζкол2 = 0,14. На глубине H1 к резервуару подсоединен внутренний цилиндрический насадок (насадок Борда) диаметром dн и длиной lн = 5dн (рис. 5.7).
Определить:
- Время заполнения водой резервуара В объемом Wв = 1,15 м3 и потери напора в трубопроводе.
- Скорость истечения воды из насадка, если коэффициент скорости для насадка φн = 0,71.
- Сравнить скорость истечения из насадка со скоростью истечения из отверстия в тонкой стенке того же диаметра, если φот = 0,62.
Задача 49
Из резервуара А, на свободной поверхности которого избыточное давление pм, вода температурой t = 15 °C поступает в резервуар В по трубопроводу переменного сечения, состоящему из двух участков длиной l1 и l2 и диаметрами d1 и d2. Разность уровней в резервуарах h = H1 – H (рис. 5.9).
На глубине H1 к резервуару А подсоединен конически расходящийся насадок с диаметром выходного сечения dн и длиной lн = 5dн.
Определить:
- Режим течения, скорость V и расход воды Q, поступающей с резервуар В по трубопроводу, если коэффициент потерь на вход в трубу ξвх = 0,5, коэффициент сопротивления колена ξк = 0,4, коэффициент сопротивления полностью открытой задвижки ξз = 5, коэффициент гидравлического трения на первом участке λ1 = 0,025, на втором – λ2 = 0,04. Скоростным напором и изменением уровня в резервуаре А пренебречь.
- Скорость и расход воды через конически расходящийся насадок, если коэффициенты φн и μн равны и составляют 0,45.
- Сравнить скорость и расход, проходящий через насадок, со скоростью и расходом через отверстие в тонкой стенке, если φотв = 0,97, а μотв = 0,62.
Есть готовые решения этих задач, контакты