Механизация сельского хозяйства

РМ.МСХ.1

Решение задач по гидравлике

Задачи можно купить или заказать новые обратившись по e-mail (skype)

Задача 3

Определить абсолютное гидростатическое давление в точке А закрытого резервуара с дистиллированной водой, если при атмосферном давлении p_ат высота столба ртути в трубке дифманометра h, а линия раздела между ртутью и водой расположена ниже точки В на величину h₁. Точка В – выше точки А на величину h₂ (рис 11, схема 3).

Задача 4

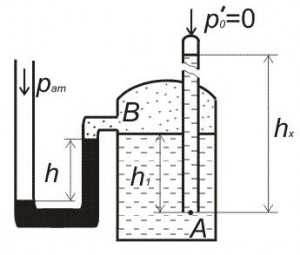
Закрытый резервуар снабжен дифманометром, установленным в точке В, и пьезометром. Определить высоту h_x поднятия пресной воды в закрытом пьезометре (соответствующую абсолютному гидростатическому давлению в точке А), если при атмосферном давлении p_ат высота столба ртути в трубке дифференциального манометра h, а точка А расположена на глубине h₁ от свободной поверхности (рис. 11, схема 4).

Задача 7

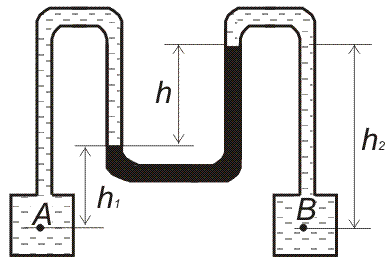
Дифференциальный ртутный манометр подключен к двум закрытым резервуарам с пресной водой. Давление в резервуаре А равно p_А. Определить давление p_В в резервуаре В, составив уравнение равновесия относительно плоскости равного давления. Определить разность показания ртутного дифманометра h (рис. 11, схема 7).

Задача 8

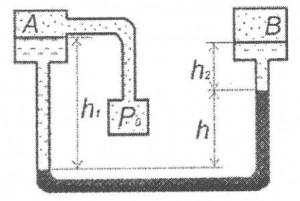
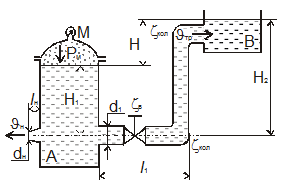
Резервуары А и В частично заполнены водой разной плотности (ρ_А и ρ_В соответственно) и газом. К резервуару А подключен баллон с газом. Высота столба ртути в трубке дифманометра h, а расстояния от оси резервуаров до мениска ртути равны h₁ и h₂ (рис. 11, схема 8). Какое необходимо создать давление p₀ в баллоне, чтобы получить давление p_В на свободной поверхности в резервуаре В?

Купить задачу 8 вариант 40

Задача 9

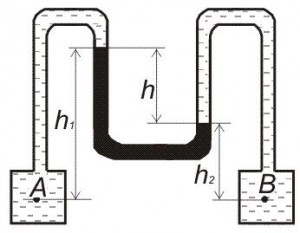
К двум резервуарам А и В заполненным нефтью, присоединен дифференциальный ртутный манометр. Определить разность давлений в точках А и В, составив уравнение равновесия относительно плоскости равного давления. Разность уровней жидкости в дифференциальном манометре h (рис. 11, схема 9)

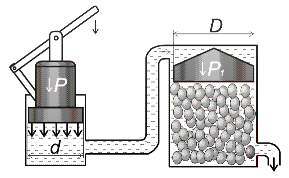
Задача 11

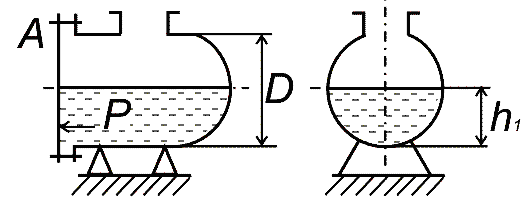
Гидравлический пресс с диаметрами поршней D и d используется для получения виноградного сока. К малому поршню приложена сила P (рис. 12, схема 1). Определить сжимающее усилие P₁ большого поршня, если коэффициент полезного действия (КПД) гидравлического пресса η = 0,8.

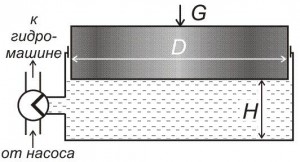
Задача 18

Для накопления энергии используется грузовой гидравлический аккумулятор с диаметром плунжера D, вес которого G и ход H (рис. 12, схема 8). Определить запасаемую аккумулятором энергию, если КПД аккумулятора η = 0,85.

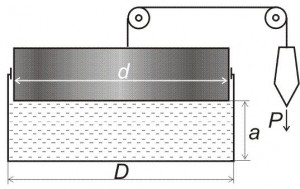
Задача 19

Цилиндрический резервуар диаметром D и весом G, заполненный водой на высоту a, висит на поршне диаметром d. К поршню через блоки подвешен груз, удерживающий систему в равновесии (рис. 12, схема 9). Определить вакуум в сосуде, обеспечивающий равновесие в цилиндре. Трением пренебречь.

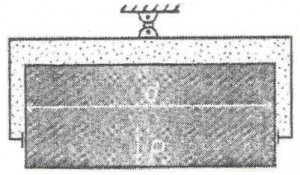
Задача 20

На цилиндрическом сосуде, заполненном воздухом, висит плунжер диаметром d и весом G (рис. 12, схема 10). Определить вакуум в сосуде, обеспечивающий равновесие плунжера. Трением в системе пренебречь.

Купить задачу 20 вариант 96

Задача 21

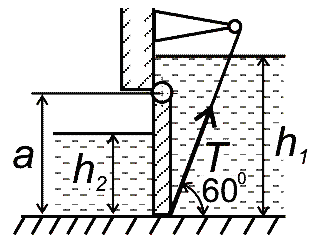
Прямоугольный поворотный щит размером a × b закрывает выпускное отверстие плотины. Справа от щита уровень воды h₁, слева – h₂. Определить начальную силу Т натяжения тросов, необходимую для открытия щита, пренебрегая трением в цапфах (рис. 13, схема 1).

Задача 22

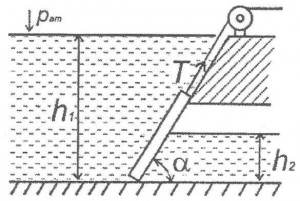
Плоский квадратный щит шириной a установлен с углом наклона к горизонту α. Глубина воды перед щитом – h₁, за щитом h₂. Определить силу абсолютного гидростатического давления и положение центра давления жидкости на щит (рис. 13, схема 2).

Купить задачу 22 вариант 107

Задача 23

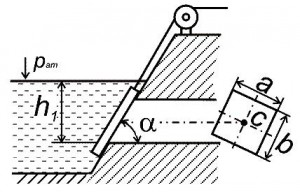
Для сброса излишков воды используется донный водовыпуск, прямоугольный затвор которого имеет размеры a и b, угол наклона α. Глубина воды от ее свободной поверхности до нижней кромки затвора h₁. Определить силу избыточного гидростатического давления жидкости на затвор водовыпуска и положение центра давления (рис. 13, схема 3).

Задача 25

Цистерна диаметром D заполнена керосином плотностью ρ_к на глубину h₁. Определить силу избыточного гидростатического давления P, которая приложена к крышке А цистерны, а также найти координату точки приложения этой силы (рис. 13, схема 5).

Задача 27

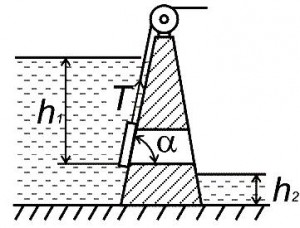
Прямоугольный щит высотой a, шириной b, толщиной c = 0,25b, весом G, с углом наклона α перекрывает отверстие в теле плотины. Нижняя кромка щита находится в воде на глубине h₁, коэффициент трения скольжения в направляющих f. Определить силу тяги T, которая необходима для поднятия щита вверх (рис. 13, схема 7).

Задача 30

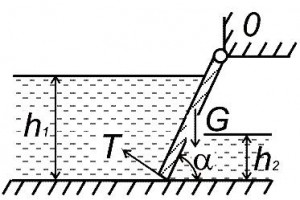
Ирригационный канал перегораживается плоским квадратным щитом шириной a, весом G, с углом наклона a. Глубина воды перед щитом h₁, a уровень воды за ним h₂. Определить, пренебрегая трением в шарнире, начальную силу тяги T, которую необходимо приложить для подъема щита (рис. 13, схема 10).

Задача 31

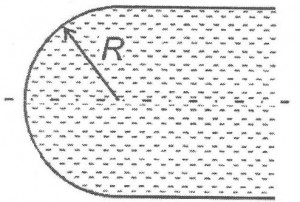
Определить срезающие и разрывающие усилия в боковой сферической стенке цистерны, заполненной водой, если радиус сферы равен R (рис. 14, схема 1).

Купить задачу 31 вариант 154

Задача 33

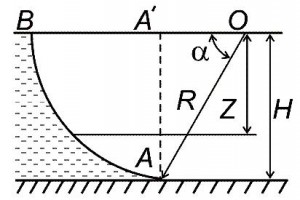
Определить величину силы P и центр давления воды на сегментальный затвор, имеющий ширину b и радиус R, если центральный угол сектора равен α. Уровень воды перед затвором расположен на высоте H (рис. 14, схема 3).

Задача 36

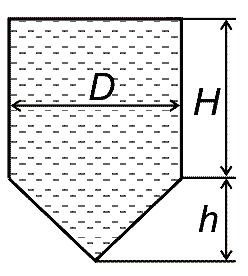
Открытый резервуар диаметром D заполнен морской водой. Определить силу P_z, отрывающую коническое днище, и силу P_x, разрывающую листы днища по образующей резервуара. Высота цилиндрической части H, высота конуса h (рис. 14, схема 6).

Задача 37

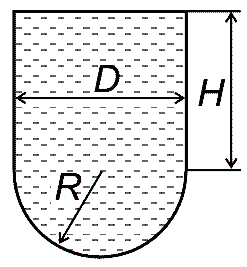
Цилиндрический резервуар диаметром D имеет дно в виде полусферы. Верхняя часть имеет высоту H, а нижняя радиус R. Вычислить силу давления нефти P_z на дно резервуара. Определить силу P_x разрывающую резервуар по образующей (рис. 14, схема 7).

Задача 39

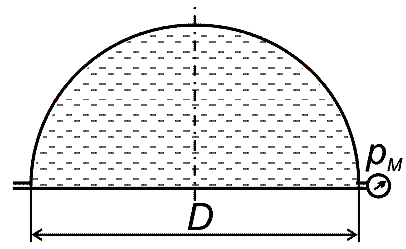
Купол, имеющий форму полусферы, испытывает манометрическое давление p_м. Определить силу, которая стремится поднять купол, если его диаметр равен D (рис. 14, схема 9).

Задача 40

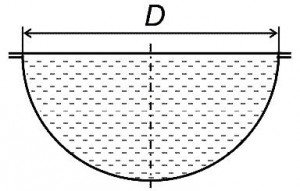
Определить величины сил P_x и P_y давления воды на полусферическое днище сосуда диаметром D (рис. 14, схема 10).

Задача 201

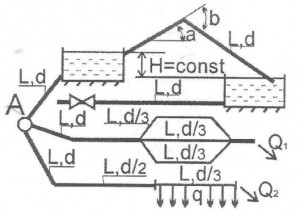
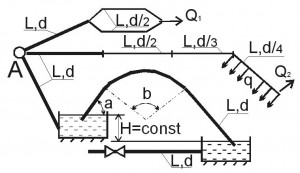
(Рис. 25, схема 1). От пункта А проложена водопроводная сеть: с последовательным и параллельным соединениями стальных, бывших в эксплуатации, трубопроводов, к двум водоемам на разных отметках и постоянной разницей уровней Н. Вода подается из одного водоема в другой посредством сифона с углами поворота α и β, выполненного из стального трубопровода диаметром d. От нижнего водоема отходит стальной трубопровод длиной L и диаметром d, заканчивающийся задвижкой. На последнем участке последовательного соединения трубопроводов имеется равномерно распределенный путевой объемный расход q и объемный расход в конце трубопровода Q₂.

Определить: 1. Объемный расход в сифоне. 2. Распределение объемного расхода воды Q₁ в параллельных ветвях водопровода. 3. Потери напора по длине трубопровода на участках последовательного соединения. 4. Повышение давления Δp в трубопроводе при внезапном закрытии задвижки.

Купить задачу 201

Задача 202

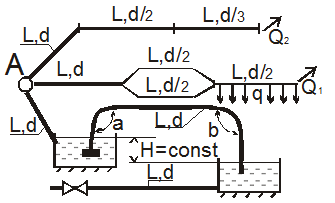
(Рис. 25, схема 2). Из источника А вода подается в разветвленную сеть. Магистральный трубопровод имеет последовательные участки с объемным расходом Q₂, длиной L, диаметрами d, d/2, d/3 и параллельные ветви с объемным расходом Q₁, имеющие диаметры d/2. На одном из участков имеется путевой объемный расход воды q. По ответвлению вода подается в резервуар, который связан посредством сифонного трубопровода с другим резервуаром. Разница уровней в резервуарах Н. Сифонный трубопровод выполнен с углами поворота α и β, имеет сетку с обратным клапаном. От нижнего резервуара отходит чугунный трубопровод с толщиной стенок е, в котором перед закрытием задвижки имеется давление p₀, а давление при мгновенном закрытии задвижки возрастает до p.

Определить: 1. Распределение расхода в ветвях водопровода на параллельных участках. 2. Потери напора на последовательных учатках трубопровода. 3. Начальную скорость υ₀ движения воды в чугунном трубопроводе с задвижкой. 4. Диаметр сифона.

Задача 204

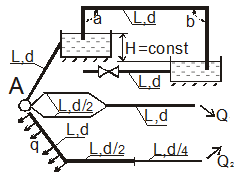
(Рис. 25, схема 4). Из пункта А вода подается по чугунному трубопроводу в открытые емкости с разницей между верхней и нижней отметками – Н. Емкости сообщаются посредством сифона с объемным расходом Q_сиф, выполненного из чугунных труб с углами поворота α и β. Трубопровод с объемным расходом Q₂ состоит из последовательных участков каждый длиной L и диаметрами d, d/2, d/4. Параллельный участок состоит из двух ветвей каждая длиной L и диаметром d/2.От нижней емкости отходит чугунный трубопровод с толщиной стенок е и диаметром d, заканчивающийся задвижкой. Начальное избыточное давление в трубопроводе – р₀, начальная скорость – V₀.

Определить:

1. Потери напора по длине трубопровода при последовательном соединении.

2. Распределение расхода Q₁ в трубопроводе на участках с параллельным соединением.

3. Напряжение σ при внезапном закрытии трубопровода.

4. Диаметр сифона.

Задача 206.

(Рис. 25, схема 6). Водопроводная сеть, выполненная из чугунных трубопроводов с толщиной стенок e, состоит из последовательных и параллельных участков, двух резервуаров, сообщающихся при помощи сифона, и отходящего от нижнего резервуара чугунного трубопровода с объемным расходом Q₂ с задвижкой. Один из последовательных участков имеет путевой объемный расход q. Горизонты уровней в резервуарах разнятся на величину H. Сифонный трубопровод с углами поворота a и b имеет обратный клапан с сеткой и пропускает объемный расход Q_сиф. Перед закрытием задвижки давление Р₀, после мгновенного закрытия задвижки давление перед задвижкой Р.

Определить: 1. Распределение объемного расхода Q_i в трубопроводах при параллельном соединении. 2. Диаметр сифона. 3. Потери напора по длине последовательно соединенных участков трубопровода. 4. Определить начальную скорость u₀ в чугунном трубопроводе.

Задача 207.

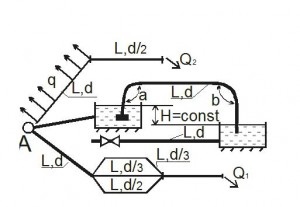
(Рис. 25, схема 7). Два бассейна сообщаются чугунным сифоном, имеющим обратный клапан с сеткой с углами поворотов a и b. Отметки уровней воды отличаются на величину H. От нижнего бассейна отходит бетонная труба диаметром d, длиной L, с объемным расходом Q, с задвижкой. Магистральные асбестоцементные трубопроводы имеют последовательные и параллельные участки. Объемный расход в трубопроводе с параллельными участками – Q₁, с последовательным соединением участков – Q₂. На конечном участке последовательного соединения происходит равномерная путевая раздача q.

Определить: 1. Распределение расхода по параллельным ветвям. 2. Потери напора на последовательных участках. 3. Повышение давления Dp в трубопроводе при внезапном закрытии задвижки. 4. Объемный расход в сифоне Q_сиф.

Задача 211

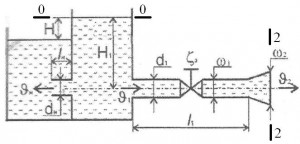
(Рис. 26, схема 1). Из открытого резервуара при постоянном напоре H₁ воды температурой t = 50 °С вытекает с одной стороны в атмосферу по короткому трубопроводу диаметром d₁ и длиной l₁ с шероховатостью стенок Δ = 1 мм, задвижкой, коэффициент сопротивления которой ζ_з и на конце диффузором ζ_диф = 0,9, площадь живого сечения которого за расширением S₂ = 2S₁, с другой стороны вода подается в другой резервуар через затопленный внешний цилиндрический насадок (насадок Вентури). Разность уровней между ними Н. Насадок имеет диаметр d_н, длину l_н = 5d_н и коэффициент расхода насадка μ_н.

Определить: 1. Скорость истечения V₂, расход воды Q₂ и коэффициент гидравлического трения λ по короткому трубопроводу. 2. Расход через насадок Q_н.

Купить задачу 211

Задача 214

(Рис. 26, схема 4). Истечение происходит из открытого резервуара в атмосферу при постоянном напоре воды H₁ по короткому трубопроводу переменного поперечного сечения с диаметрами d₁ и d₂ и длинами l₁ и l₂, для которых коэффициенты гидравлического трения соответственно равны λ₁ и λ₂. На втором участке трубопровода имеются два колена с плавным поворотом и понижением трубопровода на H₂ = 1,5 м и задвижка, коэффициент сопротивления каждого поворота ξ_к, коэффициент сопротивления задвижки ξ_з. Истечение из конически расходящегося насадка с диаметром выходного сечения d_н и длиной l_н = 5d_н происходит под уровень при постоянной разности уровней H. Коэффициент скорости и коэффициент расхода насадка равны φ_н = μ_н.

Определить:

1. Скорость истечения V_тр и расход Q_тр через короткий трубопровод.

2. Скорость истечения V_н и расход Q_н через затопленный конически расходящийся насадок.

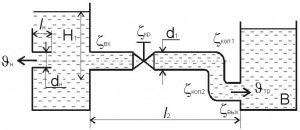
Задача 217

(Рис. 26, схема 7). Вода при температуре t = 20 °C из резервуара А подается в резервуар В со скоростью V = 0,5 м/с по стальному трубопроводу диаметром d₁ и длиной l₁. Уровень воды в баке А поддерживается постоянным H₁. Коэффициенты сопротивления: входа в трубу ξ_вх; крана ξ_кр; колена без закругления ξ_кол1; колена с закруглением ξ_кол2. На глубине H₁ к резервуару подсоединен внутренний цилиндрический насадок (насадок Борда) диаметром d_н и длиной l_н = 5d_н при коэффициенте скорости для насадка φ_н.

Определить:

1. Время заполнения водой резервуара В объемом W_в = 1,15 м³ и потери напора в трубопроводе.

2. Скорость истечения воды из насадка V_н.

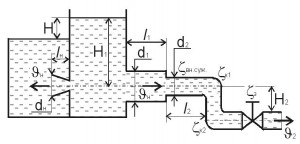
Задача 218

(Рис. 26, схема 8). Из резервуара А, заполненного водой на высоту H, и находящегося под манометрическим давлением p_м, вода подается в резервуар В на высоту H₂ = H₁ + H по стальному трубопроводу длиной l₁ и диаметром d₁, с коленом и задвижкой, коэффициент сопротивления задвижки ξ_з; каждого колена с закруглением ξ_кол при коэффициенте гидравлического трения λ₁. К резервуару А на глубине H₁ подсоединен конический сходящийся насадок с диаметром выходного сечения d_н и длиной l_н = 5d_н, истечение из которого происходит в атмосферу с коэффициентами расхода μ_н и скорости φ_н. Кинематическая вязкость воды ν = 1,24 · 10^-6 м²/с. Скоростным напором и изменением уровня в резервуаре А пренебречь.

Определить:

1. Режим течения, расход Q_тр и скорость V_тр протекающей по трубопроводу воды.

2. Скорость V_н и расход Q_н проходящей через конический сходящийся насадок.

Задачи можно купить обратившись по e-mail (skype)