РАрх.3
Часть задач есть решенные, контакты
Пример 1.1
В отопительной системе (котел, радиаторы, трубопроводы) частного дома содержится V = 0,3 м3 воды. Сколько воды дополнительно войдет в расширительный бак при нагревании от 20 до 80°С.
Пример 1.2
В отопительный котел поступает 50 м3воды при температуре t1 = 70°С. Какой объем V воды будет выходить из котла при нагреве воды до t2 = 90°С.
Пример 1.3
Определить среднюю толщину δ известковых отложений в герметичном водоводе внутренним диаметром d = 0,3 м и длиной l = 2 км. При выпуске воды в количестве ΔV=0,05 м3 давление в водоводе падает на величину Δp = 106 Па. Считать, что отложения по диаметру и длине водовода распределены равномерно.
Задача 1.1
Определить плотность жидкости ρ, полученной смешиванием объема жидкости V1 = 0,02 м3 плотностью ρ1 = 910 кг/м3 и объема жидкости V2 = 0,03 м3 плотностью ρ2 = 850 кг/м3.
Задача 1.2
Определить плотность топливной смеси (по весу) при следующем составе: керосин (ρк = 775 кг/м3) – 40%, мазут (ρм = 870 кг/м3) – 60%.
Задача 1.3
При гидравлическом испытании трубопровода длиной L = 1000 м и диаметром d = 100 мм давление поднималось от p1 = 1 МПа до p2 = 1,5 МПа.
Определить объем жидкости ΔV, который был дополнительно закачан в водопровод. Коэффициент объемного сжатия βP = 4,75·10-10 1/Па.
Задача 1.4
При гидравлическом испытании трубопровода диаметром d = 0,4 м длиной L = 20 м и давление воды сначала было p1 = 5,5 МПа. Через час давление упало до p2 = 5,0 МПа. Определить, пренебрегая деформацией трубопровода, сколько воды вытекло при этом через неплотности. Коэффициент объемного сжатия βP = 4,75·10-10 1/Па.
Стоимость: 90 руб
Задача 1.5
Как изменится объем воды в системе отопления, имеющей вместимость V = 100 м3, после подогрева воды от начальной температуры t1 = 15 °C до t2 = 95 °C. Коэффициент температурного расширения βt = 0,00072 1/°С.
Задача 1.6
Трубопровод диаметром d = 500 мм и длиной L = 1000 м наполнен водой при давлении p1 = 400 кПа, и температуре воды t1 = 5 °C.
Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до t2 = 15 °C, если коэффициент объемного сжатия βP = 5,18·10-10 1/Па, а коэффициент температурного расширения βt = 150·10-6 1/°С.
Задача 1.7
Определить повышение давления, при котором начальный объем воды уменьшится на 3%. Коэффициент объемного сжатия воды βP = 4,75·10-10 1/Па.
Задача 1.8
При гидравлических испытаниях (проверке герметичности) подземного трубопровода длиной L = 500 м, диаметром d = 0,1 м давление в нем повысилось от от p1 = 0 до p2 = 1,0 МПа. Пренебрегая деформацией стенок трубопровода, определить объем воды, которую необходимо дополнительно закачать в трубопровод. Объемный модуль упругости воды принять равным Е = 2000 МПа.
Задача В.9
В трубопровод вместимостью 50 м3 во время испытаний было дополнительно закачано 0,05 м3 воды. Определить приращение давления в трубопроводе, если объемный модуль упругости воды Е = 2·109 Па.
Задача В.10
Винтовой плунжерный насос для тарировки манометров работает на масле с коэффициентом объемного сжатия βр = 0,625·10-9 1/Па. Определить на сколько оборотов надо повернуть маховик винта, чтобы поднять давление внутри насоса на Δp = 0,1 МПа, если объем рабочей камеры пресса V = 628 см3, диаметр плунжера d = 20 мм, шаг винта h = 2 мм. Стенки рабочей камеры считать недеформируемыми.
Задача 1.11
Резервуар заполнен жидкостью, объем которой V = 8 м3. Определить коэффициент температурного расширения жидкости βt, если при увеличении температуры от t1 = 10 °С до t2 = 20 °С объем жидкости увеличился на 6 л.
Задача 1.12
В отопительный котел поступает объем воды V = 80 м3 при температуре t1 = 60 °С. Какой объем воды V1 будет выходить из котла при нагреве воды до температуры t2 = 90 °С.
Задача 1.13
Для периодического аккумулирования дополнительного объема воды, получающегося при изменении температуры, к системе водяного отопления в верхней ее точке присоединяют расширительные резервуары, сообщающиеся с атмосферой. Определить наименьший объем расширительного резервуара, чтобы он полностью не опоражнивался. Допустимое колебание температуры воды во время перерывов в топке Δt = 30 °C. Объем воды в системе V = 0,7 м3. Коэффициент температурного расширения воды при средней температуре t = 80 °С βt = 6·10-4 1/°С.
Задача 1.14
Определить среднюю толщину отложений в герметичном водоводе внутренним диаметром d = 0,5 м и длиной l = 3 км. При выпуске воды объемом ΔV = 0,08 м3 давление в водоводе падает на Δр = 1 МПа. Отложения по диаметру и длине водовода распределены равномерно. Коэффициент объемного сжатия воды сжатия βр = 5·10-10 1/Па.
Задача 1.15
Стальной водовод диаметром d = 0,4 м и длиной l = 1 км, проложенный открыто, находится под давлением р = 2 МПа при температуре воды t1 = 10 °С. Определить давление воды в водоводе при повышении температуры до t2 = 15 °С в результате наружного прогрева.
Задача 1.16
Определить изменение плотности воды при увеличении давления от p1 = 100 кПа до p2 = 10000 кПа. При изменении давления температура воды не изменяется, коэффициент объемного сжатия βр = 5·10-10 1/Па.
Задача 1.17
В отопительной системе дома содержится V = 0,4 м3 воды при температуре t1 = 15°C. Определить объем воды, который дополнительно войдет в расширительный бачок при повышении температуры до t2 = 90°С.
Задача 1.18
Определить изменение плотности воды при изменении температуры от t1 = 5 °С до t2 = 95 °С.
Задача 1.19
Вязкость нефти, определенная вискозиметром, составила 4°Е, а ее плотность ρ =880 кг/м3. Определить кинематический и динамический коэффициенты вязкости нефти.
Задача 1.20
Определить ротационным вискозиметром вязкость жидкости плотностью ρ = 920 кг/м3. Вес груза G = 80 Н, диаметры цилиндра Dц = 225 мм, 12 барабана Dб = 223 мм, шкива d = 200 мм. Глубина погружения барабана в жидкость lб = 250 мм. Время опускания груза tгр = 12 с, путь lгр = 300 мм.
Пример 2.1
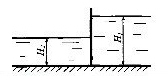
Определить давление в резервуаре p0 и высоту подъема уровня воды h1 в трубке 1, если показания ртутного манометра h2=0,15 м и h3=0,8 м.
Пример 2.1
Определить силу преобразования F, развиваемую гидравлическим прессом, у которого диаметр большего плунжера D = 500 мм, меньшего d = 50 мм, высота Н = 1 м. Рабочая жидкость с плотностью ρ = 850 кг/м3. К рычагу приложено усилие R = 250 Н. Отношение плеч рычага равно а/в =12.
Задача 2.1
Определить избыточное и абсолютное давления в точке, расположенной на дне открытого резервуара, если уровень жидкости в резервуаре h = 2 м, а плотность жидкости ρ = 1000 кг/м3. Атмосферное давление ра = 0,1 МПа.
Задача 2.2
Определить высоту наполнения резервуара жидкостью с относительной плотностью δ = 0,85, если в точке, расположенной на дне открытого резервуара, абсолютное давление рабс = 135 кПа. Атмосферное давление ра = 0,1 МПа (см. рис. к зад. 2.1).
Задача 2.3
Определить абсолютное и избыточное давление в точке А, расположенной на глубине h = 1,5 м, если плотность жидкости ρ = 800 кг/м3. Атмосферное давление ра = 750 мм рт.ст.
Стоимость: 90 руб
Задача 2.4
Определить абсолютное и избыточное давление в точке С под поршнем и в точке b на глубине h = 2 м, если диаметр поршня d = 0,2 м, а сила, действующая на поршень, Р = 3 кН. Плотность жидкости ρ = 850 кг/м3.
Задача 2.5
Определить абсолютное давление р0 в закрытом резервуаре, если в трубке, присоединенной к резервуару, ртуть поднялась на h = 0,2 м. Атмосферное давление ра = 0,1 МПа, плотность ртути ρрт = 13600 кг/м3.
Задача 2.6
Определить при каком значении вакуумметрического давления р0вак в закрытом резервуаре жидкость поднимается на высоту h = 0,5 м, плотность жидкости ρ = 1100 кг/м3, атмосферное давление ра = 0,1 МПа.
Задача 2.7
На какую высоту h поднимется ртуть в трубке, присоединенной к закрытому резервуару, вакуумметрическое давление в котором р0вак = 0,6·105 Па. Плотность ртути ρрт = 13600 кг/м3.
Задача 2.8
Определить избыточное давление р0н в закрытом резервуаре при условии: h1 = 0,6 м, плотность жидкости ρ = 900 кг/м3. Атмосферное давление ра = 0,1 МПа. Чему равно абсолютное давление на дно резервуара при h2 = 1,0 м. Построить эпюру избыточного давления на боковую поверхность резервуара.
Задача 2.9
В U-образную трубку налиты ртуть и вода. Определить h, если hрт = 80 мм; плотность ртути ρрт = 13600 кг/м3, воды – ρв = 1000 кг/м3 .
Задача 2.10
При измерении уровня жидкости в резервуаре барботажным методом по трубке продувают воздух. Показания манометра рм = 75 кПа. Определить уровень жидкости в резервуаре Н. Относительная плотность жидкости δ = 0,86, h = 0,2 м.
Задача 2.11
Определить манометрическое давление в трубопроводе А, если высота столба ртути
по пьезометру h2 = 25 см. Центр трубопровода расположен на h2 = 40 см ниже линии раздела между водой и ртутью.
Задача 2.12
Абсолютное давление в трубопроводе В рв = 1,5·105 Па. Определить избыточное давление в трубопроводе С, если оба трубопровода заполнены водой, а показания
дифференциального ртутного манометра h = 20 см (ρрт = 13600 кг/м3).
Задача 2.13
Определить разность давлений в трубопроводах В и С, если оба трубопровода заполнены водой, а показания дифференциального ртутного манометра h = 320 мм (ρрт = 13600 кг/м3).
Задача 2.14
Вакуумметрическое давление в трубопроводе В рв = 25 кПа. Определить абсолютное и избыточное давление в трубопроводе С, если трубопровод В заполнен жидкостью с относительной плотностью δ =1,18, трубопровод С – водой. Показания дифференциального ртутного манометра h = 0,25 м, Н = 0,85.
Задача 2.15
Определить избыточное давление воды в трубе по показаниям батарейного ртутного
манометра. Отметки уровней от оси трубы z1 = 1,75 м, z2 = 3 м, z3 = 1,5 м, z4 = 2,5 м. Плотность ртути ρрт = 13600 кг/м3, воды — ρв = 1000 кг/м3.
Задача 2.16
Для опрессовки водой подземного трубопровода (проверки на герметичность) применяется ручной поршневой насос. Определить объем воды (Е = 2000 МПа), который нужно накачать в трубопровод для повышения избыточного давления в нем от 0 до 1,0 МПа. Длина трубопровода L = 500 м, диаметр – d = 100 мм. Чему равно усилие на рукоятке насоса в последний момент опрессовки, если диаметр поршня насоса dн = 40 мм, а соотношение плеч рычажного механизма а/b = 5?
Задача 2.17
Определить абсолютное давление в точке А и вес груза G, лежащего на поршне 2, если для его подъема к поршню 1 приложена сила F = 500 Н. Диаметры поршней D = 300 мм, d = 80 мм. Высота Н = 1,5 м. Плотность масла ρм = 850 кг/м3.
Задача 2.18
Определить силу, прижимающую всасывающий клапан диаметром D2 = 150 мм к седлу, имеющему диаметр D3 = 80 мм, если диаметр насосного цилиндра D1 = 250 мм, а усилие, действующее на шток, Р = 500 Н. Седло клапана расположено ниже оси цилиндра на h1 = 0,9 м и выше свободной поверхности жидкости на h2 = 4,5 м, причем труба под клапаном заполнена водой.
Задача 2.19
Паровой прямодействующий насос подает воду на высоту H = 50 м. Каково рабочее давление пара, если диаметр парового цилиндра D = 200 мм и d = 100 мм? Давление на поршнях со стороны штоков считать атмосферным.
Задача 2.20
Определить силу F, которую необходимо приложить к штоку поршня для удержания в равновесии, если мановакууметр показывает давление выше атмосферного ризб = 35 кПа. Диаметр поршня d = 150 мм, высота Н = 1,85 м, плотность жидкости ρ = 920 кг/м3.
Пример 3.1
Две вертикальные трубы центрального отопления соединены горизонтальным участком, на котором установлена задвижка диаметром d = 0,2 м. Температура воды в правой вертикальной трубе 80°С, а в левой 20°С. Найти разность сил суммарного давления на задвижку справа Fпр и слева Fл. Высота воды в вертикальных трубах над уровнем горизонтальной трубы h = 20 м.
Пример 3.2
Щит, перекрываемый канал, расположен под углом α = 45° к горизонту и закреплен шарнирно к опоре над водой. Определить усилие, которое необходимо приложить к тросу для открывания щита, если ширина щита b = 2 м, глубина воды перед щитом h1 = 2,5 м, а после щита h2 = 1,5 м. Шарнир расположен над высоким уровнем воды на расстоянии h3 = 1 м. Весом щита и трением в шарнире можно пренебречь.
Пример 3.3
Определить силу суммарного давления на секторный затвор и ее направление. Глубина воды перед затвором H = 4 м, длина затвора L = 8 м, угол α = 60°.
Задача 3.1
Определить силу гидростатического давления и центр давления воды на прямоугольный затвор шириной b = 1,2 м, закрывающий вход в прямоугольную трубу, высота которой h = 0,8 м. Глубинажидкости в резервуаре H = 3,5 м, а = 0,5 м.
Задача 3.2
Определить силу гидростатического давления жидкости на круглую крышку колодца диаметром D = 1,2 м. Относительная плотность жидкости δ = 1,25, глубины H1 = 4,5 м, H2 = 1,0 м.
Задача 3.3
Определить силу и центр давления воды на стенку шириной b = 15 м, глубина воды h = 3 м.
Стоимость: 180 руб
Задача 3.4
Определить равнодействующую силу и центр давления воды на наклонную прямоугольную стенку шириной b = 10 м, если глубина воды H1 = 6 м, H2 = 2 м, а угол наклона стенки α = 60°.
Стоимость: 250 руб
Задача 3.5
Прямоугольное отверстие высотой h = 0,4 м и шириной b = 1 м в вертикальной стенке открытого резервуара с водой закрыто щитом. Определить силу и центр давления воды на щит, если Н = 1,3 м.
Задача 3.6
Определить равнодействующую силу и центр давления воды на прямоугольную стенку шириной b = 10 м, если глубины воды Н1 = 5 м, Н2 = 3 м.
Стоимость: 150 руб
Задача 3.7
В вертикальной стенке имеется отверстие, перекрываемое щитом в виде равностороннего треугольника, сторона которого b = 1,5 м. Определить силу гидростатического давления и положение центра давления, если H = 2,3 м.
Задача 3.8
В вертикальной стенке имеется отверстие, перекрываемое щитом в форме эллипса с размерами а = 1,5 м, b = 2,5 м. Определить силу гидростатического давления и положение центра давления, если H = 0,3 м.
Задача 3.9
В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается равносторонним треугольным щитом со стороной b = 1,5 м. Определить силу гидростатического давления и положение центра давления, если H = 2,3 м, избыточное давление в резервуаре р0изб = 5 кПа.
Задача 3.10
В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса с размерами а = 1,5 м, b = 2,5 м.
Определить силу гидростатического давления и положение центра давления, если H = 3,2 м, вакуумметрическое давление в резервуаре р0вак = 10 кПа.
Задача 3.11
Цилиндрический резервуар для хранения мазута диаметром D = 4 м имеем полусферическую крышку и сообщается с атмосферой через трубу диаметром d = 0,2 м. Определить вертикальную составляющую силы гидростатического давления мазута на крышку, если Н1 = 4 м, Н2 = 8 м, а плотность мазута ρ = 890 кг/м3.
Задача 3.12
Построить тело давления и определить силу, открывающую полусферическую крышку диаметром d = 1 м, Н = 2 м.
Задача 3.13
Построить тело давления и определить силу, прижимающую коническую крышку диаметром d = 1,2 м к основанию резервуара. Резервуар заполнен водой, глубина воды Н = 3 м, высота крышки h = 1 м.
Задача 3.14
Определить величину и направление силы давления воды на боковую поверхность цилиндрического затвора диаметром d = 1,6 м и длиной l = 4 м. Глубина воды Н = 3 м.
Задача 3.15
Построить тело давления и определить величину и направление силы гидростатического давления жидкости с относительной плотностью δ = 1,25 на затвор. Затвор является частью цилиндра радиусом R = 2,6 м, глубина жидкости в резервуаре Н = 3,8 м.
Задача 3.16
На щите, наклоненном к горизонту на угол α = 60°, имеется отверстие, которое перекрывается круглой крышкой диаметром d = 0,8 м. Определить силу гидростатического давления и центр давления воды на крышку люка, а = 1,0 м.
Задача 3.17
В вертикальной стенке имеется отверстие, перекрываемое щитом в виде равностороннего треугольника, сторона которого b = 2,5 м. Определить силу гидростатического давления и положение центра давления, если H = 3,4 м.
Задача 3.18
В боковой вертикальной стенке резервуара имеется отверстие, которое перекрывается щитом в форме эллипса с размерами а = 1,5 м, b = 2,5 м.
Определить силу гидростатического давления и положение центра давления, если H = 0,3 м, вакуумметрическое давление в резервуаре р0вак = 20 кПа.
Задача 3.19
Построить тело давления и определить силу, прижимающую полусферическую крышку диаметром d = 1,2 м к основанию резервуара. Резервуар заполнен водой, глубина воды Н = 3 м.
Задача 3.20
Построить тело давления и определить величину и направление силы гидростатического давления жидкости с относительной плотностью δ = 0,8, действующей на цилиндрическую поверхность, если радиус и длина образующей цилиндра соответственно R = 1,2 м, b = 0,5 м.
Пример 4.1
Определить пределы изменения гидравлического радиуса R для канализационных самотечных трубопроводов, если их диаметр d изменяется от 150 до 3500 мм. Расчетное наполнение принять: a = h/d = 0,6 для труб диаметром d = 150 мм; a = h/d = 0,8 для труб диаметром d = 3500 мм.
Пример 4.2
Определить режим движения воды в водопроводной трубе диаметром d = 300 мм, если протекающий по ней расход Q = 0,136 м3/с. Температура воды 10°С.
Задача 4.1
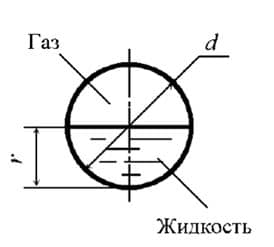
Жидкость движется в лотке со скоростью V = 0,1 м/с. Глубина наполнения лотка h = 30 см, ширина по верху В = 50 см, ширина по низу b = 20 см. Определить смоченный периметр, площадь живого сечения, гидравлический радиус, расход, режим движения жидкости, если динамический коэффициент вязкости жидкости μ = 0,0015 Па·с, а ее плотность ρ = 1200 кг/м3.
Задача 4.2
Найти минимальный диаметр d напорного трубопровода, при котором нефть будет двигаться при турбулентном режиме, если кинематический коэффициент вязкости нефти ν = 0,3 см2/с, а расход в трубопроводе Q = 8 л/с.
Задача 4.3
По трубе диаметром d = 0,1 м под напором движется вода. Определить расход, при котором турбулентный режим сменится ламинарным, если температура воды t = 25°C.
Стоимость: 90 руб
Задача 4.4
Определить критическую скорость, при которой происходит переход от ламинарного режима к турбулентному, в трубопроводе диаметром d = 30 мм при движении воды (ν = 0,009 Ст), воздуха (ν = 0,162 Ст) и глицерина (ν = 4,1 Ст).
Стоимость: 90 руб
Задача 4.5
Определить, изменится ли режим движения воды в напорном трубопроводе d = 0,5 м при возрастании температуры от 15 до 65°С, если расход в трубопроводе Q = 15 л/с.
Задача 4.6
Вода движется под напором в трубопроводе прямоугольного сечения. Определить, при каком максимальном расходе сохранится ламинарный режим. Температура воды t = 30 °С, а = 0,2 м, b = 0,3 м.
Стоимость: 90 руб
Задача 4.7
По трубе диаметром d = 0,1 м под напором движется вода. Определить расход, при котором турбулентный режим сменится ламинарным, если температура воды t = 25°C.
Задача 4.8
Жидкость движется в безнапорном трубопроводе с расходом Q = 22 м3/ч. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 80 мм. Определить, при какой температуре будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости представлен на рисунке.
Стоимость: 150 руб
Задача 4.9
Жидкость, имеющая динамический коэффициент вязкости μ = 1,005 Па·с и плотность ρ = 900 кг/м3, движется в трапецеидальном лотке. Определить критическую скорость, при которой будет происходить смена режимов движения жидкости. Глубина наполнения h = 0,2 м, ширина лотка по дну b = 25 см, угол наклона боковых стенок лотка к горизонту α = 30°.
Задача 4.10
Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d = 12 мм и максимальный диаметр d = 3500 мм. Расчетные скорости движения воды в них V = 0,5÷4 м/с. Определить минимальное и максимальное значение чисел Рейнольдса и режим течения в этих трубопроводах.
Задача 4.11
Для осветления сточных вод используют горизонтальный отстойник, представляющий собой удлиненный прямоугольный резервуар. Его глубина h = 2,6 м, ширина b = 5,9 м. Температура воды t = 20°С. Определить среднюю скорость и режим движения сточной жидкости, если ее расход Q = 0,08 м3/с, а коэффициент кинематической вязкости ν = 1,2·10-6 м2/с. При какой скорости в отстойнике будет наблюдаться ламинарный режим движения жидкости?
Задача 4.12
Конденсатор паровой турбины оборудован 8186 трубками диаметром d = 2,5 см. Через трубки пропускается охлаждающая вода при t = 10°С. Будет ли при расходе воды Q = 13600 м3/с обеспечен турбулентный режим движения в трубках?
Задача 4.13
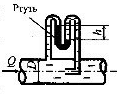
Определить режим движения горячей воды (t = 80°С) в пробковом кране, проходное сечение которого при частичном открытии изображено на рисунке, если l = 20 мм, b = r = 3 мм, расход воды Q = 0,1 л/с.
Задача 4.14
Определить режим движения воды при t = 20°С в смесителе, проходное сечение которого открыто наполовину, если d = 10 мм, расход воды Q = 0,1 л/с.
Задача 4.15
Смазка протекает через кольцевую щель. Определить гидравлический радиус при условии, что D = 50 мм, d = 48 мм.
Задача 4.16
Определить гидравлический радиус для формы потока, изображенной на рисунке.
Задача 4.17
Определить гидравлический радиус, если простая задвижка на трубе круглого сечения d частично закрыта, = 0,5.
Задача 4.18
Построить эпюру скоростей и касательных напряжений в сечении трубы диаметром d = 50 мм, если расход потока Q = 100 см3/с, а температура воды t = 8°С.
Задача 4.19
Определить максимальную и среднюю в сечении скорости, построить эпюру скоростей потока нефти в трубе диаметром d = 400 мм, если расход потока Q = 15 л/с, коэффициент кинематической вязкости ν = 0,29 см2/с.
Задача 4.20
Построить эпюру осредненных скоростей в сечении трубы, по которой протекает поток бензина с расходом Q = 60 л/с, если диаметр трубы d = 350 мм, кинематический коэффициент вязкости ν = 0,0093 Ст. Гидравлический коэффициент трения λ = 0,03.
Пример 5.1
На оси водопроводной трубы установлена трубка Пито с дифференциальным ртутным манометром. Определить максимальную скорость движения воды в трубе Vmax, если разность уровней ртути в манометре Δh = 18 мм.
Пример 5.2
Горизонтальная труба диаметром d = 5 см соединяет резервуары с водой, в которых поддерживаются постоянные уровни Н1 = 4,5 м и H2 = 2,5 м. Для регулирования расхода на трубопроводе установлен вентиль. Определить коэффициент сопротивления вентиля и потерю напора в нем, если расход воды Q = 12,5 л/с, а избыточное давление на поверхности воды в напорном баке ризб = 25 кПа. Другими потерями напора пренебречь.
Задача 5.1
Из напорного бака вода течет по трубе диаметром d1 = 20 мм и затем вытекает в атмосферу через брандспойт с диаметром выходного отверстия d2 = 10 мм.
Избыточное давление воздуха в баке р0 = 0,18 МПа; высота Н = 1,6 м. Пренебрегая потерями энергии, определить скорость течения воды в трубе V1 и на выходе из насадка V2.
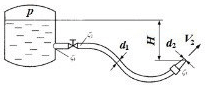
Задача 5.2
Определить скорость движения бензина V и расход Q в сифонном трубопроводе. Нижняя точка оси трубопровода расположена ниже уровня жидкости в питающем резервуаре на расстоянии h = 2,5 м. Внутренний диаметртрубопровода d = 25 мм, плотность бензина ρ = 850 кг/м3. Потерями напора пренебречь.
Задача 5.3
Определить расход жидкости Ж, вытекающей из бака по трубопроводу диаметром d, если избыточное давление воздуха в баке р0, высота уровня Н0, высота подъема жидкости в пьезометре, открытом в атмосферу Н. Потерями энергии пренебречь.
Стоимость: 90 руб
Задача 5.4
Вода движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление больше в сечении 1-1 Δр = 25 кПа. Определить расход Q, если внутренний диаметр трубопровода в сечении 1-1 D = 65 мм, а в сечении 2-2 d = 40 мм, разность отметок сечений Δz = 2 м. Потерями напора пренебречь.
Стоимость: 150 руб
Задача 5.5
Керосин движется в трубчатом расходомере в направлении от сечения 1-1 к 2-2. Избыточное давление в сечении 1-1 р1 = 35 кПа. Определить избыточное давление в сечении 2-2, если внутренний диаметр трубопровода в сечении 1-1 D = 50 мм, а в сечении 2-2 d = 35 мм, разность отметок сечений Δz = 1 м, расход Q = 2 л/с. Потерями напора пренебречь.
Задача 5.6
Определить расход воды в трубопроводе, если согласно показаниям ртутного дифференциального манометра h = 30 мм. Плотность ртути ρ = 13600 кг/м3, внутренний диаметр трубопровода D = 80 мм. Потери напора не учитывать.
Стоимость: 120 руб
Задача 5.7
По горизонтальной трубе переменного сечения протекает нефть с расходом Q = 1,3 л/с. Определить разность показаний пьезометров h, если диаметр трубопровода в широком сечении D = 10 см, а в узком d = 5 см. Плотность нефти ρ = 850 кг/м3. Потерями напора пренебречь.
Задача 5.8
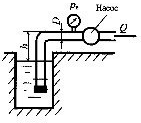
Насос с подачей Q = 7,2 м3/ч забирает воду из колодца. Определить наибольший вакуум рвак при входе в насос. Внутренний диаметр трубопровода D = 80 мм, высота установки насоса над уровнем жидкости h = 4 м. Потери напора Δh = 0,5 м.
Стоимость: 120 руб
Задача 5.9
По трубопроводу диаметром D = 150 мм движется вода с расходом 20 л/мин. Определить, пренебрегая потерями напора, разность уровней в жидкостном манометре. Плотность жидкости в манометре ρ = 1300 кг/м3.
Задача 5.10
Нефть движется под напором в трубопроводе квадратного сечения. Определить критическую скорость, при которой будет происходить смена режимов движения жидкости, если сторона квадрата a = 0,05 м, динамический коэффициент вязкости μ = 0,02 Па·с, а плотность нефти ρ = 850 кг/м3.
Задача 5.11
По горизонтальному трубопроводу переменного сечения движется нефть, плотность которой ρ = 850 кг/м3. Диаметр в широком сечении трубопровода d1 =50 мм. Расход жидкости в трубопроводе Q = 0,5 л/с, разность уровней в дифференциальном манометре, заполненном ртутью плотностью ρ = 13600кг/м3, составляет h = 35 мм. Определить диаметр трубопровода в узком сечении. Потерями напора пренебречь.
Задача 5.12
Определить скорость и расход газа с плотностью ρ = 20 кг/м3 в трубопроводе с внутренним диаметром D = 50 мм. В колене манометра находится жидкость плотностью ρж = 1000 кг/м3. Потери напора не учитывать.
Задача 5.13
По горизонтальному трубопроводу переменного сечения движется вода. Из бачка А по трубке, подведенной к трубопроводу, поступает краситель, имеющий плотность ρ = 1300 кг/м3. Определить расход воды в трубопроводе, при котором прекратится подача красителя. Уровень красителя в бачке H = 0,5 м, диаметр трубопровода в широком сечении d1 = 150 мм, в узком – d2 = 100 мм, избыточное давление воды в широком сечении трубопровода составляет 30 кПа. Потерями напора пренебречь.
Задача 5.14
Для условий задачи 4.13 определить, при какой высоте Н прекратится подача красителя. Расход воды в трубопроводе Q = 1,8 м3/мин, диаметр трубопровода в широком сечении d1 = 200 мм, в узком – d2 = 100 мм, абсолютное давление воды в широком сечении трубопровода составляет 150 кПа. Потерями напора пренебречь.
Задача 5.15
Определить давление в сечении трубопровода с диаметром d1 = 0,1 м, если вода в трубке поднялась на высоту h = 3 м, диаметр cуженой части трубопровода d2 = 0,6 м, расход воды в трубопроводе Q = 0,0065 л/с. Потери напора не учитывать.
Задача 5.16
На вертикальной водопроводной трубе постоянного диаметра на расстоянии l = 10 м установлены два манометра. Нижний манометр показывает давление 1,2 кг/см2, а верхний – 0,8 кг/см2. Определить гидравлический уклон и направление движения жидкости.
Задача 5.17
По нагнетательному патрубку диаметром d1 = 200 мм вентилятором подается воздух плотностью ρ = 1,2 кг/м3 с расходом Q = 0,8 м3/с при избыточном давлении р1 = 1 кПа. К патрубку подсоединен диффузор с диаметром выходного сечения d2 = 300 мм. Определить давление воздуха на выходе из диффузора. Изменение плотности воздуха и потери в диффузоре не учитывать.
Задача 5.18
К трубе, по которой движутся дымовые газы плотностью ρ = 0,6 кг/м3, присоединен микроманометр, заполненный спиртом (ρсп = 0,6 кг/м3). Показание шкалы манометра, наклоненной под углом α = 30° к горизонту, l = 15 мм. Определить скорость движения дымовых газов.
Задача 5.19
На вертикальной водопроводной трубе, состоящей из труб диаметром d1 = 27 мм и d2 = 15 мм, установлены два манометра. Нижний манометр показывает давление 1,6 кг/см2, а верхний – 1,2 кг/см2. Определить направление движения воды, гидравлический и пьезометрический уклоны, если расход составляет Q = 0,3 л/с.
Задача 5.20
Поршень диаметром D = 200 мм вытесняет воду по короткому трубопроводу диаметром d = 20 мм в атмосферу. Определить усилие на поршень, если скорость истечения жидкости v = 5 м/с, потери напора hw = 2 м.
Пример 6.1
Расход горячей воды с температурой 95°С через радиатор водяного отопления Q = 0,1 м3/ч. Определить потери давления между сечениями 1-1 и 2-2, если диаметр подводящих трубопроводов d = 0,0125 м, а их общая длина l = 5 м. Принять следующие коэффициенты сопротивления: для поворота ζ1 = 1,45 для крана ζ2 = 0,5, для радиатора ζ3 = 2,1.
Пример 6.2
Вода, перекачивается насосом из открытого бака А в расположенный ниже резервуар B, где поддерживается постоянное давление рв = 0,18 МПа (абс.) по трубопроводу общей длиной l = 225 м и диаметром d =250 мм. Разность уровней воды в баках h=3 м. Определить потребный напор, создаваемый насосом для подачи в бак B расхода воды Q = 98 л/с. Принять суммарный коэффициент местных сопротивлений ζ = 6,5. Эквивалентная шероховатость стенок трубопровода Δ = 0,15 мм. Жидкость – вода с плотностью ρ = 1000 кг/м3 и вязкостью ν = 0,01 Ст. Атмосферное давление ра = 0,1 МПа.
Задача 6.1
По трубопроводу, соединяющему два резервуара, в которых поддерживаются постоянные уровни, перетекает вода с плотностью ρ = 1000 кг/м3. Диаметр трубопровода d = 20 мм. В верхнем баке поддерживается избыточное давление р0изб = 15 кПа, а в нижнем — вакуумметрическое давление р0вак = 7 кПа. Разность уровней в баках H = 5 м. Определить расход жидкости, если коэффициент гидравлического трения λ = 0,028, а длина трубопровода l = 15 м. Местными потерями напора пренебречь.
Задача 6.2
Из напорного бака по наклонному трубопроводу переменного сечения движется жидкость с относительной плотностью δ = 0,85. Диаметры участков трубопровода d1 = 50 мм, d2 = 30 мм, а длина соответственно равна l1 = 80 м, l2 = 40 м. Начало трубопровода расположено выше его конца на величину z = 3,5 м. Для обоих участков трубопровода коэффициент гидравлического трения λ = 0,038. Какой уровень Н необходимо поддерживать в напорном баке, чтобы скорость движения жидкости на выходе из трубопровода была v = 1,8 м/с? Местными потерями напора пренебречь.
Задача 6.3
Вода перетекает из бака А в бак Б по трубе диаметром d = 25 мм, на которой установлены вентиль с коэффициентом сопротивления ζв = 3,5, а также диффузор с ζд = 0,5 и диаметром выходного отверстия D = 75 мм. Показание вакуумметра pвак = 10 кПа, высота Н = 2,5 м, h = 2 м. Определить расход Q c учетом всех местных сопротивлений. При решении потерями на трение пренебречь, принять коэффициент сопротивления каждого колена ζкол = 0,5, учесть потери напора на входе в трубу (внезапное сужение) и на выходе в бак (внезапное расширение). Взаимным влиянием сопротивлений пренебречь.
Стоимость: 150 руб
Задача 6.4
Для измерения расхода воды, которая подается по трубе А в бак Б установлен расходомер Вентури В. Определить максимальный расход, который можно пропустить через данный расходомер при условии отсутствия в нем кавитации, если давление насыщенных паров соответствует hн.п. = 2 мм вод.ст. Уровень воды в баке поддерживается постоянным, равным H = 1,5 м, высота расположения трубы h = 0,5 м. Размеры расходомера: d1 = 50 мм и d2 = 20 мм. Атмосферное давление принять соответствующим 760 мм рт.ст., коэффициент сопротивления диффузора ζдиф = 0,2. Учесть потери на внезапное расширение при входе в бак.
Стоимость: 150 руб
Задача 6.5
Определить расход воды, вытекающей из трубы диаметром d = 22 мм через плавное расширение (диффузор) и далее по трубе диаметром D = 28 мм в бак. Коэффициент сопротивления диффузора ξдиф = 0,2 (отнесен к скорости в трубе диаметром d), показание манометра pм = 20 кПа; высота h = 0,7 м, H = 6 м. Учесть потери на внезапное расширение, потерями на трение пренебречь, режим течения считать турбулентным.
Задача 6.6
Вода по трубе 1 подается в открытый бак. Во избежание переливания воды через край бака устроена вертикальная сливная труба 2 диаметром d = 50 мм. Определить необходимую длину L трубы 2 из условия, чтобы при Q = 10 л/с вода не переливалась через край бака. Режим течения считать турбулентным, а величинами h пренебречь (h = 0). Принять следующие коэффициенты сопротивления: на входе в трубу ζ1 = 0,5, в колене ζ2 = 0,5, на трение по длине трубы λ = 0,03.
Стоимость: 120 руб
Задача 6.7
По трубопроводу диаметром d = 50 мм насос перекачивает воду на высоту Н = 10 м. Коэффициент сопротивления вентиля ζ = 8. За какое время насос наполнит резервуар емкостью W = 40 м3, если манометр, установленный на выходе из насоса, показывает избыточное давление рм = 250 кПа. Сопротивлением трубопровода пренебречь.
Задача 6.8
Определить давление в напорном баке p, необходимое для получения скорости истечения из брандспойта V2 = 20 м/с. Длина шланга l = 20 м, диаметр d1 = 20 мм, диаметр выходного отверстия брандспойта d2 = 10 мм. Высота уровня воды в баке над отверстием брандспойта Н = 5 м. Учесть местные гидравлические сопротивления при входе в трубу ζ1 = 0,5, в кране ζ2 = 3,5, в брандспойте ζ3 = 0,1, который отнесен к скорости V2, потери на трение в трубе λ = 0,018.
Стоимость: 150 руб
Задача 6.9
Определить минимальное давление pм, измеряемое манометром перед сужением трубы, при котором будет происходить подсасывание воды из резервуара А в узком сечении трубы. Диаметры трубы d1 = 60 мм и d2 = 20 мм высота ее расположения h1 = 6 м, высота уровня жидкости в баке h2 = 1 м. Принять коэффициенты сопротивления сопла ζсоп = 0,08, диффузора ζдиф = 0,3.
Задача 6.10
Определить расход воды через сифонный трубопровод, если высота H1 = 1 м, Н2 = 2 м, Н3 = 4 м. Общая длина трубы l = 20 м, диаметр d = 20 мм. Режим течения считать турбулентным. Учесть потери на входе в трубу ζ1 = 1, в коленах ζ2 = 0,2, в вентиле ζ3 = 4, на трение в трубе λ = 0,035. Подсчитать вакуум в верхнем сечении х-х трубы, если длина участка от входа в трубу до этого сечения lх = 8 м.
Задача 6.11
Насос нагнетает воду в напорный бак, где установились постоянный уровень на высоте H = 3,5 м и постоянное давление р2 = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d1 = 80 мм, показывает p1 = 0,3 МПа. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, равен d2 = 65 мм; коэффициент сопротивления этой трубы принят равным ζ = 0,2.
Задача 6.12
Определить потребный напор, который необходимо создать в сечении 0-0 для подачи в бак воды вязкостью ν = 0,008 Ст, если длина трубопровода l = 80 м, его диаметр d = 50 мм, расход жидкости Q = 15 л/с, высота Hо = 30 м, давление в баке р2 = 0,2 МПа, коэффициент сопротивления крана ζ1 = 5, колена ζ2 = 0,8, а шероховатость стенок трубы Δ = 0,04. Потерями на расширение потока пренебречь.
Задача 6.13
Вода перетекает из бака А в резервуар Б по трубе диаметром d= 25 мм, длиной l = 10 м. Определить расход воды Q, если избыточное давление в баке р1 = 200 кПа, высота уровней Н1 = 1 м, Н2 = 5 м. Режим течения считать турбулентным. Принять следующие коэффициенты сопротивления: на входе в трубу ζ1 = 0,5, в вентиле ζ2 = 4, в коленах ζ3 = 0,2, на трение λ = 0,025. Учесть потери при выходе трубопровода в бак Б.
Задача 6.14
Определить расход в трубе для подачи воды с вязкостью ν = 0,01 Ст на высоту H = 16,5 м, если диаметр трубы d = 10 мм, ее длина l = 20 м и располагаемый напор в сечении трубы перед краном Hрасп = 20 м. При решении принять коэффициент сопротивления крана ζ1 = 4, колена ζ2 = 1, а потерями на расширение потока и скоростным напором в трубопроводе пренебречь. Трубу считать гидравлически гладкой.
Указание: Задачу решить методом последовательных приближений, задавшись коэффициентом Дарси λ, а затем, уточняя его, найти величину расхода Q с необходимой точностью.
Задача 6.15
Определить расход воды с вязкостью ν = 0,01 Ст, перетекающей через трубу из бака А в резервуар Б, если диаметр трубы d = 20 мм, ее длина l = 10 м, высота Н = 8 м. При решении принять коэффициент сопротивления крана ζ1 = 3, каждого колена ζ2 = 1, а эквивалентную шероховатость трубы Δ = 0,05 мм. Учесть потери на внезапное сужение потока при выходе из бака А и внезапное расширение при входе потока в резервуар Б.
Указание: Задачу решить методом последовательных приближений, задавшись коэффициентом Дарси λ, а затем, уточняя его.
Задача 6.16
Определить предельную высоту всасывания масла насосом при подаче Q = 0,4 л/с из условия бескавитационной работы насоса, считая, что абсолютное давление перед входом в насосе должно быть p ≥ 30 кПа. Длина и диаметр всасывающего трубопровода: l = 2 м; d = 20 мм. Плотность масла ρ = 900 кг/м3, вязкость ν = 2 Ст. Атмосферное давление 750 мм.рт.ст. Сопротивлением входного фильтра пренебречь.
Задача 6.17
При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Hрасп = 9,6 м; длина трубопровода l = 10 м; эквивалентная шероховатость Δ = 0,05 мм; давление в баке p0 = 30 кПа; высота H0 = 4 м; вязкость жидкости ν = 0,015 Ст и ее плотность ρ = 1000 кг/м3? Местными гидравлическими сопротивлениями в трубопроводе пренебречь. Учесть потери при входе в бак.
Задача 6.18
Определить максимальный расход воды Q, который можно допустить во всасывающем трубопроводе насоса из условия отсутствия кавитации перед входом в насос, если высота всасывания h = 4 м, размеры трубопровода: l = 6 м; d = 24 мм; предельное давление бензина принять рв = 40 кПа. Режим течения считать турбулентным. Коэффициент сопротивления приемного фильтра ζф = 2; коэффициент сопротивления трения λт = 0,03; h0 = 750 мм.рт.ст.; ρб = 1000 кг/м3.
Задача 6.19
Определить абсолютное давление жидкости перед входом в центробежный насос при подаче Q = 1 л/с и высоте всасывания h = 0,6 м. Всасывающую трубу, длина которой l = 7,6 м, диаметр d = 20 мм, считать гидравлически гладкой. Учесть сопротивление приемного клапана с фильтрующей сеткой ζф = 3. Вязкость жидкости ν = 0,006 Ст, ее плотность ρ = 750 кг/м3. Скоростным напором при входе в насос пренебречь. Атмосферное давление соответствует 750 мм.рт.ст.
Задача 6.20
Вода с вязкостью ν = 0,02 Ст нагнетается насосом из колодца в водонапорную башню по вертикальному трубопроводу. Определить диаметр трубы от крана К до бака d2, если высота башни Н = 10 м, глубина погружения насоса Но = 5 м, высота уровня жидкости в баке h = 1 м, длина участка трубопровода от насоса до крана ζк = 3, показание манометра рм = 0,3 МПа, а подача насоса Q = 1,5 л/с. При решении пренебречь скоростным напором на выходе из насоса, но учесть потерю скоростного напора при входе в бак. Трубы считать гидравлически гладкими.
Указание: Задачу решить методом последовательных приближений, задавшись начальным значением диаметра трубопровода d, а затем, уточняя его, найти величину d с необходимой точностью.
Пример 7.1
Вода вытекает из закрытого резервуара в атмосферу через отверстие диаметром d = 20 мм и коэффициентом расхода μ = 0,62. Глубина погружения центра отверстия h = 0,45 м, избыточное давление на поверхности жидкости p0и = 8,3 кПа. Определить расход жидкости. Как изменится избыточное давление для пропуска того же расхода, если к отверстию присоединить внешний насадок длиной l = 0,1 м.
Пример 7.2
В пароохладитель через трубку со сверлениями поступает охлаждающая вода температурой 20°С расходом Q = 0,00278 м3/с. Давление воды в трубке p1 = 106 Па, давление в корпусе пароохладителя p2 = 0,7×106 Па. Определить, сколько отверстий диаметром d = 0,003 м нужно просверлить в трубке для обеспечения заданного расхода воды.
Пример 7.3
Определить время опорожнения цистерны с мазутом при следующих данных: объем мазута в цистерне W = 50 м3; диаметр цистерны D = 2,8 м; диаметр сливного патрубка d = 0,1 м; кинематическая вязкость мазута ν = 0,69·10-4 м2/с.
Задача 7.1
Определить напор в баке, если расход воды при истечении через цилиндрический насадок диаметром d = 0,05 м составляет Q = 0,05 м3/с. Истечение происходит при постоянном напоре.
Задача 7.2
Определить расход жидкости (ρ = 800 кг/м3), вытекающей из бака через отверстие площадью S0 = 1 см2. Показание ртутного прибора, измеряющего давление воздуха, h = 268 мм, высота H0 = 2 м, коэффициент расхода отверстия μ = 0,60.
Задача 7.3
Из отверстия диаметром d = 0,4 см в тонкой стенке резервуара вытекает вода, имеющая температуру t = 18 ℃ ;. Отверстие расположено на высоте h = 8 м над поверхностью земли. Постоянный напор воды в резервуаре H = 6 м. Определить расход и скорость истечения, а также расстояния x, на котором струя коснется поверхности земли.
Задача 7.4
Жидкость плотностью ρ = 850 кг/м3 вытекает через установленный на боковой поверхности закрытого резервуара цилиндрический насадок диаметром d = 6 см. Избыточное давление на свободной поверхности жидкости pизб = 6,1 кПа, расход жидкости Q =5 л/с, глубина погружения насадка h = 90 см. Определить коэффициент расхода насадка.
Стоимость: 90 руб
Задача 7.5
Определить направление истечения жидкости (ρ = ρвод) через отверстие d0 = 5 мм и расход, если разность уровней H = 2 м, показание вакуумметра рвак соответствует 147 мм.рт.ст., показание манометра рм = 0,25 МПа, коэффициент расхода μ = 0,62.
Задача 7.6
Определить расход и скорость воды при истечении из круглого отверстия диаметром d = 0,065 м в тонкой стенке и установить, как они изменяются, если к этому отверстию присоединить цилиндрический насадок длиной l = 4d. Напор в центре тяжести отверстия H = 2,8 м.
Задача 7.7
Определить объем воды V, налитой в цилиндрический бак диаметром D = 0,8 м, если вся вода вытекла из бака через отверстия в дне диаметром d = 100 мм за время t = 60 c. Какое время t1 потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?
Задача 7.8
Определить время полного опорожнения открытого резервуара с постоянной площадью сечения Ω объемом V = 50 л через отверстие в дне при начальном расходе Q = 1,8 м3/ч и напоре H = 0,5 м.
Задача 7.9
Время частичного опорожнения вертикально расположенного цилиндрического открытого бака через донное отверстие в тонкой стенке составило t = 40 с. За это время уровень жидкости изменился от h1 = 2 м до h2 = 1 м. Определить диаметр отверстия, если диаметр бака D = 0,5 м.
Задача 7.10
Определить первоначальный уровень в резервуаре h1, если время частичного опорожнения открытого резервуара через донное отверстия до уровня h2 = 0,7 м равно t = 70 с. Диаметр отверстия d = 0,05 м. Размеры поперечного сечения резервуара постоянные a х b = 0,8 х 0,7.
Задача 7.11
Открытый резервуар опоражнивается через коноидальный насадок диаметром d = 5 см. Определить площадь поперечного сечения резервуара, если напор воды за время t = 2 мин понизился на ΔH = 5 см и стал равным H = 35 см. Насадок присоединен к боковой поверхности резервуара.
Задача 7.12
Открытый резервуар с вертикальными стенками опоражнивается через внешний цилиндрический насадок диаметром d = 2,5 см. Через 35 с напор составил H = 1,5 см. Определить расход в начальный момент времени, если площадь поперечного сечения резервуара Ω = 1,75 м2. Насадок присоединен к отверстию на боковой стенке резервуара.
Задача 7.13
Определить время наполнения мерного бака объемом V = 0,02 м3, если истечение происходит при постоянном уровне воды, через внешний цилиндрический насадок диаметром d = 0,02 м при избыточном давлении на поверхности воды p0изб = 30 кПа. Глубина погружения насадка h = 2,4 м.
Задача 7.14
Определить расход воды через отверстие диаметром d = 0,08 м, коэффициент расхода которого μ = 0,65, если показание манометра pизб = 150 кПа, а высота установки манометра над осью отверстия h = 1,5 м.
Задача 7.15
Газ, заполняющий вертикальную трубу, вытекает в атмосферу через два насадки диаметром d = 10 мм, расположенные по высоте трубы на расстоянии a = 100 м друг от друга. Коэффициент расхода насадков (с учетом сопротивления подводящих горизонтальных трубок) μ = 0,95. Определить массовый расход M газа через каждый
насадок, если показание спиртового манометра, присоединенного к трубке у нижнего насадка, h = 200 мм (плотность спирта ρсп = 800 кг/м3). Давление атмосферного воздуха на уровни нижнего насадка pат = 100 кПа, температура воздуха и газа t = 20 ℃ . Значения удельной газовой постоянной воздуха Rв = 287 Дж/(кг·К) и газа Rг = 530 Дж/(кг·К). Скоростным напором и потерями в трубе пренебречь, плотность воздуха и газа принимать постоянными по высоте a.
Задача 7.16
Два резервуара с избыточным давлением p0и1 = 105 Па и p0и2 = 0,6·105 Па соединены между собой короткой трубой диаметром d = 20 мм. Определить расход воды в трубе, если h1 = 0,5 м до h2 = 1,4 м.
Задача 7.17
Определить коэффициенты расхода, скорости, сжатия при истечении воды в атмосферу через отверстие диаметром d = 10 мм под напором H = 2 м, если расход Q = 0,294 л/с, дальность полета струи l = 3 м. Отверстие расположено на высоте h = 1,2 м от пола.
Задача 7.18
Из открытого бака вытекает вода через малое отверстие в атмосферу. Глубина воды в баке h = 3 м поддерживается постоянной. При какой высоте h1 отверстия от пола дальность падения струи l будет максимальной.
Задача 7.19
Для задачи 4.18 определить, при какой глубине бака дальность полета будет максимальной, если отверстие расположено на высоте h1 = 1,5 м от основания.
Задача 7.20
Мазут подается в топку котла с расходом Qм = 100 кг/ч. Для сжигания мазута (ρм = 850 кг/м3) требуется воздух (ρв = 850 кг/м3) в количестве V = 8,7 м3/кг. Определить необходимые диаметры каналов для подачи воздуха и мазута, если мазут подается под давлением pи = 2,5 кгс/см2, а воздух под давлением 200 мм рт.ст. Коэффициенты скорости и расхода принять φ = μ = 0,82.
Часть задач есть решенные, контакты