Р.87
С этими задачами также ищут задачи по теплотехнике
Задача 1
Определить изменение плотности жидкости (ρ = 1000 кг/м3) при изменении давления от р1 = 1 · 105 Па до р2 = 1 · 107 Па.
Купить задачу 1
Задача 2
Определить плотность жидкости, полученной смешиванием 15 л жидкости плотностью ρ1 = 720 кг/м3 и 25 л жидкости плотностью ρ2 = 1000 кг/м3.
Купить задачу 2
Задача 3
Каким должен быть объем нефтехранилища для размещения нефти массой 60 т, удельным весом γ = 8500 Н/м3?
Купить задачу 3
Задача 4
Определить динамический коэффициент вязкости жидкости и ее относительный вес, если вязкость, определенная при помощи вискозиметра Энглера, равна 18,5°Е. Удельный вес жидкости принять γ = 8,84 кН/м3.
Купить задачу 4
Задача 5
Стальной трубопровод, заполненный водой при t1 = 10 °С, находится под давлением p = 2 · 106 Па. Диаметр трубопровода d = 0,4 м, длина 1 км. Определить давление воды в трубопроводе при повышении температуры до t2 = 15 °С.
Купить задачу 5
Задача 6
В цилиндрическом резервуаре высотой 6 м находится бензин (βt = 0,0008°С-1). При температуре t1= 15°С бензин не доходит до края на 10 см. Определить, при какой температуре бензин начнет переливаться через край резервуара.
Купить задачу 6
Задача 7
При гидравлическом испытании участка трубопровода диаметром 400 мм и длиной 600 м давление воды в трубе было повышено до 2,943 МПа. Через час оно снизилось до 1,962 МПа. Сколько воды вытекло через неплотности, если коэффициент объемного сжатия воды βр = 5 · 10-10 Па-1?
Купить задачу 7
Задача 8
При заполнении объемного гидропривода рабочая жидкость (масло) имеет температуру t1 = 15 °C. Определить температуру t2, которую может приобрести масло в процессе работы, чтобы давление в системе гидропривода повысилось не более чем на Δp = 40 МПа. Вместимость системы (объем масла до его нагревания) Wн = 20 л, βt = 0,0009 °C-1, E = 1390 МПа. (Считать, что гидропривод заполнен маслом полностью, расширительные резервуары отсутствуют, деформацию элементов гидропривода не учитывать).
Купить задачу 8
Задача 9
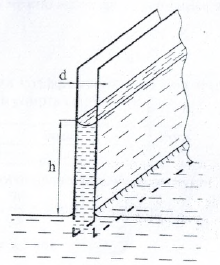
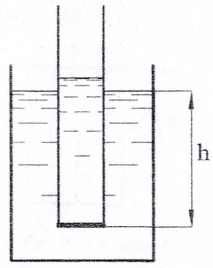
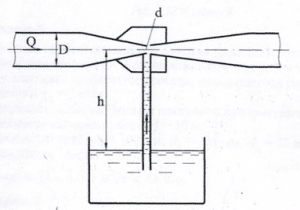
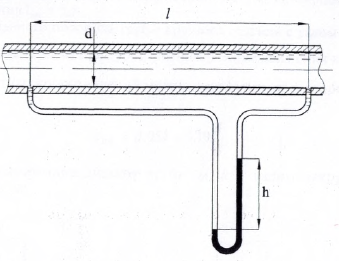
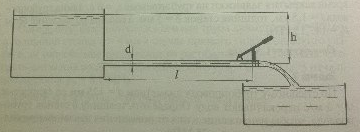
Две плоские стеклянные пластины опущены нижними концами в воду параллельно друг другу (рис. 10), расстояние между ними d = 0,2 мм. Определить дополнительное давление, возникающее в воде от действия сил поверхностного натяжения рпов, а также высоту h, на которую поднимется жидкость между пластинами. Коэффициент поверхностного натяжения воды принять равным 7,2 · 10-2 Н/м.
Купить задачу 9
Задача 10
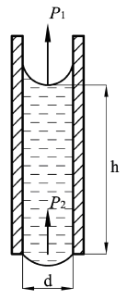
Капиллярная трубка (рис. 11) с внутренним диаметром 1 мм наполнена водой. Часть воды повисла внизу в виде капли, которую можно принять за часть сферы радиусом 5 мм. Определить дополнительные давления рдоп1 и рдоп2, возникающие от действия сил поверхностного натяжения, искривляющие верхние и нижние мениски. Чему будут равны эти давления, если вместо воды в капилляре будет находиться: спирт; бензин? Температуру жидкостей принять равной 20°С.
Купить задачу 10
1. ГИДРОСТАТИКА
1.1. Гидростатическое давление. Методы и средства для измерения давления
Задача 1
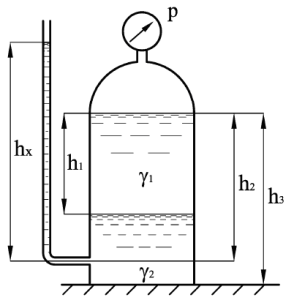
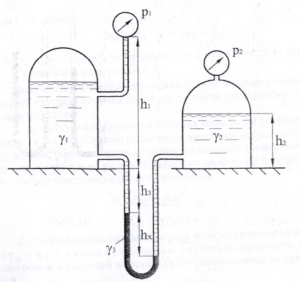
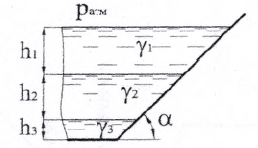
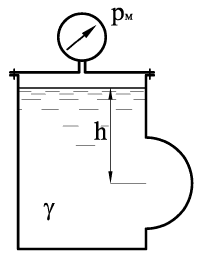
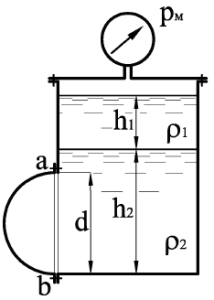
В герметически закрытом сосуде (рис. 1.15) налиты две несмешивающиеся жидкости до уровня h3 = 7 м. Показание манометра, установленного в верхней части сосуда, p = 16 кПа. Удельный вес жидкости, образующей верхний слой γ1 = 8 кН/м3, толщина этого слоя h1 = 3 м. Удельный вес жидкости нижнего слоя γ2 = 10 кН/м3. На глубине h2 = 5 м от свободной поверхности жидкости в сосуде присоединен открытый пьезометр. Определить высоту hх, на которую поднимется жидкость в пьезометре. Чему будет равно избыточное давление на дне сосуда?
Купить задачу 1
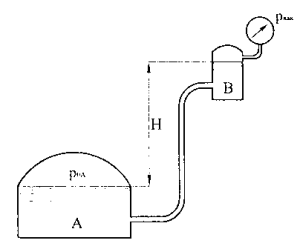
Задача 2
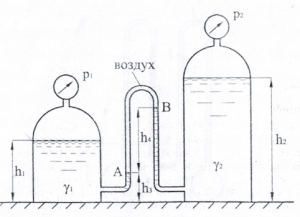
Два герметичных сосуда (рис. 1.16) наполнены жидкостями с удельными весами γ1 = 10 кН/м3 и γ2 = 12 кН/м3 на высоту h1 = 1 м и h2 = 2 м соответственно. Сосуды соединены изогнутой трубкой, частично заполненной жидкостями из сосудов. Между точками А и В находится воздух. Уровень свободной поверхности жидкости γ1 в ле вой ветви трубки относительно основания сосудов h3 = 0,4 м. Вертикаль ное расстояние между точками А и В h4 = 1 м. В верхних точках сосудов установлены манометры. Показание первого манометра р1 =5 кПа. Чему равно показание второго манометра р2, а также избыточное давление воздуха в точках А и В?
Купить задачу 2
Задача 3
Две запаянные с одного конца трубки и заполненные жидкостями с удельными весами γ1 = 11 кН/м3 и γ2 = 10 кН/м3, опрокинуты в открытые сосуды с теми же жидкостями (рис. 1.17). В запаянных трубках жидкость поднялась на высоту h1 и h2, соответственно. Принимая давление паров рассматриваемых жидкостей равным нулю, определить величину атмосферного давления, если разность высот столбов этих жидкостей составляет 0,9 м. Как изменится разность уровней жидкостей в трубках, если атмосферное давление повысится на 2%?
Купить задачу 3
Задача 4
Герметически закрытый сосуд (рис. 1.18) наполнен жидкостью с удельным весом γ1 до высоты h1 = 2 м. Избыточное давление в верхней части сосуда, измеренное манометром, p = 100 кПа. От сосуда отходит изогнутая трубка, заполненная жидкостью с удельным весом γ1, ртутью (ρрт = 13600 кг/м3) и жидкостью с удельным весом γ2 = 12 кН/м3. Высота уровней жидкостей в трубке h2 = 0,8 м, h3 = 1,5 м, h4 = 3,5 м. Определить удельный вес жидкости γ1.
Купить задачу 4
Задача 5
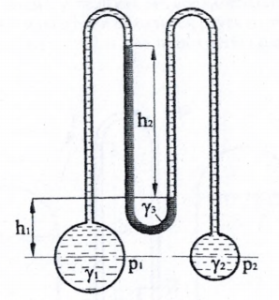
Две трубы, заполненные жидкостями γ1 = 10 кН/м3 и γ2 = 15 кН/м3, соединены изогнутой трубкой, частично заполненной ртутью γ3 = 133,4 кН/м3 (рис. 1.19). Определить разность давлений Δр = р2 – р= в центрах этих труб, расположенных в одной горизонтальной плоскости, если уровень ртути в правой ветви находится на высоте h1 = 0,5 м, а разность уровней ртути h2 = 2 м.
Купить задачу 5
Задача 6
Герметично закрытый сосуд на высоту h1 = 1,5 м заполнен жидкостью, имеющей удельный вес γ1 = 10 кН/м3 (стр. 1.20). От дна сосуда отходит изогнутая трубка, заполненная в нижней части ртутью (γ2 = 133,4 кН/м3). Уровень ртути в правой ветви трубки находится ниже дна сосуда на h2 = 1,2 м. Разность уровней ртути h3 = 0,8 м. Над ртутью в левой ветви находится жидкость, плотность которой ρ3 = 2000 кг/м3. Показание манометра, установленного на крышке сосуда р = 127,72 кПа. Определить высоту столба жидкости h4 над ртутью в левой ветви.
Купить задачу 6
Задача 7
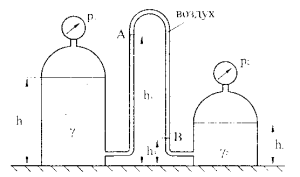
Два герметичных сосуда (рис. 1.21), основания которых расположены на одной горизонтальной плоскости, наполнены жидкостями, имеющими разные удельные веса γ1 = 20 кН/м3 и γ2 = 10 кН/м3, на высоту h1 = 2 м и h2 = 1 м. Сосуды соединены изогнутой трубкой, в которой между точками А и В находится воздушный пузырь. Нижний край пузыря расположен на высоте h3 = 0,8 м над основанием сосуда. Определить положение верхнего края пузыря hх, если показания манометров на крышках сосудов р1 = 100 кПа, р2 = 78 кПа. Чему равно избыточное давление в точках А и В?
Купить задачу 7
Задача 8
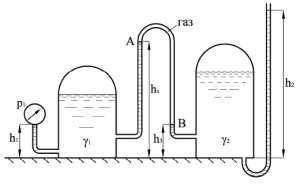
Два резервуара установлены на одной горизонтальной плоскости (рис. 1.22), соединены изогнутой трубкой, в которой между точками А и В находится газовый пузырь. Показание манометра левого резервуара, установленного на высоте h1 = 1 м над плоскостью оснований резервуаров, р1 = 100 кПа, уровень жидкости в пьезометре правого резервуара h2 = 4,75 м. Жидкость в левом резервуаре имеет удельный вес γ1 = 10 кН/м3, в правом — γ2 =20 кН/м3. Определить положение верхнего края пузыря hх, если его нижний край находится на высоте h3 = 1 м от оснований резервуаров.
Купить задачу 8
Задача 9
Два сосуда (рис. 1.23), основания которых расположены в одной горизонтальной плоскости, наполнены разными жидкостями с удельными весами γ1 = 10 кН/м3, γ2 = 20 кН/м3, соединены изогнутой трубкой, в которой между жидкостями находится ртуть (γ3 = 133,4 кН/м3). В левом сосуде на высоте h1 = 3 м над плоскостью основания установлен манометр, показывающий давление р1 = 100 кПа. На крышке правого сосуда установлен манометр, его показание р2 = 192,72 кПа. Уровень жидкости в правом сосуде h2 = 1 м над плоскостью оснований. Определить разность уровней ртути hх, если ее верхний уровень находится на h3 = 0,8 м ниже плоскости оснований сосудов.
Купить задачу 9
Задача 10
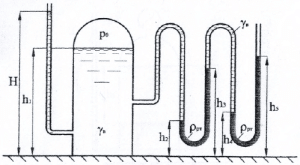
Герметично закрытый резервуар (рис. 1.24) заполнен водой до уровня h1 = 2,6 м относительно основания резервуара. Слева к резервуару присоединен пьезометр, уровень воды в котором относительно основания резервуара H. Справа к резервуару присоединена изогнутая трубка, заполненная водой и ртутью, уровни которых расположены на высоте h2 = 0,6 м, h3 = 1,6 м, h4 = 0,8 м, h5 = 1,8 м от основания сосуда. Плотность ртути ρ = 13 600 кг/м3.
Определить избыточное давление р0 воздуха в напорном баке. Какой высоты H должен быть пьезометр для измерения того же давления р0? Как изменится высота H, если р0 увеличится на 10%?
Купить задачу 10
1.1.1
Задача 1
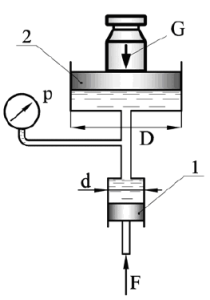
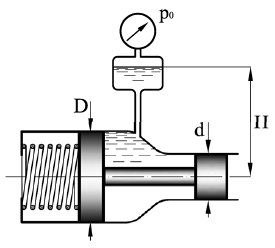
Пренебрегая разностью высот гидросистемы (рис. 1.33), определить показание манометра p и вес груза G, лежащего на поршне 2, если для его подъема к поршню 1 приложена сила F = 1,8 кН. Диаметры поршней: D = 255 мм, d = 68 мм. Разностью высот пренебречь.
Купить задачу 1
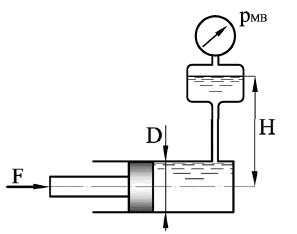
Задача 2
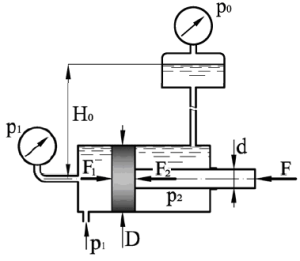
Определить избыточное давление жидкости р1 фиксируемое манометром, которое необходимо подвести к гидроцилиндру (рис. 1.34), чтобы преодолеть усилие, направленное вдоль штока F = 0,85 кН. Диаметры: цилиндра – D = 41 мм, штока – d = 16 мм. Давление в бачке р0 = 41 кПа, высота Н0 = 4,55 м. Силу трения не учитывать. Плотность жидкости ρ = 1000 кг/м3.
Купить задачу 2
Задача 3
Определить давление р в верхнем цилиндре гидропреобразователя (мультипликатора) (рис. 1.35), если показание манометра, присоединенного к нижнему цилиндру, рм = 0,35 МПа. Поршни перемешаются вверх, причем сила трения составляет 10 % силы давления жидкости на нижний поршень. Вес поршней G = 3,7 кН. Диаметры поршней: D = 370 мм, d = 75 мм; высота Н = 2 м; плотность масла ρ = 900 кг/м3.
Купить задачу 3
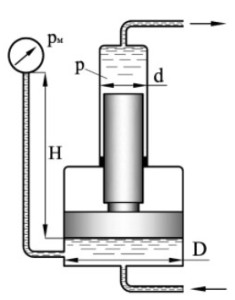
Задача 4
Определить показание мановакуумметра pмв, если к штоку поршня (рис. 1.36) приложена сила F = 0,95 кН, его диаметр D = 85 мм, высота Н = 0,98 м, плотность жидкости ρ = 800 кг/м3.
Купить задачу 4
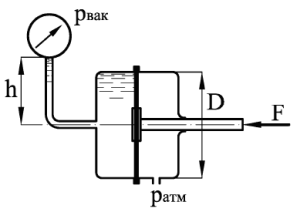
Задача 5
Определить силу F, действующую на шток гибкой диафрагмы (рис 1.37), если ее диаметр D = 225 мм, показание вакуумметра pвак = 10 кПа, высота h = 1,2 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если hатм = 760 мм рт. ст.
Купить задачу 5
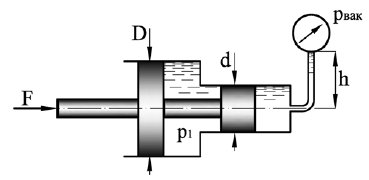
Задача 6
Определить силу F на штоке золотника (рис. 1.38), если показание вакуумметра pвак = 43 кПа, избыточное давление p1 = 0,68 МПа, высота h = 2,65 м, диаметры поршней D = 60 мм и d = 17 мм, ρ = 990 кг/м3.
Купить задачу 6
Задача 7
Система из двух поршней, соединенных штоком, находится в равновесии (рис. 1.39). Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке, – масло с плотностью ρ = 850 кг/м3. Диаметры: D = 63 мм; d = 20 мм; высота H = 950 мм; избыточное давление p0 = 8,1 кПа.
Купить задачу 7
Задача 8
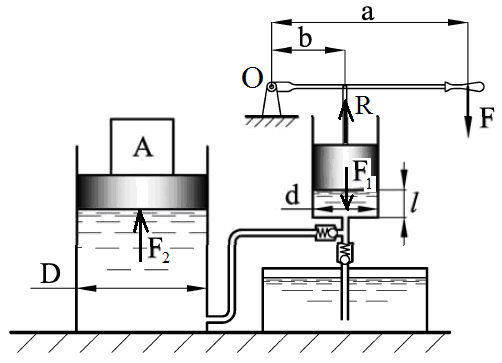
При подъеме груза (рис. 1.40) массой 6 т на высоту 0,45 м воспользовались гидравлическим домкратом с кпд 75%. Отношение площадей большого поршня к малому ω1/ω2 = D2/d2 = 100, ход малого поршня 0,2 м. Сколько ходов сделает малый поршень для подъема груза? Какое максимальное усилие F необходимо приложить к рукоятке при ходе нагнетания, если a/b = 10? Весами обоих поршней пренебречь.
Купить задачу 8
Задача 9
Какое усилие F необходимо приложить к рукоятке гидравлического домкрата (рис. 1.41), если усилие, преодолеваемое домкратом, составляет T = 29,43 кН? Сопротивления в уплотнениях поршней, в клапанах, каналах и шарнирах можно не учитывать. Диаметр большого поршня D = 45 мм, диаметр малого поршня d = 10 мм, длина плеч рычага b = 25 мм, a = 200 мм.
Купить задачу 9
Задача 10
С какой силой каждая из тормозных колодок 1 (рис. 1.42) будет прижиматься к тормозному барабану 2 колеса, если сила нажатия на малый поршень F = 850 Н? Диаметр малого поршня d = 310 мм, больших поршней D = 390 мм.
Купить задачу 10
1.2. Сообщающиеся сосуды. Закон Паскаля
Задача 1
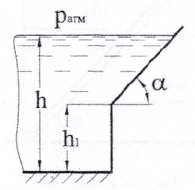
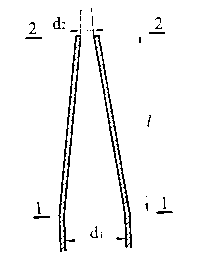
Стеклянная трубка (рис. 1.58) с одной стороны закрыта пластиной и опущена этим концом вертикально в воду на глубину 0,68 м. Какой высоты нужно налить в трубку ртуть или керосин, чтобы пластика отпала?
Купить задачу 1
Задача 2
В вертикальной перегородке закрытого резервуара (рис. 1.59) прямоугольная крышка шириной b = 0,4 м и высотой h = 0,5 м перекрывает отверстие. Правый отсек заполнен нефтью (ρ = 870 кг/м3) под избыточным давлением 12 кПа, левый — воздухом. Показание ртутною мановакуумметра, подключенного к левому отсеку резервуара, hрт = 60 мм. Определить значение и точку приложения силы давления нефти на крышку, если ее центр тяжести расположен на глубине Н = 0,75 м от свободной поверхности нефти. Атмосферное давление принять 100 кПа.
Купить задачу 2
Задача 3
Открытый резервуар заполнен тремя несмешивающимися жидкостями (рис. 1.60), имеющими удельный вес и высоту слоя соответственно γ1 = 7,8 кН/м3, h1 = 1 м; γ2 = 9,81 кН/м3, h2 = 0,7 м; γ3 = 133,4 кН/м3, h3 = 0,3 м. Определить силу избыточного давления на наклонную (α = 60°) боковую стенку резервуара, если ее ширина b = 2 м. Расчет выполнить графоаналитическим методом, построив эпюры давления.
Купить задачу 3
Задача 4
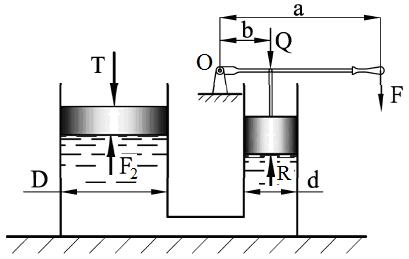
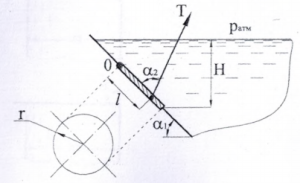
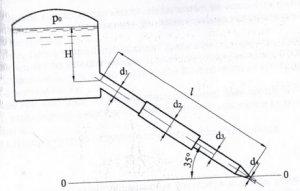
Определить натяжение каната Т, удерживающего затвор (рис. 1.61), который закрывает круглое отверстие r = 1 м в плоской наклонной стенке, если заданы следующие линейные размеры: H = 3м; l = 1,8ми углы α1 = α2 = 60º.
Купить задачу 4
Задача 5
Определить результирующую силу избыточного давления воды, действующую на плоскую ломаную стенку (рис. 1.62) шириной b = 2 м; глубина воды h = 2 м, высота нижней части стенки h1 = 1 м, угол наклона верхней части стенки к горизонтальной плоскости α = 45°. Давление на свободную поверхность жидкости – атмосферное. Построить эпюру избыточного давления воды на стенку и найти координату центра давления стенки.
Купить задачу 5
Задача 6
Четыре стенки, наклоненные к горизонтальной плоскости под углом 90°, 60°, 45° и 30° соответственно, показаны на рис. 1.63. Ширина каждой из стенок b = 1 м. Определить силу гидростатического давления воды на каждую из стенок, если уровень воды h = 1 м; на свободную поверхность воды действует атмосферное давление. На каком вертикальном расстоянии от свободной поверхности находится центр давления?
Купить задачу 6
Задача 7
Промежуточная вертикальная стенка делит емкость (рис. 1.64) шириной b = 1,2 м на два отсека. Определить значение равнодействующей сил избыточного гидростатического давления на эту стенку и точку ее приложения, а также точки приложения сил P1 и P2, если уровень воды в левом отсеке h1 = 1200 мм, а в правом – h2 = 480 мм.
Купить задачу 7
Задача 8
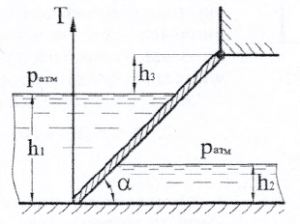
Щит, перекрывающий ирригационный канал, расположен под углом α = 45° к горизонту и прикреплен шарнирно к опоре над водой (рис. 1.65). Пренебрегая весом щита и трением в шарнире, определить усилие, которое необходимо приложить к тросу для открывания щита, если его ширина b = 1,5 м, глубина воды перед щитом h1 = 3 м, за щитом h2 = 2 м. Шарнир расположен на расстоянии h3 = 1,5 м над высшим уровнем воды.
Купить задачу 8
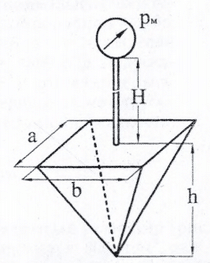
Задача 9
Емкость, наполненная жидкостью с плотностью ρ = 750 кг/м3, имеет форму перевернутой вершиной вниз пирамиды (рис. 1.66). Определить силы давления жидкости, действующие на каждую грань емкости, если рм = 200 кПа, Н = 5 м, h = 1,5 м и стороны основания пирамиды: а = 1,1 м; b = 0,8 м.
Купить задачу 9
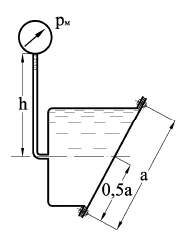
Задача 10
Определить силу давления масла (γ = 8650 Н/м3) на болты крышки (рис. 1.67), которая имеет форму прямоугольника высотой a = 0,64 м и шириной b = 1,5 м. Показание манометра рм = 120 кПа, высота h = 2 м.
Купить задачу 10
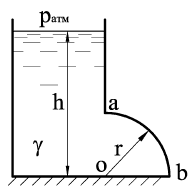
Задача 11
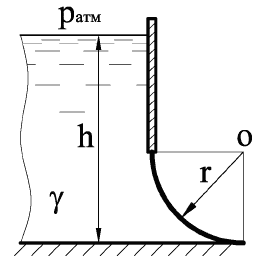
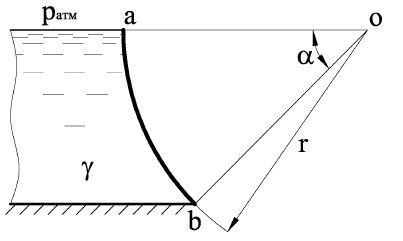
В нижней части вертикальной плоской стенки открытого резервуара имеется проем прямоугольной формы шириной b = 4 м, закрытый криволинейной крышкой ab в виде четверти боковой поверхности цилиндра радиусом r = 1 м (рис. 1.68). Глубина воды в резервуаре h = 3 м.
Определить значение и направление действия силы P давления воды на крышку.
Купить задачу 11
Задача 12
Металлическая цистерна диаметром d = 1,8 м и длиной l = 10 м полностью заполнена минеральным маслом γ = 9000 Н/м3 (рис. 1.69). Давление на поверхности масла – атмосферное. Чему равна сила избыточного давления масла на внутреннюю поверхность цистерны abc?
Купить задачу 12
Задача 13
Определить значение и направление действия силы гидростатического давления бензина (γ = 7,6 кН/м3) на полуцилиндрическую крышку радиусом r = 1 м, закрывающую прямоугольное отверстие в вертикальной стенке герметично закрытого резервуара (рис. 1.70). Показание манометра, подключенного над свободной поверхностью бензина, рм = 15 кПа. Центр отверстия расположен на глубине h = 2 м от свободной поверхности.
Купить задачу 13
Задача 14
Секторный затвор (рис. 1.71) радиусом r = 1,2 м закрывает донное отверстие прямоугольной формы в плотине. Определить значение и направление действия силы избыточного давления воды на затвор, если напор на плотине h = 5 м, ширина отверстия b = 2,5 м.
Купить задачу 14
Задача 15
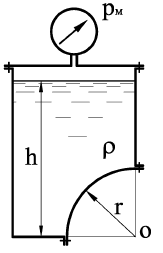
С какой силой жидкость (ρ = 800 кг/м3) воздействует на цилиндрическую крышку (рис. 1.72) радиусом r = 0,5 м и длиной l = 2 м, если избыточное давление на свободной поверхности pизб = 15 кПа?
Закрытый резервуар наполнен жидкостью на глубину h = 2,5 м?
Купить задачу 15
Задача 16
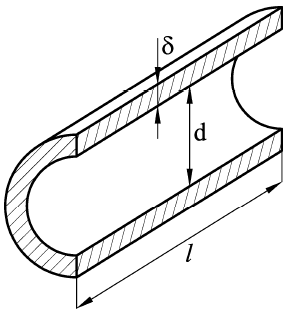
Определить минимальную толщину δ стенок водопроводной трубы (рис. 1.73) диаметром d = 50 мм, если давление воды р = 4800 кПа. Допускаемое напряжение на растяжение, возникающее в материале стенок трубопровода только от давления жидкости, σ =120 МПа.
Купить задачу 16
Задача 17
Герметично закрытый резервуар (рис. 1.74) наполнен двумя несмешивающимися (ρ1 = 800 кг/м3, ρ2 = 1000 кг/м3) жидкостями на глубину h1 = 0,5 м и h2 = 1,6 м. На свободной поверхности жидкости избыточное давление равно 12 кПа. Определить значение и направление действия силы избыточного давления на полуцилиндрическую крышку диаметром d = 0,8 м, длиной l = 2,5 м, в вертикальной стенке резервуара.
Купить задачу 17
Задача 18
Определить значение и направление силы избыточного давления воды на обшивку ab (рис. 1.75) секторного затвора радиусом r = 2 м и шириной b = 5 м. Ось вращения затвора совпадает с уровнем свободной поверхности, угол α = 45°.
Купить задачу 18
Задача 19
Герметически закрытый резервуар наполнен жидкостью, имеющий плотность ρ = 870 кг/м3.
Определить отрывающее усилие, воспринимаемое креплением полусферической крышки радиусом r = 0,8 м, если на глубине h = 1,5 м показание манометра рман = 25 кПа (рис. 1.76).
Купить задачу 19
Задача 20
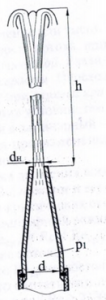
Во всасывающей трубе насоса установлен шаровой клапан диаметром D = 180 мм в седле d = 120 мм (рис. 1.77). Каким должно быть вакуумметрическое давление в центре патрубка насоса, чтобы клапан приподнялся? Превышение центра патрубка над плоскостью седла h1 = 7,5 м, клапан расположен на глубине h2 = 3 м от поверхности воды и выполнен из стали γ = 76,5 кН/м3.
Купить задачу 20
1.4. Закон Архимеда. Основы теории плавания тел.
2. ГИДРОДИНАМИКА
2.1. Уравнение Бернулли
Задача 1
На какую высоту поднимется струя воды, вытекающая из трубопровода вертикально вверх (рис. 2.8), если скорость воды в выходном сечении равна 18 м/с? Сопротивлением струи о воздух пренебречь.
Задача 2
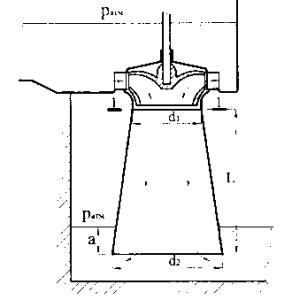
Насос подает воду в подводящую трубу эжектора под давлением р = 145 кПа. Диаметр подводящей трубы D = 120 мм, диаметр сопла d = 30 мм, атмосферное давление в месте установки эжектора ратм = 97,1 кПа. При какой подаче насоса эжектор начнет действовать, поднимая воду из резервуара, расположенного на z = 2 м ниже его оси (рис. 2.9)? Потери напора не учитывать.
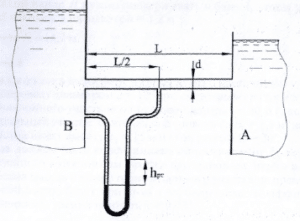
Задача 3
По трубопроводу, соединяющему два цилиндрических резервуара А и В, подается вода (ρ = 1000 кг/м3) на высоту Н = 15 м (рис. 2.10). Показание вакуумметра, установленного в резервуаре В, рвак = 45 кПа. Какое избыточное давление необходимо создать в резервуаре А для подачи Q = 540 л/с, если общие потери напора составляют 12 м, диаметры резервуаров: dА = 5 dв = 0,3 м?
Купить задачу 3
Задача 4
Чему равен перепад давления на наклонном участке трубопровода переменного сечения при перекачке по нему нефти плотностью ρ = 850 кг/м3? Скорость движения нефти в начале трубопровода υ1 = 1,2 м/с, в конце — υ2 = 6 м/с, разность отметок трубопровода z2 — 1= 4 м, потери напора на преодоление гидравлических сопротивлений составляют 1,4 м.
Купить задачу 4
Задача 5
На какой высоте от уровня воды в источнике (рис. 2.11) должен быть установлен центробежный насос, чтобы вакуум во всасывающем патрубке насоса не превышал 5,6 м? Подача насоса Q = 7 л/с, диаметр всасывающего трубопровода и патрубка d = 120 мм, общие потери напора во всасывающей линии составляют 0,5 м.
Задача 6
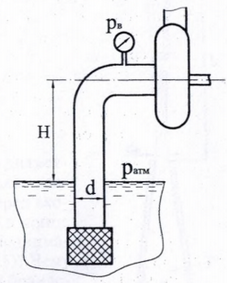
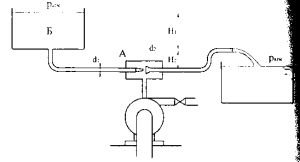
Всасывающий трубопровод и корпус центробежного насоса заполняются водой при помощи эжектора А (рис. 2.12), создающего разрежение р = 3,0 кПа.
Определить, высоту Н1 расположения напорного резервуара Б, если Н2 = 2 м, диаметр трубы d1 = 100 мм, диаметр сопла эжектора d2 = 75 мм. Найти расход воды через эжектор, пренебрегая гидравлическим потерями.
Задача 7
Вода по трубе переменного сечения (рис. 2.13), оканчивающейся коническим патрубком и расположенной под углом α = 35° к горизонту, вытекает из закрытого сосуда, находящегося под избыточным давлением р0 = 3 кПа.
Определить расход воды и построить пьезометрическую линию, пренебрегая потерями, если Н = 10 м.
Диаметры труб: d1 = 100 мм; d2 = 125 мм; d3 = 75 мм; d4 = 50 мм. Общая длина трубы l = 20 м.
Задача 8
Какое давление необходимо создать при входе в коническую трубу, установленную вертикально узким сечением вверх (рис. 2.14), чтобы скорость в выходном сечении υ2 = 14 м/с? Диаметр широкой части d1 = 500 мм, узкой — d2 = 100 мм, длина тубы l = 5 м, потери напора на рассматриваемом участке hтр = 0,6 м, коэффициент Кориолиса α = 1. Истечение происходит в атмосферу, движение плавно изменяющееся.
Задача 9
Расход воды в пожарном рукаве диаметром d = 75 мм составляет 10 л/с. Какое давление воды необходимо создать перед входом в брандспойт, установленный в конце рукава, чтобы струя воды из него поднималась не менее чем на 30 м (рис. 2.15). Чему равен диаметр выходного сечения брандспойта? Потери напора в брандспойте 0,5 м, сопротивлением воздуха пренебречь.
Задача 10
Через отсасывающую трубу гидравлической турбины (рис. 2.16) 7,1 м3/с воды отводится в реку. Труба коническая, прямоосная с диаметром в начале d1 = 1,3 м и в конце d2 = 2,1 м, длина трубы l = 2,75 м, заглубление ее под воду на а = 0,5 м. Определить давление в начале трубы.
2.2. Режимы движения жидкости
Задача 1
Определить режим движения нефти, которую подают по трубе диаметром d = 200 мм с расходом Q = 30 л/с. Вязкость нефти, выраженная в условных градусах Энглера, равна 14°.
Купить задачу 1
Задача 2
Глицерин, скипидар и этиловый спирт перекачиваются по трубопроводам одинакового диаметра d = 125 мм в количестве Q = 12 л/с. Определить режим движения каждой жидкости, а также их критические скорости. Кинематическая вязкость глицерина 1,059 Ст, скипидара – 0,0183 Ст, этилового спирта – 0,0154 Ст.
Купить задачу 2
Задача 3
По трубе диаметром d = 75 мм подается вода при температуре t = 10 °C в количестве Q = 86 см3/с. Определить режим движения потока воды. Какой расход нужно пропускать по трубе, чтобы изменить режим движения?
Купить задачу 3
Задача 4
Для охлаждения воды используют трубчатый теплообменный аппарат, оборудованный 1158 охлаждающими трубками диаметром d = 12 мм. Температура воды на входе в теплообменник 65 °С, на выходе – 45 °С. Определить режимы движения охлаждаемой воды на входе и выходе из теплообменного аппарата, если ее расход 30 л/с.
Купить задачу 4
Задача 5
Индустриальное масло ИС-20 подается по трубе диаметром 20 мм в количестве Q = 51,4 л/мин. Определить режим движения масла при температуре t1 = 15 °С и t2 = 50 °С и указать температуру, отвечающую критическому значению числа Рейнольдса. Зависимость кинематической вязкости масла от температуры показана на рис. 2.19.
Купить задачу 5
Задача 6
Вода со скоростью υ1 = 17 см/с при температуре t = 16 °С подается по трубе диаметром d1 = 20 мм. Труба постепенно расширяется до диаметра d2 = 40 мм. Определить расход воды и режимы движения в узкой и широкой частях трубы.
Купить задачу 6
Задача 7
В трубопроводе диаметром D = 100 мм с расходом Q = 7 дм3/с протекает керосин. Определить режим движения керосина, если его динамическая вязкость при температуре 15 °C μ = 0,00158 Па · с.
Купить задачу 7
Задача 8
Определить режим движения бензина (ρ = 730 кг/м3) в жиклере карбюратора, если расход бензина Q = 2,3 см3/с, диаметр жиклера d = 1,5 мм, динамическая вязкость μ = 0,00065 Па · с.
Купить задачу 8
Задача 9
Глицерин, скипидар и этиловый спирт текут по трубам прямоугольного сечения 100 х 50 мм с расходом 12 л/с. Определить число Рейнольдса для каждой жидкости, если кинематическая вязкость глицерина 1,059 Ст, скипидара — 0,0183 Ст, этилового спирта — 0,0154 Ст.
Купить задачу 9
Задача 10
Расход воды, протекающей по трубопроводу D = 150 мм, равен 20 м3/ч, температура воды t = 5°С. Какой должен быть расход, если воду заменить молоком (ν = 4,6 · 10-6 м2/с), при сохранении того же режима движения, что и у воды (ReH2O = Rемолока)?
Купить задачу 10
2.3 Потери напора
Задача 1
Принимая закон распределения квадратичным, определить эквивалентную шероховатость Δэ молокопровода длиной 300 м, диаметром 45 мм, если расход молока 1,5 л/с, плотность 1030 кг/м3, перепад давления в начале и конце молокопровода 0,1 МПа.
Купить задачу 1
Задача 2
Нефть (γ = 8340 Н/м3) движется по трубопроводу диаметром d = 0,075 м, длиной l = 200 м со скоростью υ = 0,5 м/с.
Определить потери давления на трение при движении нефти, приняв ее кинематическую вязкость ν = 0,2 Ст.
Купить задачу 2
Задача 3
Определить длину горизонтальной прямой трубы, по которой в количестве Q = 31,4 л/с прокачивается мазут (ν = 2000 мм2/с при 20°С), если внутренний диаметр трубы d = 0,25 м, а потери напора на рассматриваемом участке hL = 2,3 м.
Купить задачу 3
Задача 4
Индустриальное масло ИС-20 (ρ = 890 кг/м3) с температурой 40°С перекачивается по трубопроводу диаметром d = 0,02 м. Определить показание ртутного дифференциального манометра, присоединенного к трубопроводу (рис. 2.22), если расстояние между точками присоединения манометра l = 3 м, а расход масла Q = 0,03 м3/мин.
Купить задачу 4
Задача 5
Определить напор Н, который необходимо поддерживать в резервуаре, чтобы расход воды, пропускаемый по наклонному трубопроводу диаметром d = 100 мм и длиной l = 60 м, составлял не менее 16 л/с. Выходное сечение трубопровода расположено на расстоянии а = 1,3 м ниже входного, эквивалентная шероховатость труб Δэ = 0,2 мм, кинематический коэффициент вязкости воды ν = 0,0131см2/с.
Местными потерями и скоростным напором в резервуаре пренебречь.
Купить задачу 5
Задача 6
По трубопроводу длиной 3,5 км и диаметром d = 250 мм перекачивается жидкость с расходом Q = 70 л/с. Определить потери напора в трубопроводе, если кинематическая вязкость жидкости ν = 1,31 сСт. Трубы стальные бывшие в эксплуатации Δэ = 0,15 мм.
Купить задачу 6
Задача 7
Вода из водонапорной башни поступает к потребителям по трубопроводу диаметром d = 50 мм. Определить длину участка трубопровода l, при которой расход воды будет Q = 2 л/с, если вертикаль ное расстояние от уровня воды в водонапорной башне до центра выходного сечения трубы 30 м, эквивалентная шероховатость трубы Δэ = 0,1 мм, температура воды 10°С. Местными потерями и скоростным напором на выходе из трубы пренебречь.
Купить задачу 7
Задача 8
Определить суточную производительность нефтепровода длиной L = 3,5 км и диаметром d = 100 мм, по которому перекачивается нефть с относительным весом δ = 0,88 и кинематической вязкостью ν = 0,3 см2/с. Разность давлений в начале и конце трубопровода составляет Δp = 148 кПа.
Купить задачу 8
Задача 9
Из резервуара А в резервуар В по трубопроводу диаметром d = 250 мм и длиной L = 0,5 км перекачивают бензин (ρ = 700 кг/м3, ν = 0,75 мм2/с) с расходом Q = 42 т/ч. Определить потери давления на трение бензина о стенки трубопровода. Шероховатость стенок равна 0,2 мм.
Купить задачу 9
Задача 10
В горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных стальных труб (Δэ = 0,15 мм), протекает вода с расходом Q = 300 л/мин, температура которой t = 10°С. Наружный диаметр внутренней трубы d = 25 мм, а внутренний диаметр наружной трубы D = 75 мм. Определить потери напора на трение на участке трубопровода, длина которого l = 400 м.
Купить задачу 10
2.3.2 Местные сопротивления
Задача 1
Определить расход воды, протекающей по трубе из бака В в бак А (рис. 2.32), если показание ртутного дифманометра, присоединенного одной ветвью к баку В и другой ветвью – к сечению на середине длины трубы, равно 734 мм. Длина трубы L = 7 м, ее диаметр d = 40 мм. Коэффициент гидравлического трения λ = 0,036.
Купить задачу 1
Задача 2
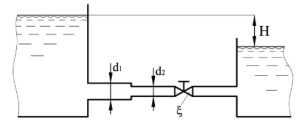
Вода перетекает из левого резервуара в правый по трубопроводу, диаметры которого d1 = 130 мм и d2 = 60 мм (рис. 2.33). Определить, пренебрегая потерями напора по длине, расход в трубопроводе, если разность уровней жидкости в резервуарах H = 9 м и коэффициенте сопротивления вентиля ξ = 5. Построить напорную и пьезометрическую линии.
Купить задачу 2
Задача 3
Определить суммарный коэффициент потерь и полную потерю напора Hw, в трубопроводе длиной l = 450 м и диаметром d = 300 мм при скорости движения воды υ = 1,5 м/с (рис. 2.34). Радиусы плавных поворотов R = 400 мм под углом 90°, углы резких переломов α = 60°, коэффициент гидравлического трения λ = 0,031.
Купить задачу 3
Задача 4
Потери напора при внезапном расширении потока в горизонтальном трубопроводе h = 0,1 м. Определить диаметр трубопровода d1 перед внезапным расширением, если расход Q = 8,9 л/с и диаметр трубы после расширения d2 = 110 мм.
Купить задачу 4
Задача 5
Вода сливается из бака А в бак В по трубопроводу, диаметр которого d = 90 мм и полная длина L = 12 м (рис. 2.35). Из бака В вода вытекает в атмосферу через цилиндрический насадок такого же диаметра d = 90 мм (коэффициент расхода μ = 0,82). Коэффициент сопротивления вентиля в трубе ξв = 6, коэффициент гидравлического трения λ = 0,03, радиус закругления угольника R = 300 мм. Определить, какой напор H нужно поддерживать в баке А, чтобы уровень в баке В находился на высоте h = 1,8 м.
Купить задачу 5
Задача 6
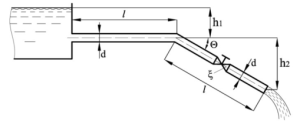
Вода вытекает в атмосферу из резервуара с постоянным уровнем по трубопроводу диаметром d = 120 мм, состоящему из горизонтального и наклонного участков одинаковой длины l = 30 м (рис. 2.3б). Горизонтальный участок заглублен под уровень на h1 = 1,5 м, наклонный участок имеет высоту h2 = 15 м и угол уклона Θ = 30°.
Каков должен быть коэффициент сопротивления ξв вентиля установленного в наклонном участке трубопровода, чтобы вакууметрическая высота в конце горизонтального участка не превышала 5 м? Какой расход будет при этом в трубопроводе? Коэффициент гидравлического трения принять λ = 0,035.
Купить задачу 6
Задача 7
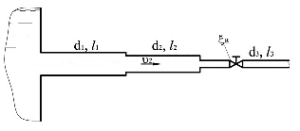
Определить потери напора hw для трубопровода с диаметрами участков d1 = 110 мм, d2 = 65 мм, d3 = 50 мм и длинами l1 = 5 м, l2 = 3 м, l3 = 1 м, если коэффициент местного сопротивления вентиля ξв = 3, скорость воды на втором участке трубопровода υ2 = 3,1 м/с. Коэффициент гидравлического трения принять λ = 0,065 (рис. 2.37).
Купить задачу 7
Задача 8
Вода, находящаяся под избыточным давлением р0 = 80 кПа, из емкости А перетекает по трубе с диаметрами d1 = 60 мм и d2 = 30 мм в приемную емкость В (рис. 2.38). Определить расход Q в трубе, если высота Н = 6 м, коэффициент сопротивления крана ξ = 8, радиусы плавных изгибов трубы 120 мм. Потерями напора по длине пренебречь.
Купить задачу 8
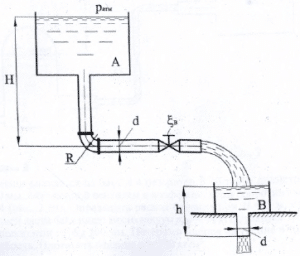
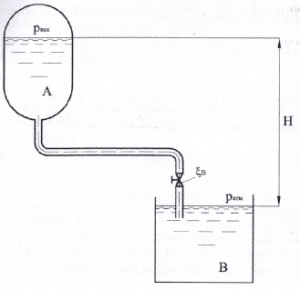
Задача 9
Бензин сливается из бака А в резервуар В по трубе диаметром d = 60 мм, снабженной вентилем с коэффициентом сопротивления ξв = 4 (рис. 2.39). Определить расход бензина при Н = 5 м, если в верхней части бака имеет место вакуум рвак = 34 кПа, радиусы плавных поворотов трубы 200 мм. Потерями напора на трение в трубе пренебречь. Плотность бензина ρ = 750 кг/м3.
Купить задачу 9
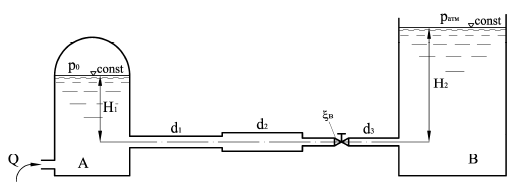
Задача 10
Вода перетекает из напорного бака А в резервуар В по трубе, состоящей из трех участков с диаметрами d1 = 50 мм, d2 = 70 мм, d3 = 40 мм (рис. 2.40). Пренебрегая потерями напора на трение по длине, определить расход, если высоты H1 = 1,5 м, Н2 = 13,5 м; избыточное давление в напорном баке р0 = 0,15 МПа, коэффициент сопротивления вентиля ξв = 5.
Купить задачу 10
2.4. Истечение жидкости через отверстия и насадки
Задача 1
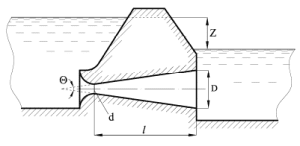
Донный водовыпуск длиной l = 4 м имеет форму конически расходящегося насадка с углом конусности Θ = 7° и работает в затопленном режиме (рис. 2.55). Определить диаметры в начале и конце водовыпуска, если расход Q = 0,54 м3/с, разность отметок уровней воды z = 0,3 м.
Купить задачу 1
Задача 2
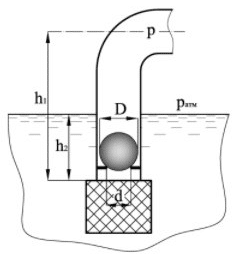
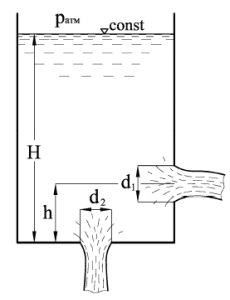
В резервуаре, наполненном бензином на высоту H = 2 м, имеются два круглых отверстия: отверстие диаметром d1 = 10 см расположено в вертикальной боковой стенке на расстоянии h = 0,5 м от дна и отверстие диаметром d2 = 8 см – в центре дна (рис. 2.56). Чему равен суммарный расход из отверстий, если отметку уровня бензина поддерживать постоянной?
Купить задачу 2
Задача 3
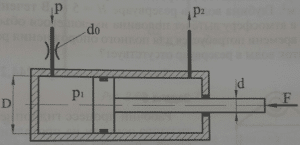
В поршневую полость гидроцилиндра подводится масло (ρ = 870 кг/м3) через дроссель диаметром d0 = 1,8 мм (рис. 2.57). Давление перед дросселем р = 13 МПа, давление на сливе р2 = 210 кПа, усилие на штоке F = 25 кН, диаметр поршня D = 100 мм, диаметр штока d = 60 мм. Определить скорость перемещения поршня, движущегося равномерно, если коэффициент расхода дросселя μ = 0,62. Трением в гидроцилиндре и утечками масла пренебречь.
Купить задачу 3
Задача 4
Истечение воды из герметически закрытого резервуара в атмосферу происходит при постоянном напоре H = 3 м через внешний цилиндрический насадок диаметром d = 10 см (рис. 2.58). Какое давление необходимо создать на свободной поверхности жидкости в резервуаре, чтобы расход при истечении не превышал Q = 60 л/с?
Купить задачу 4
Задача 5
В дне цилиндрического резервуара площадью поперечного сечения Ω = 7,5 м2 находится отверстие с острыми кромками площадью ω = 0,05 м2. Глубина воды в резервуаре Н = 5 м. В течение какого времени в атмосферу вытечет половина имеющегося объема воды? Сколько времени потребуется для полного опорожнения резервуара, если приток воды в резервуар отсутствует?
Купить задачу 5
Задача 6
Рабочий процесс гидропневмоамортизатора основан на проталкивании рабочей жидкости через отверстие и сжатии воздуха в верхней части амортизатора (рис. 2.59). Определить скорость движения цилиндра относительно поршня в начальный момент амортизации, если диаметр отверстия d = 6 мм, диаметр поршня D = 100 мм, первоначальное давление воздуха p1 = 0,3 МПа, расчетное усилие вдоль штока F = 50 кН, плотность рабочей жидкости ρ = 900 кг/м3. Коэффициент расхода отверстия μ = 0,75.
Купить задачу 6
Задача 7
Из верхнего резервуара в нижний вода поступает через донное затопленное отверстие диаметром d1 = 0,2 м, а из нижнего резервуара происходит истечение воды в атмосферу через отверстие d2 = 0,225 м (рис. 2.60). Определить напор H, необходимый для пропуска воды с расходом Q = 100 л/с при установившемся движении воды в системе резервуаров.
Купить задачу 7
Задача 8
Поршень диаметром D = 120 мм внутри гидроцилиндра демпфирующего устройства перемещается со скоростью υ = 50 см/с при нагрузке R = 20 кН. Коэффициент трения в манжете шириной δ = 12 мм равен f = 0,15. Рабочая жидкость (ρ = 850 кг/м3) перетекает из левой полости цилиндра в правую через два одинаковых отверстия в поршне. Определить диаметры отверстий, приняв коэффициент расхода отверстия μ = 0,6. Весом поршня и жидкости над ним пренебречь (рис. 2.61).
Купить задачу 8
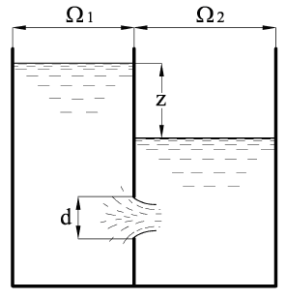
Задача 9
Определить время, в течение которого произойдет выравнивание уровней жидкости в двух смежных резервуарах с постоянными по высоте поперечными сечениями Ω1 = 2 м2 и Ω2 = 2,5 м2, если разность уровней жидкости в начале процесса истечения составляла z = 0,9 м, диаметр отверстия d = 8 см (рис. 2.62).
Купить задачу 9
Задача 10
Гидромонитор в виде коноидального насадка диаметром d = 12 мм расположен в гидрошахте на глубине h = 185 м под землей. Потери напора от насосной станции, находящейся на поверхности земли, до гидромонитора равны 5 м, если манометр на трубопроводе в насосной станции и питающий гидромонитор водой показывает давление 2,1 МПа. Определить скорость и расход струи гидромонитора.
Купить задачу 10
3.1. Гидравлический удар
Задача 1
Определить повышение давления и фазу гидравлического удара в медной водопроводной трубе после прикрытия задвижки, если расход воды снизился с 30 до 6 л/мин. Длина трубы l = 20 м, диаметр d = 35 мм, толщина стенок δ = 1 мм.
Купить задачу 1
Задача 2
Определить, разрушится ли стальная труба диаметром d = 200 мм и толщиной стенки δ = 4 мм в случае прямого гидравлического удара, если допускаемое напряжение на растяжение [σ] = 140 МПа. Скорость движения воды до гидравлического удара υ = 3 м/с, а начальное давление р0 = 0,3 МПа.
Купить задачу 2
Задача 3
Из напорного резервуара по чугунному трубопроводу длиной 300 м поступает нефть в количестве Q = 0,023 м3/с. Диаметр трубопровода d = 200 мм, толщина стенок δ = 6 мм. Определить максимальное давление в трубопроводе при закрытии задвижки, установленной в конце трубопровода, если время ее закрытия tз = 10 с, начальное давление р0 = 127,5 кПа. Произойдет ли в этом случае разрушение трубопровода ([σ] = 35 МПа)?
Купить задачу 3
Задача 4
Определить скорость распространения ударной волны и повышение давления при гидравлическом ударе в стальном трубопроводе внутренним диаметром d = 300 мм, толщина стенки δ = 7 мм и длиной 430 м, если расход воды Q = 40 л/с, а время перекрытия трубопровода 0,8 с. Какой при этом будет гидравлический удар?
Купить задачу 4
Задача 5
Вода при температуре 30 °С (ρ30 = 995,76 кг/м3, E = 2150 МПа) с расходом Q = 2,4 м3/мин подается по чугунному трубопроводу длиной l = 0,45 км, диаметром d = 200 мм и толщиной стенок δ = 5 мм. Определить наименьшее время закрытия задвижки, чтобы повышения давления в трубопроводе, вызванное гидравлическим ударом, не превышало 0,49 МПа. Какое будет напряжение σ в материале трубы при мгновенном закрытии задвижки?
Купить задачу 5
Задача 6
Напряжение материала стенок чугунного трубопровода диаметром d = 250 мм в результате гидравлического удара составило σ = 23 МПа. Определить скорость движения воды до гидравлического удара, если время закрытия задвижки на трубопроводе tз = 6 с, длина трубопровода l = 1,5 км, толщина стенок δ = 5 мм, а начальное давление воды р0 = 147,15 кПа.
Купить задачу 6
Задача 7
По стальному трубопроводу d = 125 мм со скоростью υ = 3 м/с перекачивают воду. Определить толщину δ стенок трубопровода, чтобы напряжение в них от повышения давления при гидроударе не превышало σ = 35 МПа.
Купить задачу 7
Задача 8
Определить диаметр латунного маслопровода сельскохозяйственной машины (E = 1,13 · 105 МПа), если повышение давления в случае прямого гидравлического удара не превышает Δp = 4,3 МПа. Скорость движения масла перед закрытием крана υ = 4,5 м/с, удельный вес масла γ = 9 кН/м3, модуль объемной упругости масла E0 = 1350 МПа, толщина стенок маслопровода δ = 1 мм.
Купить задачу 8
Задача 9
По бетонному трубопроводу d = 350 мм и длиной l = 560 м из напорного резервуара протекает вода в количестве Q = 0,098 м3/с. Начальное избыточное давление перед затвором, установленным в конце трубопровода, p0 = 19,62 Н/см2. Определить, какое будет давление p при внезапном закрытии затвора и через какое время t это давление распространится до напорного резервуара. Толщина стенок трубопровода δ = 40 мм.
Купить задачу 9
Задача 10
Из резервуара по стальному трубопроводу d = 75 мм под напором h = 5 м вытекает вода (рис. 2.91). Определить скорость распространения ударной волны и давление в трубопроводе при его мгновенном закрытии, если длина трубы l = 50 м, толщина стенок δ = 4 мм. Коэффициент гидравлического трения по длине λ = 0,03, местными потерями напора пренебречь.
Как изменится повышение давления в трубопроводе, если стальную трубу заменить трубой из ПВХ (E = 3000 МПа) тех же размеров?
Купить задачу 10