Р.189
Часть задач есть решенные, контакты
1. Свойства жидкости и газа
1. Вычислить коэффициент Джоуля – Томсона Δ для реального газа, подчиняющегося уравнению Ван-дер-Ваальса (p + a/v3) (v — b) = RT.
Определить также температуру инверсии Ti, при которой коэффициент Джоуля – Томсона обращается в нуль.
2. Определить, во сколько раз изменится плотность воздуха, если его нагреть от 0 до 80℃ при постоянном давлении.
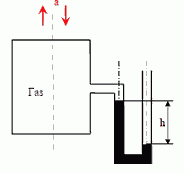
3. Масса пустого баллона вместимостью V = 50 л составляет m = 75 кг. После того, как в него накачали воздух, масса баллона с воздухом увеличилась до M = 85 кг.
Определить абсолютное давление и плотность воздуха в баллоне, если температура его t = 15℃.
4. При температуре t1 = 0℃ манометр, подключенный к баллону с воздухом, показал давление p1(м) = 20 МПа.
Как изменится показания манометра, если температура находящегося в нем воздуха повысится до t2 = 65℃.
Стоимость: 90 руб
5. Определить плотность и среднюю молекулярную массу природного газа Дашавского месторождения при нормальных условиях, имеющего следующий процентный состав по объему: CO2 – 0,05%; N2 – 1,3%; CH4 – 97,8%; C2H6 – 0,5%; C3H8 – 0,2; C4H10 – 0,1%; C5H12 – 0,05%;
6. Зависимость динамической вязкости газа μ от абсолютной температуры T выражается формулой Сезерленда μ = μ0 (T0 + C)/(T + C) (T/T0)3/2 (1), где μ — динамическая вязкость газа при абсолютной температуре T; С — постоянная для данного газа.
Найти постоянную C для воздуха, если известно, что t0 = 0℃ μ0 = 1,73 × 10-5 Па × с, а при t1 = 40℃ μ1 = 1,92 × 10-5 Па × с.
Определить также динамическую вязкость воздуха μ2 при t2 = 40℃.
7. Пользуясь формулой Сазерленда определить кинематическую вязкость метана (СН4) при температурах t1 = -10℃ и t2 = 40℃, если известно, что для метана при t1 = -10℃ μ1 = 0,00001 Па × с, постоянная C = 198 и плотность при t0 = 0℃ ρ0 = 0,716 кг/м3.
8. Определить объем, занимаемый m = 15000 кг нефти, если плотность нефти ρ = 830 кг/м3.
Стоимость: 60 руб
9. Определить плотность жидкости, если известно, что жидкость занимает объем V = 150 л, при этом масса жидкости m = 122 кг.
10. Вычислить массу нефти в цистерне, если к V1 = 7 м3 нефти с плотностью ρ1 = 820 кг/м3 добавлено V2 = 2,6 м3 нефти с плотностью ρ2 = 795 кг/м3. Определить, как и на сколько изменится плотность и объем нефти после повышения ее температуры с tн = 15℃ до tк = 35℃ (коэффициент температурного расширения нефти принять равным βt = 0,00072 1/К).
Стоимость: 150 руб
11. Вычислить кинематическую вязкость воды при t1 = 20℃, если значение динамической вязкости составляет μ = 1,02 × 10-3 Па × с (плотность воды при данной температуре принять равной ρ = 998 кг/м3). Чему будет равна кинематическая вязкость воды после повышения ее температуры на Δt = 2℃?
12. Медный шар d = 100 мм весит в воздухе Gв = 45,7 H, а при погружении в жидкость Gж = 40,6 H. Определить плотность жидкости.
13. Найти отношение удельных весов воды у поверхности Земли (γ1) и на такой высоте от поверхности, где ускорение свободного падения g2 = 4 м/с2 (γ2), если у поверхности плотность воды ρ = 1000 кг/м3.
Стоимость: 100 руб
14. Вычислить массу керосина плотностью ρ = 820 кг/м3, занимающего 90% объема десятилитровой канистры.
15. После сжатия воды в цилиндре под поршнем давление в ней увеличилось на 3 кПа. Необходимо определить конечный объем воды в цилиндре, если ее первоначальный объем составлял W1 = 2,55 л, коэффициент объемного сжатия воды βw = 4,75 × 10-10 1/Па.
16. Определить объем воды, который необходимо дополнительно подать в водовод диаметром d = 500 мм и длиной l = 1 км для повышения давления до Δp = 5 × 106 Па. Водовод подготовлен к гидравлическим испытаниям и заполнен водой при атмосферном давлении. Деформацией трубопровода можно пренебречь.
17. Определить коэффициент динамической и кинематической вязкости воды, если шарик d = 2 мм из эбонита с ρэ = 1200 кг/м3 падает в воде с постоянной скоростью u = 0,33 м/с. Плотность воды ρ = 1000 кг/м3.
2. Гидростатика
1. Определить избыточное давление в забое скважины глубиной h = 85 м, которая заполнена глинистым раствором плотностью ρ = 1250 кг/м3.
2. Определить манометрическое и абсолютное давление в точке A сосуда, заполненного водой, если h1 = 30 см, показание ртутного манометра h2 = 60 см.

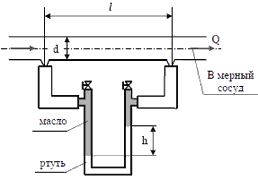
3. Определить абсолютное и избыточное давление в точке А на оси трубы, если разность уровней ртути в дифференциальном манометре hрт = 160 мм, высота масла hм = 160 мм, высота воды в резервуаре hв = 0,8 м, плотность ртути ρрт = 13,6 т/м3, плотность масла ρм = 0,85 т/м3.
Стоимость: 90 руб
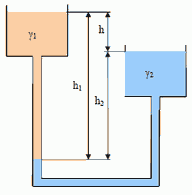
4. Два открытых сообщающихся резервуара заполнены жидкостью разного удельного веса γ1 = 8500 Н/м3 и γ2 = 10000 Н/м3. Разность уровней жидкостей в резервуарах h = 1,9 м. Определить величину h2, на которой находится граница раздела жидкостей a-a.
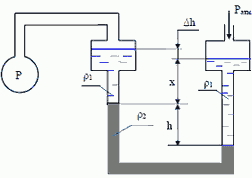
5. В герметичном сосуде — питателе А находится расплавленный баббит (ρ = 8000 кг/м3). При показании вакуумметра pвак = 0,07 МПа заполнения ковша Б прекратилось. При этом Н = 750 мм. Определить высоту уровня баббита h в сосуде – питателе А.
6. На трубопроводе диаметром d = 0,6 м, заполненном водой, установлена вертикально металлическая труба высотой h = 2,8 м, к которой подключен манометр, показание которого Рм = 3,6 ат. Определить давление на оси трубопровода.
7. Определить показания манометра, установленного на расстоянии b = 150 мм, от верхней крышки резервуара, заполненного водой, если в U – образном манометре, присоединенном к нему, высота уровня масла составляет H = 1000 мм, а превышения уровня масла над крышкой резервуара равно h = 300 мм. Плотность масла составляет ρм = 880 кг/м3.
Стоимость: 90 руб
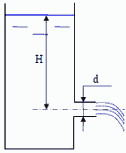
8. Определить давления газа в баллоне P по показанию h = 95 мм двухжидкосного чашечного манометра заполненного жидкостями с плотностями ρ1 = 850 кг/м3 и ρ2 = 900 кг/м3 и разница уровней в чашечках манометра Δh = 3 мм. Pатм. = 105 Па.
9. Определить разность давлений Δр в сечениях 1-1 и 2-2 газопровода, если разность уровней воды (ρв = 1000 кг/м3) в коленах дифманометра Δh = 24 см. Плотность газа ρг = 0,84 кг/м3.
Стоимость: 90 руб
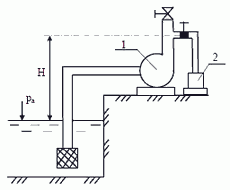
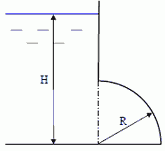
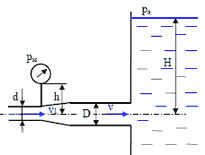
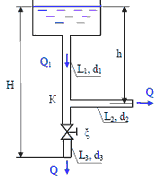
10. Для заливки центробежного насоса 1 используется вакуумный насос 2. Какой следует создать вакуум, если верх корпуса центробежного насоса находится над уровнем воды в резервуаре на расстоянии H = 7 м.
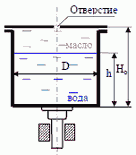
11. В цилиндрический бак диаметром D = 2 м до уровня H = 1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить вес находящегося в баке бензина, если ρб = 700 кг/м3.
12. Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра. Отметки уровней ртути от оси трубы: z1 = 1,75 м; z2 = 3 м; z3 = 1,5 м; z4 = 2,5 м.
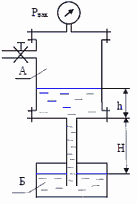
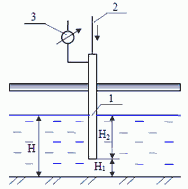
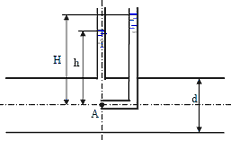
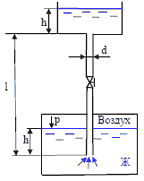
13. В канале, подводящем воду к очистным сооружениям, установлен пневматический уровнемер с самопишущим прибором.
Нижний конец трубки 1 погружен в воду на глубину H2 ниже самого низкого уровня воды в канале. В верхний конец трубки 1 по трубке 2 подается небольшой объем воздуха под давлением, достаточным для выхода воздуха в воду через нижний конец трубки 1. Определить глубину воды в канале H, если давление воздуха в трубке 1 по показаниям самопишущего прибора 3 равно h’ = 80 мм. рт. ст. и h» = 29 мм рт. ст. Расстояние от дна канала до нижнего конца трубки H1 = 0,3 м.
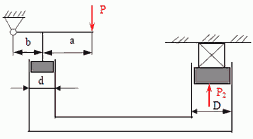
14. Гидравлический пресс имеет диаметр большого поршня D = 250 мм, меньшого d = 25 мм. Плеча рычага а = 1 м b = 0,2 м. Какое усилие надо приложить к концу рычага, чтобы сжать изделия N силой P2 = 100 кН. Трениям пренебречь.
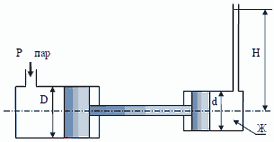
15. Паровой прямодействующий насос подает жидкость Ж (масло турбинное) на высоту Н = 45 м. Каково рабочее давление пара, если диаметр парового цилиндра D = 180 мм, а насосного цилиндра d = 100 мм? Потерями на трения пренебречь.
3. Гидродинамика
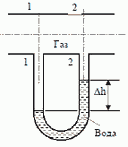
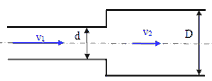
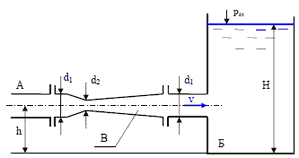
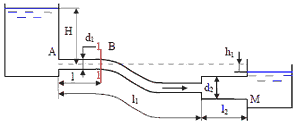
1. Жидкость вытекает из открытого резервуара в атмосферу через трубу, имеющую плавное сужение до диаметра d1, а затем постепенное расширение до d2. Истечение происходит под действием напора H = 3 м.
Пренебрегая потерями энергии, определить абсолютное давление в узком сечении трубы 1-1, если соотношение диаметров d2/d1 = √ 2; атмосферное давление соответствует hа = 750 мм рт. ст.; плотность жидкости ρ = 1000 кг/м3. Найти напор Hкр, при котором абсолютное давление в сечении 1-1 будет равно нулю.
2. При внезапном расширении трубопровода скорость жидкости в трубе меньшего диаметра равна v1 = 4 м/с. Определить разность показаний пьезометров h, если отношение диаметров труб D/d =2. Потерями напора пренебречь.
3. По трубе диаметром d = 50 мм движется вода. Определить расход, при котором турбулентный режим движения сменится ламинарным, если температура воды t = 15℃.
Стоимость: 120 руб
4. Даны два сечения трубопровода длиной l = 150 м. В начале трубопровода в сечении 1-1 диаметр d1 = 160 мм, геометрическая высота положения сечения z1 = 3м, соответственно в сечении 2-2 d2 = 130 мм и z2 = 5 м; расход жидкости Q = 0,03 м3/с, гидродинамический напор в начале трубопровода Н = 30 м, потери напора в начале трубопровода составляют h0-1 = 2 м, в конце трубопровода — h1-2 = 10 м; α = 1 – коэффициент неравномерности распределения скорости в сечении потока.
Определить:
1) Скорость движения жидкости и величину скоростного напора в каждом сечении трубопровода;
2) Величину полного гидродинамического напора в конце трубопровода;
3) Построить сечение трубопровода относительно горизонтальной плоскости, напорную линию, пьезометрическую и линию полного гидродинамического напора.
5. Определить режим движения жидкости в трубопроводе диаметром d = 500 мм при протекании в нем воды с расходом Q = 200 л/с. Температура воды 20℃.
6. Горизонтальная труба диаметром d = 100 мм внезапно расширяется до диаметра D = 200 мм. Определить потери напора, если расход равен Q = 0,05 м3/с.
7. По длинной трубе диаметром d = 50 мм протекает жидкость (ν = 2 Ст; ρ = 900 кг/м3). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (H = 80 см).
Стоимость: 120 руб
8. Определить расход воды в трубе диаметром d1 = 100 мм, имеющей плавное сужение до диаметра d2 = 50 м, если показания пьезометров: до сужения h1 = 90 см; в сужении h2 = 30 см.
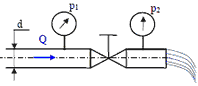
9. При закрытом положении крана, манометр, установленный на короткой трубе перед краном, показывает давление p1 = 2,5 атм, при открытом кране показание манометра равно p2 = 1,0 атм.
Пренебрегая гидравлическим сопротивлением, определить среднюю скорость v1 и расход Q воды, если диаметр трубы d = 50 мм.
Стоимость: 150 руб
10. Для определения вязкости масла измеряется потеря напора при его прокачке через калиброванную трубку диаметром d = 6 мм. Каково значение динамического коэффициента вязкости μ, если при расходе Q = 7,3 см3/с показания ртутного дифманометра, подключенного к участку трубки длиной l = 2 м, равно величине h = 12 см? Плотность масла ρм = 900 кг/м3.
11. Поток воды движется по напорному трубопроводу диаметром d1 = 40 мм с расходом Q = 0,5 л/с. Определить среднюю скорость потока при переходе на диаметр вдвое меньший.
12. Определить диаметр трубопровода, по которому подается жидкость (ν = 7,3 × 10-3 см3/с) расходом Q = 3,5 л/с, из условия получения в нем максимально возможной скорости при сохранении ламинарного режима.
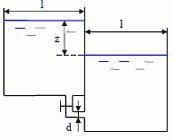
13. Определить расход воды, если разность показаний пьезометров равна h.
Дано: h = 200 мм, D = 150 мм, d = 100 мм.
4. Насадки
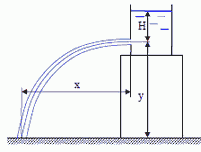
1. При истечении жидкости через отверстие диаметром do = 10 мм измерены: расстояние х = 5,5 м, высота у = 4 м, напор H = 2 м и расход жидкости Q = 0,305 л/с. Подсчитать коэффициенты сжатия ε, скорости φ, расхода m и сопротивления ξ. Распределение скоростей по сечению струи считать равномерным. Сопротивлением воздуха пренебречь.
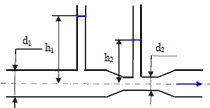
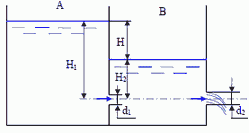
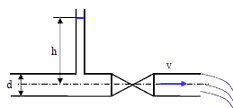
2. Из резервуара A, приток воды в который Q = 0,5 л/с через малое отверстие диаметром d1 = 15 мм, вода перетекает в резервуар B, а через отверстие диаметром d2 – в атмосферу. Определить при каком диаметре d2 напор H2 = 0,5Н1.
3. Определить напор в баке, если расход воды при истечении через цилиндрический насадок диаметром d = 0,05 м составляет Q = 0,05 м3/с. Истечение происходит при постоянном напоре.
4. В баке, имеющем в дне отверстия диаметром d1 = 100 мм и в стенке цилиндрический насадок диаметром d2 = 100 мм, установился уровень воды на высоте Н = 1,6 м. Определить, какой расход воды поступает в бак, если центр цилиндрического насадка возвышается над дном бака на высоте h = 0,2 м.
Стоимость: 90 руб
5. В бак, разделенный тонкой перегородкой на два отсека, поступает вода с расходом Q = 25 л/с. В перегородке имеется отверстия диаметром d1 = 75 мм. Из второго отсека вода сливается наружу через цилиндрический насадок диаметром d2 = 75 мм. Определить глубины воды H1 и H2 в отсеках над центром отверстия.
6. Определить какой напор необходимо создать в открытом резервуаре диаметром d = 0,09 м чтобы из отверстия диаметром d0 = 0,06 м расположенного в центре дна резервуара, вытекала струя расходом Q = 0,005 м3/с, коэффициент расхода μ = 0,62.
7. Определить объем воды V, налитой в цилиндрический бак диаметром D = 0,8 м, если вся вода вытекла из бака через отверстия в дне диаметром d = 100 мм за время t = 60 c. Какое время t1 потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?
8. Бак разделен на два отсека тонкой перегородкой. Из отсека I вода через отверстия в перегородке диаметром d1 = 3,5 см, расположенном на высоте h1 = 3,0 м от дна, поступает в отсек II, а из отсека II через внешний цилиндрический насадок диаметром d2 = 4,0 см выливается наружу. Высота расположения насадка над дном – h2 = 1,0 м. Уровень воды над центром отверстия в отсеке I ровен Н1 = 4,0 м. Движения установившееся.
Требуется определить:
1. Расход Q.
2. Перепад уровень воды в отсеках h.
Стоимость: 120 руб
9. В дне бака расположены три одинаковые квадратные отверстия со стороной, а = 3,5 см. Одно отверстие расположено в центре дна, другое – одной стороной примыкает к боковой стенке, третье расположено в углу дна. Глубина воды в баке h = 85 см.
Определить:
1) Суммарный расход Q1 из отверстий, если давление на поверхности воды атмосферное p0 = 1,0 ат.
2) Суммарный расход Q2 из отверстий, если давление на поверхности воды p0 = 1,8 ат.
10. Определить время выравнивание уровней воды в двух соседних камерах многокамерного шлюза при следующих данных: ширина камеры b = 30 м, длина камер l = 70 м, диаметр трубы, соединяющей камеры d = 1,1 м, перепад уровней воды z = 5 м. Коэффициент расхода для водопроводной галереи принять μ = 0,70.
Стоимость: 90 руб
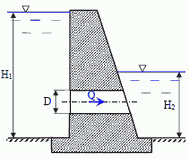
11. В теле плотины уложены две железобетонные водопропускные трубы. Глубина воды перед плотиной (в верхнем бьефе) H1 = 13 м, а за плотиной (в нижнем бьефе) H2 = 4 м. Определить диаметр труб, длина которых равна l = 6 м, если расход воды, пропускаемый двумя трубами, равен Q = 6,5 м3/с.
5. Давление жидкости
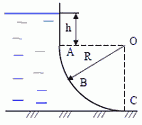
1. Построить эпюру распределения гидростатического давления воды на цилиндрическую поверхность АВС, эпюры горизонтальной и вертикальной составляющих на эту поверхность. Определить силу гидростатического давления воды P на поверхность АВС и центр давления, если радиус цилиндрической поверхности равен R = 1,2 м, длина образующей цилиндра L = 2,0 м, точка A находится на глубине h = 0,7 м.
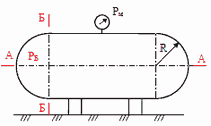
2. Горизонтальный цилиндрический резервуар, днища которого представляют собой полусферы радиусом R = 0,6 м, заполнен водой под давлением. Манометр показывает избыточное давление Pм = 0,2 атм = 19620 Па, длина L = 2,4 м.
Вычислить усилия, разрывающие резервуар по сечению А-А, и усилия, отрывающие днища резервуара (сечения Б-Б).
3. Водопровод из стальных труб повернут на угол α = 60°. Определить усилие R, на которое должен рассчитываться упор, если диаметр водопровода d = 100 мм, давление воды в нем p = 15 ат = 1471500 Па.
Стоимость: 90 руб
4. Определить силу давления воды на деталь, имеющую форму четверти круглого цилиндра радиусом R = 0,5 м. Глубина воды в сосуде H = 3 м. Расчет вести на единицу длины конструкции. Показать эпюры вертикальной и горизонтальной составляющей силы давления.
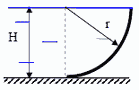
5. Определить величину и направление силы давления на цилиндрическую поверхность, удерживающую жидкость с плотностью ρ = 1000 кг/м3 и глубиной H = r = 1 м и шириной b = 2 м.
6. Определить величину и точку приложения силы гидростатического давления на плоскую боковую стенку, если глубина воды Н = 2 м, а ширина стенки B = 3 м. Построить эпюру избыточного гидростатического давления.
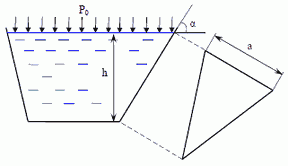
7. В резервуар прямоугольного сечения с размерами a = 1 м, b = 3 м налита жидкость — вода, плотностью ρ = 1000 кг/м3, высота жидкости h = 4,4 м.
Построить эпюру гидростатического избыточного давления на дно и одну из стенок резервуара. Определить силы давления на дно и стенку и точки приложения сил.
Стоимость: 120 руб
8. Для заданной плоской боковой стенки сосуда определить суммарную силу давления и место положения центра давления при различной плотности жидкости.
Исходные данные: a = 2 м; h = 2 м; α = 45℃ P0 = 0,3 МПа; ρ = 900 кг/м3; lт = l/3 м; I0 = al3/36.
Стоимость: 150 руб
9. Для заданной плоской боковой стенки сосуда определить суммарную силу давления и место положения центра давления при различной плотности жидкости.
Исходные данные: a = 2,5 м; h = 3 м; α = 60 ℃ P0 = 0,4 МПа; ρ = 800 кг/м3; lт = l/2 м; I0 = al3/12.
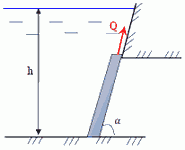
10. Плоский щит перекрывает канал шириной b = 1,8 м. Глубина воды перед щитом h = 2,5 м. Определить силу давления воды на щит и точку приложения этой силы аналитическим и графоаналитическим методом. Определить минимальное подъемное усилие щита T, если его вес G = 20 кН. Коэффициент трения щита по опорам при подъеме f = 0,25.
11. Плоский затвор испытывает воздействия жидкости. Определить:
1) величину силы давления жидкости на затвор и точку ее приложения;
2) усилия для открытия затвора.
Дано: h = 1,7 м; высота – a = 1,1 м; ширина – b = 1,5 м; вес затвора – G = 20 кН; угол наклона α = 75°; коэффициент трения скольжения – f = 0,15.
Стоимость: 150 руб
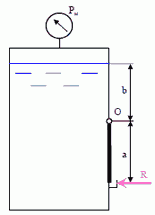
12. Определить величину усилия F, которое нужно приложить к рычагу, чтобы повернуть затвор ОВ вокруг оси O для выпуска жидкости (воды) из трубы. Задано показания вакуумметра PВ = 60 мм рт. ст. = 7999 Па, диаметр трубы D = 0,5 м и длина рычага a = 0,4 м.
13. Определить силу R, на которую должно быть рассчитано запорное устройство квадратной крышки размерами a x a (a = 0,5 м), вращающего вокруг оси O, если показания манометра Pм = 7,848 кПа, глубина погружения уровня оси b = 0,8 м, жидкость – вода. Построить эпюру давления.
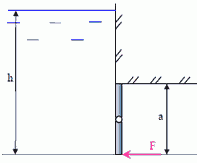
14. Затвор квадратного сечения со стороной a = 2,6 м, может вращаться вокруг горизонтальной оси O, проходящей через центр затвора. Определить силу F, которую нужно приложить к нижней кромке затвора, чтобы его закрыть, если глубина воды перед затвором h = 4,2 м. В штольне справа воздух. Трением пренебречь, ρ = 1000 кг/м3.
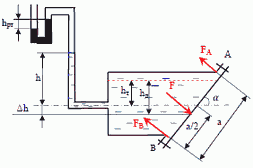
15. Определить силы, действующие на верхние FA и нижние FB болты крышки, которая имеет форму прямоугольника высотой a = 0,64 м и шириной b = 1,5 м. Показания ртутного вакуумметра hрт = 150 мм, высота h = 2,2 м. Угол наклона крышки α = 45°.
16. Для измерения ускорения горизонтально движущегося тела может быть использована закрепленная на нем U-образная трубка малого диаметра, наполненная жидкостью.
С каким ускорением движется тело, если при движении установилась разность уровней жидкости в ветвях трубки, равная h = 5 см при расстоянии между ними l = 30 см?
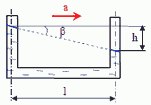
17. Призматический сосуд длинной 3l = 3 м и шириной c = 1 м, перемещающийся горизонтально с постоянным ускорением a = 0,4g, разделен на два отсека, заполненных водой до высот h1 = 1 м и h2 = 1,75 м.
Определить:
1) Суммарную силу давления воды на перегородку.
2) Ускорение, при котором эта сила станет равной нулю.
18. Найти зависимость показания h водяного манометра (радиусы ветвей R1 и R2 заданы), присоединенного к замкнутому сосуду, который наполнен газом, находящимся под вакуумом pв, от:
1) поступательного ускорения сосуда (a), направленного по вертикали вверх и вниз; 2) угловой скорости вращения сосуда (Ω).
19. Открытый в атмосферу вертикальный цилиндрический сосуд радиусом R = 0,4 м заполнен первоначально h = 1,0 м водой при температуре t = 40℃. Сосуд приводится во вращения с числом оборотов n, обеспечивающим касания дна вершиной параболоида. Определить высоту поднятия воды в сосуде и силу гидростатического давления на дно сосуда.
20. Цилиндрический сосуд диаметром D = 600 мм и высотой Ho = 500 мм заполнен водой до h = 400 мм. Остальной объем сосуда заполнен маслом (ρ = 800 кг/м3). Сосуд закрыт крышкой с малым отверстием в центре и приведен во вращение относительно центральной вертикальной оси.
Определить, с какой угловой скоростью Ω нужно вращать сосуд для того, чтобы поверхность раздела жидкостей коснулась дна сосуда. Найти усилия, действующие при этом на дно и крышку сосуда.
6. Расчет сопротивлений
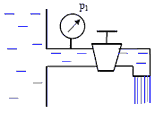
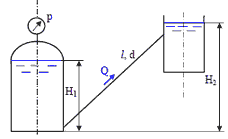
1. Для измерения расхода воды, которая подается по трубе А в бак Б, установлен расходомер Вентури В. Определить максимальный расход, который можно пропускать через данный расходомер при условии отсутствия в нем кавитации, если температура воды t = 60℃ (давления насыщенных паров соответствует hн.п. = 2 м вод. ст.). Уровень воды в баке поддерживается постоянным, равным H = 1,5 м; h = 0,5 м. Размеры расходомера d1 = 50 мм; d2 = 20 мм. Атмосферное давления принять равным pат = 760 мм рт. ст. = 101325 Па. Коэффициент сопротивления диффузора ζд = 0,2.
2. Определить среднюю скорость и расход жидкости в трубопроводе диаметром d = 5,9055 дюймы, если потери напора на участке длиной L = 300 м составляют hд = 3 м. Коэффициент гидравлического трения λ = 0,02.
3. На трубопроводе диаметром d = 300 мм перед задвижкой установлен пьезометр, показания которого h = 2 м. Расход воды Q = 100 л/с, давление за задвижкой атмосферное. Определить коэффициент сопротивления задвижки.
Стоимость: 120 руб
4. Вентиляционная труба d = 0,1 м имеет длину l = 100 м. Определить давление, которое должен развивать вентилятор, если расход воздуха, подаваемый по трубе Q = 0,078 м3/с. Давление на входе в трубу p = pатм = 101 кПа. Местных сопротивлений по пути не имеется. Температура воздуха 20 ℃. Вязкость воздуха при t = 20℃, ν = 15,7 × 10-6 м3/с, абсолютная эквивалентная шероховатость стенок воздуховода Δ = 0,2 мм. Коэффициент гидравлического трения следует определять по формуле А.Д. Альтшулля.
5. Определить сопротивление крана, регулирующего расход, если при расходе Q = 10 л/с и диаметре трубы d = 50 мм манометры, установленные до крана и после него, показывают соответственно p1 = 2 кг/см3 и р2 = 1 кг/см3.
6. Определить расход жидкости, вытекающей из трубы диаметром d = 16 мм через плавное расширение (диффузор) и далее по трубе диаметром D = 20 мм в бак. Коэффициент сопротивления диффузора ξ = 0,2 (отнесен к скорости в трубе), показания манометра pм = 20 кПа; высота h = 0,5 м; H = 5 м; плотность жидкости ρ = 1000 кг/м3. Учесть потери на внезапное расширение, потерями на трения пренебречь, режим течения считать турбулентным.
7. В середине прямолинейного участка напорной трубы диаметром d = 60 мм и длиной l = 100 м установлена задвижка с коэффициентом гидравлического сопротивления ζ3= 4. Расход жидкости в трубе Q = 10 л/с, а коэффициент гидравлического трения λ = 0,036. Найти общую (суммарную) потерю напора.
Стоимость: 60 руб
8. Вода подается по трубе диаметром d = 50 мм. В трубе установлен гидродроссель, коэффициент местных гидравлических потерь которого ζ = 15. Чему равны потери давления в этом гидродросселе, если расход воды Q = 20 л/с?
9. Вода подается по трубе диаметром d = 50 мм и длиной l = 10 м с расходом Q = 0,02 м3/с. Чему равны потери напора на трение по длине, если коэффициент потерь на трение (коэффициент Дарси) λ = 0,03?
Стоимость: 60 руб
10. Чему равна величина потерь напора на внезапное расширение при попадании жидкости с вязкостью v = 0,2 см2/с из трубы диаметром d = 20 мм под уровень в бак, если расход Q = 3,14 л/с?
7. Простые трубопроводы
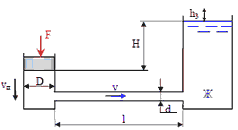
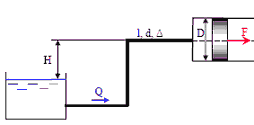
1. Поршень диаметром D = 210 мм движется равномерно вниз в цилиндре, подавая жидкость Ж (бензин) в открытый резервуар с постоянным уровнем. Диаметр трубопровода d = 70 мм, его длинна l = 21 м. Когда поршень находится ниже уровня жидкости в резервуаре на Н = 5 м, потребная для его перемещения сила равна F = 16700 Н. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии для трубопровода. Коэффициент гидравлического трения трубы принять λ = 0,03. Коэффициент сопротивления входа в трубу ξвх = 0,5. Коэффициент сопротивления выхода в резервуар ξвых = 1,0.
2. Известны коэффициенты сопротивления: гидравлического трения λ = 0,024; сужения ξс = 0,09; вентиля ξв = 6. Используя также приведенные на рисунке данные, определите:
1) расход потока воды Q;
2) давления в сечении В-В;
3) давления в сечении С-С. Учесть потери напора в двух расширениях потока.
3. Напорное сооружение (резервуар, насосная станция) обеспечивает подачу жидкости по трубопроводу потребителю. По исходным данным решить одну из задач гидравлического расчета труб определение диаметра трубы. По результатам расчета построить график напорной и пьезометрической линии.
Дано: расход – Q = 1,5 л/с; показатели манометра p = 0,07 МПа; высоты – (H1 = 1,5 м; H2 = 5 м); длина трубопровода — l = 24 м; диаметр трубопровода – d =?; материал трубопровода – сталь не знает коррозии; жидкость – вода; температура – t = 12℃.
Стоимость: 250 руб
4. Трубопровод состоит из труб двух диаметров: d = 70,7 мм и D = 100 мм. На трубопроводе установлены три пьезометра, причем высоты столбов воды h во всех пьезометрах одинаковы, но жидкость в первом пьезометре испытывает действия силы P = 0,2 Н, приложенной к поршеньку П диаметром dп = 1см. Считая коэффициент гидравлического трения λ на всем протяжении трубопровода одинаковым, определите расход воды в нем Q.
5. По трубопроводу диаметром d = 100 мм и длиной l = 3 м движется жидкость Ж (масло веретенное) (рис.). Чему равен напор H, при котором происходит смена ламинарного режима турбулентным? Местные потери напора не учитывать. Температура жидкости t = 20℃. Указания. Воспользоваться формулой для потерь на трения при ламинарном режиме (формула Пуазейля).
6. Ось горизонтального участка трубы АВ расположена на высоте h1 = 0,25 м над уровнем воды в резервуаре М, а ось участка трубы диаметром d2 лежит ниже уровня воды в резервуаре М на величину h2 = 0,5 м. Длины и диаметры участков: l1 = 30 м; d1 = 50 мм; l2 = 10 м; d2 = 100 мм. Коэффициенты потерь в закруглении ζзакр = 0,15 и коэффициенты трения λ1 = λ2 = 0,03. Определить напор Н, при котором давления p1 в сечении 1-1, отстоящем от начала трубопровода АВ на расстоянии l = 10 м, достигнет 19,6 кПа (0,2 атм).
7. Жидкость Ж (керосин) в открытый верхний бак по вертикальной трубе длинной l = 6 мм и диаметром d = 30 мм за счет давления воздуха в нижнем замкнутом резервуаре. Определить давления p воздуха, при котором расход будет равен Q = 1,5 л/с. Принять коэффициенты сопротивления: вентиля ξв = 8,0; вход в трубу ξвх = 0,5; выхода в бак ξвых = 1,0. Эквивалентная шероховатость стенок труб Δ = 0,2 мм.
Стоимость: 150 руб
8. Дано: H = 1 м; d = 0,05 м; Δ = 0,4 мм; F = 1300 Н; D = 0,15 м; l = 4 м. Жидкость – вода, плотность ρ = 1000 кг/м3 ; кинематическая вязкость ν = 1 × 10-6 м3/с. Определить расход Q.
9. Определить потери напора в трубопроводе прямоугольного сечения размером (300 х 400) мм и длиной L = 300 м. Эквивалентная шероховатость Δ = 0,3 мм, расход воды Q = 60 л/с. Температура 20℃.
Стоимость: 120 руб
10. Определить потери напора в стальном трубопроводе (Δ = 0,5 мм) диаметром d = 100 мм и длиной L = 500 м, если расход воды Q = 50 л/с, а ее температура 20℃.
11. Определить потери в трубопроводе диаметром d = 0,5 м и длиной L = 750 м при движении в нем воды с расходом Q = 0,25 м3/с. Удельное сопротивление Акв = 4,21 с3/м6.
12. Определить напор, необходимый для пропуска расхода воды Q = 0,06 м3/с через трубопровод диаметром d = 300 мм и длиной L = 1500 м. Удельное сопротивление Акв = 0,504 с3/м6.
8. Сложные трубопроводы
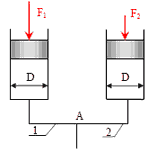
1. Перемещения поршней гидроцилиндров с диаметром D, нагруженных силами F1 = 9500 Н и F2 = 1350 Н, осуществляется подачей минерального масла по трубам 1 и 2 с одинаковым диаметрами d = 4 см. Суммарный коэффициент сопротивления первого трубопровода ζ1 = 18. Каким должен быть суммарный коэффициент сопротивления второго трубопровода, чтобы при расходе Q = 14 л/с в магистрали скорости поршней были одинаковыми?
2. По двум одинаковым, открытым в атмосферу стальным трубам (Δ = 0,2 мм) длинами L2 = L3 = 25 м и диаметрами d2 = d3 = 50 мм требуется подавать одинаковые расходы Q = 5 л/с во-ды (ν = 0,01 Ст) при напорах H = 10 м, h = 7м. Определить необходимый для этого диаметр d1 подводящей стальной трубы, длина которой L1 = 50 м, а также необходимое значение коэффициента сопротивления ξ вентиля, установленного на трубе 3. Какой расход Q’ пойдет по трубопроводу и какое избыточное давления будет в узле К, если полностью закрыть вентиль на трубе 3?
3. Насосная станция перекачивает нефть (ρ = 900 кг/м3) из пункта A в пункт B по трубопроводу, имеющему длину L = 4000 м и диаметр d = 100 мм. Причем избыточное давления в начале трубопровода равно 22 кгc/см3. Определить: 1) расход нефти в трубопроводе; 2) какую длину X должен иметь параллельно подключенный трубопровод (так называемый «лупинг») того же диаметр, чтобы давления на станции при той же подаче упало до p = 18 кгc/см3? Кинематический коэффициент вязкости нефти ν = 0,7 см3/с. Абсолютная шероховатость внутренних стенок труб равна Δ = 0,1 мм. Местные потери напора составляют 10% от потерь напора по длине.
Стоимость: 150 руб
4. Насос подает керосин в трубопровод. Размеры труб d1 = 82 мм, l1 = 53 м, d2 = d3 = 62 мм, l2 = l3 = 55 м, шероховатость Δ = 0,5 мм, коэффициент сопротивления вентиля ζ = 5, высоты расположения выходных сечений H2 = 4,6 м, H3 = 5,3 м. Расход насоса Q1 = 0,04 м3/с.
Определить:
1) расходы жидкости на участках 2 и 3;
2) давления на выходе из насоса (в сечении 1-1);
3) при каких значениях диаметров d2 и d3 расходы на участках 2 и 3 будут равны?
5. Определить общий расход воды Q1, поступающей по системе труб под напором H = 5,12 м. Диаметры труб: d1 = 150 мм; d2 = d3 = d4 = d = 125 мм. Длина труб: L1 = 160 м; L2 = L3 = L4 = L = 80 м. Воспользоваться значениями расходных характеристик для новых водопроводных (стальных) труб.
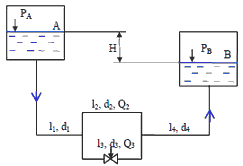
6. Определить давление в баке A — PA, если в трубопроводе будет двигаться вода с расходом Q = 0,085 м3/с. Баки A и B соединены сложным трубопроводом. Размеры труб: d1 = d4 = 120 мм, d2 = d3 = 90 мм, l1 = l4 = 105 м, l2 = l3 = 80 м. Давления в баке В — PВ = 0,1 МПа (вакуум). Коэффициенты сопротивления трения в трубах равны: λ1 = λ2 = λ3 = 0,025, λ4 = 0,02; коэффициент сопротивления задвижки равен ζ = 29. Остальными местными сопротивлениями пренебречь. Разность уровней жидкости в баках H = 30 м.
7. Трубопровод, пропускающий расход Q = 33 л/с, разветвляется в точке А на два, которые соединяются в точке В. Перепад давлений в точках А и В составляет Δр = 0,49 МПа. Определить диаметры участков трубопровода d1 и d2, исходя из того, чтобы расход на втором участке был бы в два раза больше, чем на первом. Коэффициенты местных гидравлических сопротивлений участков соответственно равны ξ1 = 20 и ξ2 = 18; длины участков l1 = l2 = 1000 м, абсолютная шероховатость Δ = 0,1 мм, температура воды t = 20℃.
Стоимость: 150 руб
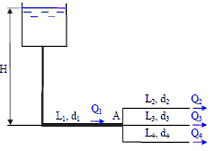
8. Трубопровод с расходом жидкости л/с в точке А разветвляется на два трубопровода: первый с размерами м и мм; второй с размерами м и мм. В точке В эти трубопроводы смыкаются. Во втором трубопроводе фильтр сопротивление которого эквивалентно трубе длиной . Определить расход и потерю давления в каждом трубопроводе, если плотность жидкости кг/м , а ее вязкость равна Ст.
9. Трубопровод с расходом жидкости л/с в точке А разветвляется на два параллельных одинаковых трубопровода длиной м и диаметром мм; в одном из них установлен дроссель с коэффициентом сопротивления . Считая режим течения турбулентным и приняв определить расходы в ветвях трубопровода и .
Стоимость: 120 руб
10. Определить при каком проходном сечении дросселя расходы в параллельных трубопроводах будут одинаковыми, если длины трубопроводов , . Их диаметры мм, коэффициент расхода дросселя . Расход рабочей жидкости перед разветвлением л/с, а ее вязкость Ст. Трубопровод считать гидравлически гладким.
Часть задач есть решенные, контакты