Гидравлика Р.152

Р.152

Задача 1.1

Вертикальный цилиндрический резервуар, расположенный на высоте h = 5 м над поверхностью земли, заполнен нефтью при температуре t = 0 °С. Определить поднятие уровня нефти в резервуаре Δh при повышении температуры на Δt = 30 °С. Коэффициент температурного расширения нефти β_t = 0,00072 1/°С.

Купить задачу 1.1

Задача 1.2

Бочка, заполненная бензином и не содержащая воздуха, нагрелась на солнце до t = 50ºС. На сколько повысилось бы давление бензина внутри бочки, если бы она была абсолютно жесткой? Начальная температура бензина t = 20ºС. Модуль упругости принять Е = 1 300 МПа, коэффициент температурного расширения β_t = 8·10^-4 град^-1.

Купить задачу 1.2

Задача 1.3

Минимальный свободный объем в системе объемного гидропривода для компенсации температурного расширения рабочей жидкости ΔV = 1,45 л. В процессе работы масло приобретает температуру t₂ = 60 °С. Емкость системы (объем масла после его нагревания) V = 40 л, β_t = 0,0009 град^-1. Какую температуру имеет масло при заполнении им гидропривода.

Купить задачу 1.3

Задача 1.4

Трубопровод длиною 400 м заполнен водой при атмосферном давлении. Требуется определить количество воды ΔV, которое необходимо дополнительно подать в трубопровод, чтобы давление в нем поднялось до значения p = 6370 кПа. Модуль упругости воды E = 1,96 · 10⁹ Н/м². Диаметр d = 300 мм.

Купить задачу 1.4

Задача 1.5

Для создания в рабочей камере, заполненной индустриальным маслом, модуль упругости которого Е = 1 389 МПа, избыточного давления р = 1 470 кПа используется плунжер. Первоначальный объем рабочей камеры V = 300 см3. Чему равен диаметр плунжера, если его переместили в рабочую камеру на 3 мм?

Купить задачу 1.5

Задача 1.6

Определить плотность и относительный вес жидкости, если ее удельный вес γ = 9 692 Н/м³.

Купить задачу 1.6

Задача 1.7

Удельный вес жидкости γ = 7,84 кН/м³. Определить ее динамический коэффициент вязкости, если вязкость, определенная при помощи прибора Энглера, равна 9,5 °Е.

Купить задачу 1.7

Задача 1.8

Определить динамический коэффициент вязкости жидкости и ее относительный вес, если вязкость, определенная при помощи прибора Энглера, равна 7,5 °Е. Удельный вес жидкости принять равным γ = 8,84 кН/м³.

Купить задачу 1.8

Задача 1.9

Определить повышение давления в закрытом объеме гидропривода, при повышении температуры масла от t₁ = 20°С до t₂ = 38°C, если коэффициент температурного расширения равен β_t = 7 · 10^-4 град^–1, коэффициент объемного сжатия β_р = 6,5 · 10^-4 Па^-1. Утечками жидкости и деформацией элементов конструкции объемного гидропривода пренебречь.

Задача 1.10

В цилиндрическом резервуаре высотой 6 м находится бензин (β_t = 0,0008ºС^-1). При температуре t₁ = 15ºС бензин не доходит до края на 10 см. Определить при какой температуре бензин начнет переливаться через край резервуара.

Купить задачу 1.10

Задача 2.1

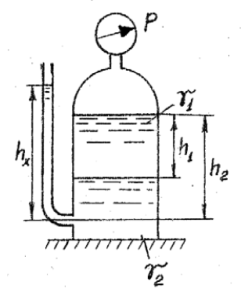
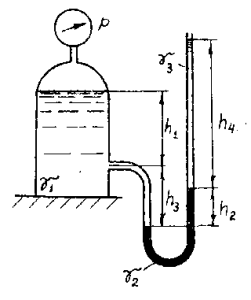
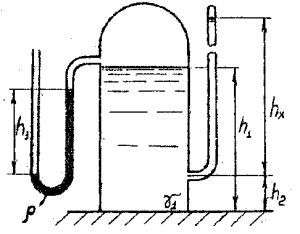
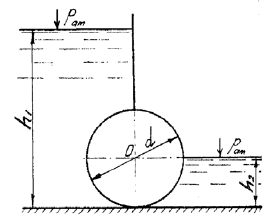
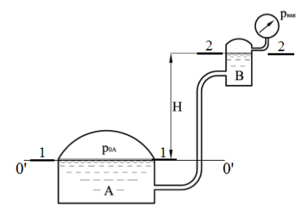
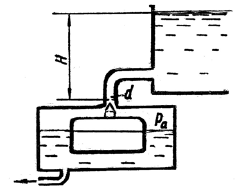
В геометрически закрытом сосуде налиты две не смешивающиеся жидкости (рис. 1. См. Приложение). Удельный вес жидкости, образующей верхний слой γ₁,, равен 8 кН/м³, толщина h₁ = 3 м. Удельный вес жидкости нижнего слоя γ₂ = 10 кН/м³. Открытый пьезометр присоединен на глубине h₂ = 5 м от свободной поверхности. Показание манометра p = 16 кПа. Определить высоту h_x, на которую поднимется жидкость в пьезометре.

Купить задачу 2.1

Задача 2.2

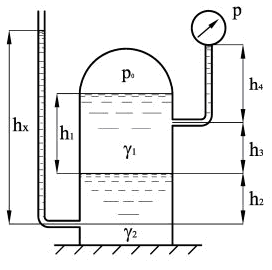
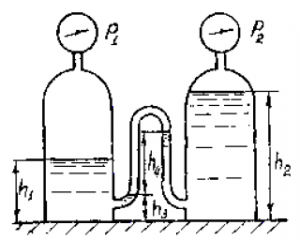
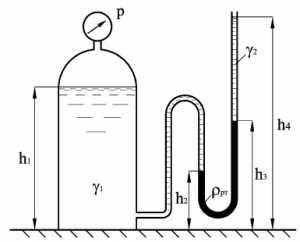
В герметически закрытом сосуде налиты две не смешивающиеся жидкости (рис. 2). Удельный вес жидкости, образующей верхний слой γ₁ = 9 кН/м³, толщина этого слоя h₁ = 4,0 м. Удельный вес жидкости нижнего слоя γ₂ = 11 кН/м³. Ниже линии раздела на глубине h₂ = 2,0 м присоединен открытый пьезометр. Выше линии раздела на величину h₃ = 2,0 м присоединен манометр на трубке, длина которой h₄ = 3,0 м.

Показание манометра p = 21 кПа. На какую высоту h_х поднимется жидкость в открытом пьезометре?

Купить задачу 2.2

Задача 2.3

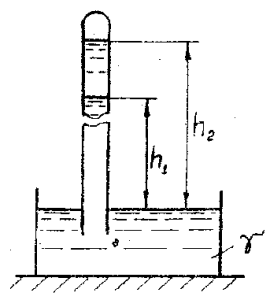
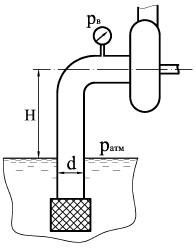
Запаянная с одного конца трубка, заполненная жидкостью, имеющей удельный вес γ, опрокинута не запаянным концом в открытый сосуд, заполненный той же жидкостью (рис. 3). При атмосферном давлении, равном 732 мм рт. ст., жидкость установится на высоте h₁ над уровнем свободной поверхности в сосуде. В случае повышения атмосферного давления до величины 769,48 мм рт. ст. высота уровня свободной поверхности в трубке над уровнем свободной поверхности в сосуде составит h₂. Определить удельный вес жидкости γ, если h₂ – h₁ = 500 мм, давление паров жидкости можно принять равным нулю, плотность ртути ρ_рт = 13 600 кг/м³.

Купить задачу 2.3

Задача 2.4

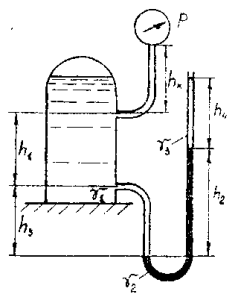
Герметически закрытый сосуд, заполненный жидкостью, имеет два патрубка (рис. 4). К верхнему присоединен манометр посредством соединительной трубки, к нижнему – изогнутая трубка, заполненная ртутью. Расстояние между патрубками h₁ = 1 м, разность уровней ртути h₂ = 1,5 м, уровень ртути в левой ветви изогнутой трубки находится ниже точки ее присоединения на h₃ = 1 м. Удельный вес жидкости, заполняющей сосуд, γ₁ = 10 кН/м³, удельный вес ртути γ₂ = 133,4 кН/м³. Определить длину соединительной трубки манометра, если его показания р = 185,1 кПа, а над ртутью в открытой ветви находится слой жидкости удельного веса γ₃ = 20 кН/м³, толщина слоя этой жидкости h₄ = 1 м.

Купить задачу 2.4

Задача 2.5

Герметичный сосуд, частично заполненный жидкостью удельного веса γ₁ = 10 кН/м³, имеет на крышке манометр (рис. 5). На глубине h₁ = 1 м от уровня свободной поверхности к сосуду присоединена изогнутая трубка, заполненная ртутью, удельный вес которой γ₂ = 133,4 кН/м³. Разность уровней ртути в изогнутой трубке h₂ = 0,5 м. Расстояние от точки присоединения изогнутой трубки до уровня ртути в ее левой ветви h₃ = 0,8 м. Выше уровня ртути в правой ветви налита жидкость, имеющая удельный вес γ₃ = 20 кН/м³, слоем h₄ = 2 м. Определить показания манометра p.

Купить задачу 2.5

Задача 2.6

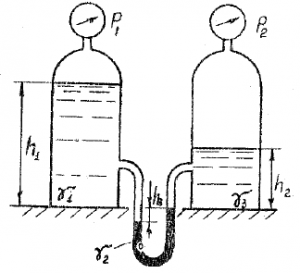
Два герметичных сосуда наполнены разнородными жидкостями с удельными весами γ1 = 10 кН/м3 и γ2 = 12 кН/м3 на высоту h1 = 1 м и h2 = 2 м (рис. 6). Они соединены изогнутой трубкой, частично заполненной жидкостью, находящейся в сосудах, частично воздухом. Высота свободной поверхности в левой ветви от уровня основания сосудов h3 = 0,4 м. Разность уровней жидкости в левой и правой ветвях h4 = 1 м. В верхних точках сосудов установлены манометры, показание первого манометра p1 = 5 кПа. Чему равно показание второго манометра p2?

Купить задачу 2.6

Задача 2.7

Два герметически закрытых сосуда установлены на одной горизонтальной плоскости и соединены изогнутой трубкой, в которой находится ртуть (рис. 7). Сосуды заполнены на высоту h₁ = 2 м и h₂ = 1 м жидкостями, имеющими удельные веса γ₁ = 10 кН/м³, γ₃ = 20 кН/м³ соответственно. Разность уровней ртути в изогнутой трубке h₃ = 0,2 м, удельный вес ртути γ₂ = 133,4 кН/м³. Определить показание манометра, аналогично расположенного на крышке первого сосуда p₁ = 100 кПа. Верхний край ртути совпадает с плоскостью оснований сосудов.

Купить задачу 2.7

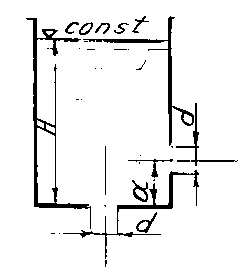
Задача 2.8

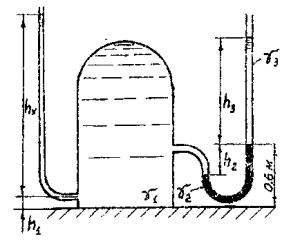
От герметичного сосуда, заполненного жидкостью удельного веса γ₁ = 10 кН/м³, на разной высоте отходит пьезометр и изогнутая трубка, частично заполненная ртутью (рис. 8). Пьезометр присоединен на высоте h1 = 0,1 м от дна сосуда. Перепад уровней ртути в изогнутой трубке h₂ = 0,3 м. Высота свободной поверхности ртути в правой ветви изогнутой трубки 0,6 м от дна сосуда. Удельный вес ртути γ₂ = 133,4 кН/м³. Определить высоту, на которую поднимется жидкость в пьезометре h_x, если над ртутью в изогнутой трубке находится слой жидкости толщиной h₃ = 1 м, удельный вес этой жидкости γ₃ = 12 кН/м³.

Купить задачу 2.8

Задача 2.9

Герметичный сосуд частично заполнен жидкостью с удельным весом γ₁ = 10 кН/м³ на высоту h₁ = 1 м. На высоте h₂ = 0,2 м от дна сосуда выведена трубка, из которой практически полностью откачан воздух (рис. 9). Выше уровня свободной поверхности жидкости в сосуде от него отведена изогнутая трубка, заполненная ртутью, имеющей плотность ρ = 13 600 кг/м³. Уровень ртути в правой ветви на h₃ = 0,5 м выше левой. Определить, на какую высоту поднимется жидкость в запаянной трубке, из которой откачан воздух, принимая давление паров жидкости равным нулю и атмосферное давление 100 кПа.

Купить задачу 2.9

 Задача 2.10

Герметически закрытый сосуд (рис. 10) наполнен жидкостью с удельным весом γ1 до высоты h1 = 2 м. Избыточное давление в верхней части сосуда, измеренное манометром, p = 100 кПа. От сосуда отходит изогнутая трубка, заполненная жидкостью с удельным весом γ1, ртутью (ρрт = 13600 кг/м3) и жидкостью с удельным весом γ2 = 12 кН/м3. Высота уровней жидкостей в трубке h2 = 0,8 м, h3 = 1,5 м, h4 = 3,5 м. Определить удельный вес жидкости γ1.

Купить задачу 2.10

Задача 3.1

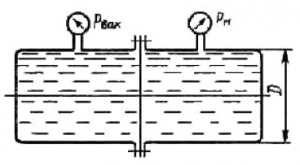
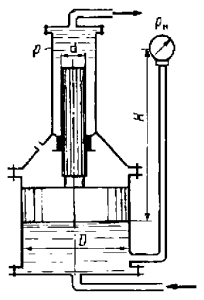
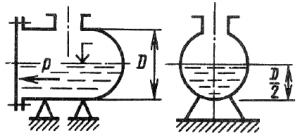
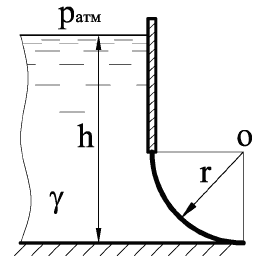
Определить значение силы, действующей на перегородку, которая разделяет бак, если ее диаметр D = 0,4 м, показания вакуумметра pвак = 0,065 МПа и манометра pм = 0,08 МПа (рис. 11).

Купить задачу 3.1

Задача 3.2

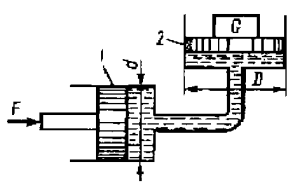
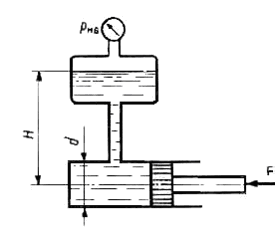
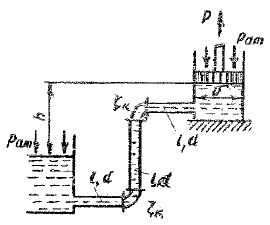
Определить давление в гидросистеме и вес груза G, лежащего на поршне 2, если для его подъема к поршню I приложена сила F = 1,8 кН (рис. 12). Диаметры поршней: D = 255 мм, d = 68 мм. Разностью высот пренебречь.

Купить задачу 3.2

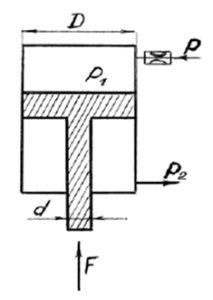
Задача 3.3

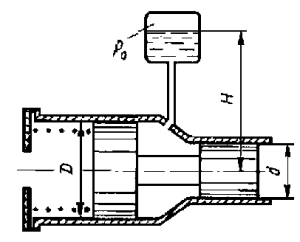
Определить давление р₁ жидкости, которую необходимо подвести к гидроцилиндру, чтобы преодолеть усилие, направленное вдоль штока F = 0,85 кН (рис. 13). Диаметры: цилиндра D = 41 мм, штока d = 16 мм. Давление в бачке р₀ = 41 кПа, высота Н₀ = 4,55 м. Силу трения не учитывать. Плотность жидкости ρ = 1 000 кг/м³.

Купить задачу 3.3

Задача 3.4

Определить давление р в верхнем цилиндре гидропреобразователя (мультипликатора), если показание манометра р_м, присоединенного к нижнему цилиндру, равно 0,35 МПа (рис. 14). Поршни перемешаются вверх, причем сила трения составляет 10 % от силы давления жидкости на нижний поршень. Вес поршней G = 3,7 кН. Диаметры поршней: D = 370 мм, d = 75 мм; высота Н = 2,0 м; плотность масла ρ = 900 кг/м³.

Купить задачу 3.4

Задача 3.5

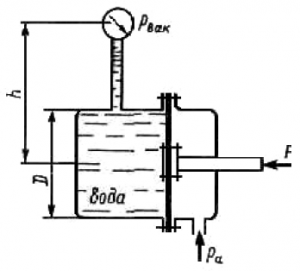
Определить показание мановакуумметра p_мв, если к штоку поршня приложена сила F = 0,95 кН, его диаметр D = 85 мм, высота Н = 0,98 м, плотность жидкости ρ = 800 кг/м³ (рис. 15).

Купить задачу 3.5

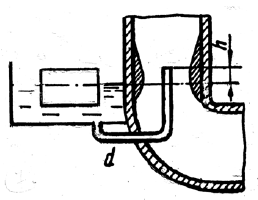
Задача 3.6

Определить силу F, действующую на шток гибкой диафрагмы, если ее диаметр D = 180 мм, показание вакуумметра p_вак = 0,03 МПа, высота h = 0,8 м (рис. 16). Площадью штока пренебречь. Найти абсолютное давление в левой полости, если h_а = 760 мм рт. ст.

Купить задачу 3.6

Задача 3.7

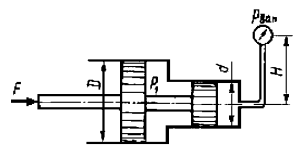
Определить силу F на штоке золотника, если показание вакуумметра р_вак = 43 кПа, избыточное давление р₁ = 0,68 МПа, высота Н = 2,65 м, диаметры поршней D = 60 мм и d = 17 мм, ρ = 990 кг/м³ (рис. 17).

Купить задачу 3.7

Задача 3.8

Система из двух поршней, соединенных штоком, находятся в равновесии (рис. 18). Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке, — масло с плотностью ρ = 850 кг/м³. Диаметры: D = 63 мм; d = 20 мм; высота Н = 950 мм; избыточное давление р₀ = 8,1 кПа.

Купить задачу 3.8

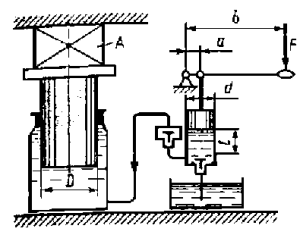
Задача 3.9

Давление в цилиндре гидравлического пресса повышается в результате нагнетания в него жидкости ручным поршневым насосом и сжатия ее в цилиндре (рис. 19). Определить число двойных ходов n поршня ручного насоса, необходимое для увеличения силы прессования детали А от 0 до 0,8 МН, если диаметры поршней: D = 455 мм, d = 8,0 мм; ход поршня ручного насоса L = 22 мм; объемный модуль упругости жидкости E = 1 200 мПа; объем жидкости в прессе V = 50 л. Чему равно максимальное усилие F на рукоятке насоса при ходе нагнетания, если b/а = 8,5?

Купить задачу 3.9

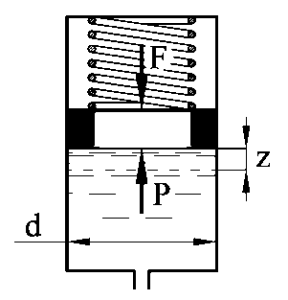
Задача 3.10

Определить жесткость пружины с, если под давлением жидкости р = 1,2 МПа поршень пружинного гидроаккумулятора диаметром d = 200 мм во время зарядки поднялся вверх на высоту z = 10 см (рис. 20).

Купить задачу 3.10

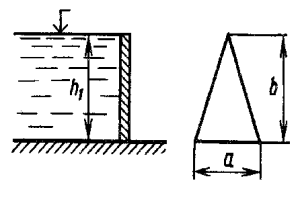
Задача 4.1

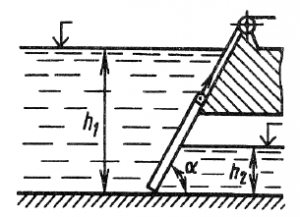
Шлюзовое окно закрыто щитом треугольной формы, ширина которого а = 1,5 м, а высота b = 4 м (рис. 31). За щитом воды нет, а глубина воды перед ним h₁ = 4 м, при этом горизонт воды перед щитом совпадает с его вершиной. Определить силу абсолютного гидростатического давления на щит и положение центра давления. Удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 4.1

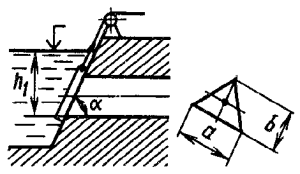
Задача 4.2

Плоский квадратный щит установлен с углом наклона к горизонту α = 45° (рис. 32). Глубина воды перед щитом – h₁ = 6 м, за щитом h₂ = 1,5 м, ширина щита b = 4 м. Определить силу избыточного гидростатического давления и центр давления жидкости на щит. Удельный вес воды γ_в = 9,81 кН/м³.

Купить задачу 4.2

Задача 4.3

Для сброса излишков воды используют донный водовыпуск, прямоугольный затвор которого имеет размеры а = 1,2 м и b = 2 м (рис. 33). Глубина воды от ее свободной поверхности до нижней кромки затвора h₁ = 10 м, угол наклона затвора α = 60°, плотность воды ρ = 1 000 кг/м³. Определить силу абсолютного гидростатического давления жидкости на затвор водовыпуска.

Купить задачу 4.3

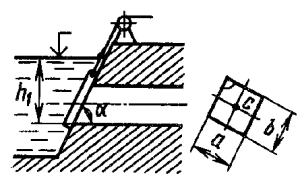
Задача 4.4

Затвор донного водовыпуска треугольной формы имеет ширину а = 1,2 м и высоту b = 1,5 м (рис. 34). Угол наклона затвора α = 45°, нижняя кромка затвора находится в воде на глубине h₁ = 9,5 м, плотность воды ρ = 1 000 кг/м³. Определить силу абсолютного гидростатического давления жидкости и положение центра давления на затвор.

Купить задачу 4.4

Задача 4.5

Цистерна диаметром D = 1,2 м наполовину заполнена керосином (рис. 35). Определить силу избыточного гидростатического давления P, которую необходимо приложить для открытия крышки цистерны, а также найти координату точки приложения этой силы. Плотность керосина ρ_к = 830 кг/м³.

Купить задачу 4.5

Задача 4.6

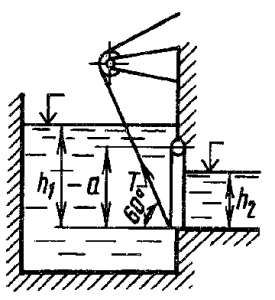
Отверстие шлюза-регулятора перекрыто плоским металлическим затвором с размерами: высота a = 4 м, ширина b = 2 м и толщина c = 0,25b (рис. 36). Глубина воды слева от затвора h1 = 3 м, а справа h2 = 1,5 м. Определить равнодействующую силы давления воды на затвор и положение центра ее приложения, начальную силу тяги, необходимую для открытия затвора. Коэффициент трения скольжения f = 0,4, удельный вес материала, из которого изготовлен затвор, γз = 11 кН/м3, воды γв = 9,81 кН/м3.

Купить задачу 4.6

Задача 4.7

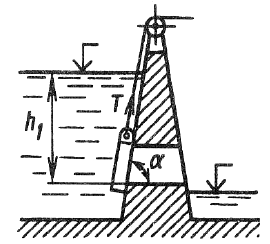
Прямоугольный щит перекрывает отверстие в теле плотины. Щит установлен с углом наклона α = 70°, имеет высоту a = 2 м, ширину b = 1,6 м и толщину c = 0,25b (рис. 37). Нижняя кромка щита находится в воде на глубине h1 = 10 м, масса щита m = 2 т. Определить силу тяги T, которая необходима для поднятия щита вверх, принимая коэффициент трения скольжения его направляющих f = 0,3. Удельный вес воды γв = 9,81 кН/м3.

Купить задачу 4.7

Задача 4.8

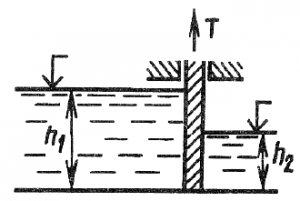
Плоский прямоугольный щит перекрывает выходное отверстие резервуара (рис. 38). Щит имеет размеры а = 3 м х b = 4 м, вес G = 26 кН. Глубина воды перед щитом от свободной поверхности воды до нижней его кромки h₁ = 5 м, за щитом h₂ = 2 м. Удельный вес воды γ_в = 9,81 кН/м³. Трением в шарнирах пренебречь. Определить начальную силу тяги Т троса, необходимую для открывания щита.

Купить задачу 4.8

Задача 4.9

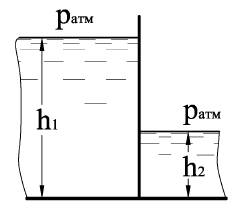
Промежуточная вертикальная стенка делит емкость (рис. 39) шириной b = 1,2 м на два отсека. Определить значение равнодействующей сил избыточного гидростатического давления на эту стенку и точку ее приложения, а также точки приложения сил P₁ и P₂, если уровень воды в левом отсеке h₁ = 1200 мм, а в правом – h₂ = 480 мм.

Купить задачу 4.9

Задача 4.10

Определить силу давления масла (γ = 8650 Н/м³) на болты крышки (рис. 40), которая имеет форму прямоугольника высотой a = 0,64 м и шириной b = 1,5 м. Показание манометра р_м = 120 кПа, высота h = 2 м.

Купить задачу 4.10

Задача 5.1

Определить равнодействующую силу гидростатического давления жидкости на цилиндрическую поверхность аb радиусом r и шириной b (рис. 41), если: r = 0,4 м; b = 1,4 м; h = 2,2 м; ρ = 1 000 кг/м³; р_о = 40 кПа.

Купить задачу 5.1

Задача 5.2

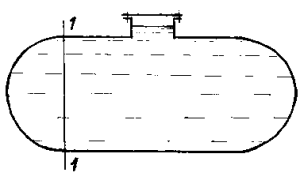
Определить силы Р_х и Р_z, стремящиеся разорвать торцовую, полусферическую части цистерны диаметром D = 3 м, заполненной нефтью с удельным весом 7 850 н/м³, по сечениям 1 – 1 и 2 – 2 (рис. 42). Уровень нефти находится на высоте h = 0,5 м над цилиндрической.

Купить задачу 5.2

Задача 5.3

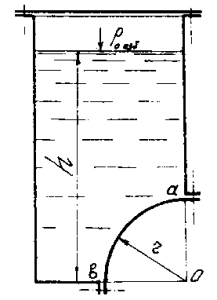
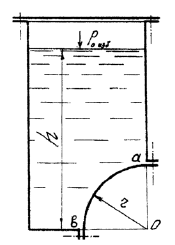
В нижней части вертикальной плоской стенки открытого резервуара имеется проем прямоугольной формы шириной b = 2,0 м, закрытый криволинейной крышкой АВ в виде четверти боковой поверхности цилиндра радиусом r = 1,0 м (рис 43). Глубина воды в резервуаре h = 2,0 м. Определить величину и направление действия силы P давления воды на крышку.

Купить задачу 5.3

Задача 5.4

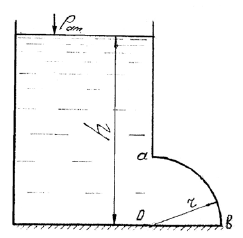
Затвор донного водовыпуска треугольной формы имеет ширину a = 1,2 м и высоту b = 1,5 м (рис. 44). Угол наклона затвора α = 45°, нижняя кромка затвора находится в воде на глубине h₁ = 9,5 м, плотность воды ρ = 1000 кг/м³. Определить силу абсолютного гидростатического давления жидкости и положение центра давления на затвор.

Купить задачу 5.4

Задача 5.5

Определить величину и направление действия равнодействующей силы давления воды на цилиндрический затвор диаметром d = 2,0 м, перегораживающий прямоугольный канал шириной b = 5,0 м, если глубина h₁ = 3,0 м, h₂ = 1,0 м (рис. 45).

Купить задачу 5.5

Задача 5.6

Определить равнодействующую силу гидростатического давления жидкости на цилиндрическую поверхность ab радиусом r и шириной b (рис. 46), если: r = 0,6 м; b = 2,0 м; h = 2,5 м; ρ = 800 кг/м³; p_о = 15 кПа.

Купить задачу 5.6

Задача 5.7

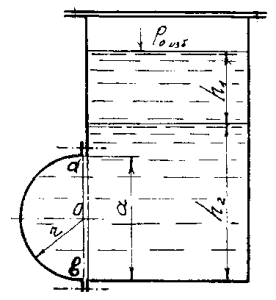
В герметично закрытый резервуар налиты вода, глубина которой h₂ = 1,6 м, и масло, слой которого составляет h₁ = 0,5 м, при плотности ρ = 800 кг/м³ (рис. 47). На свободной поверхности масла действует избыточное давление р_о = 15 кПа. Определить силу давления на цилиндрическую крышку аb радиусом r = 0,7 м, закрывающую прямоугольное отверстие высотой а = 1,4 м и шириной b = 1,2 м.

Купить задачу 5.7

Задача 5.8

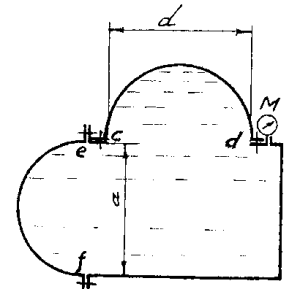
Определить силы давления воды на полуцилиндрическую крышку ef, закрывающую прямоугольное отверстие высотой h = 0,8 м и шириной b = 1,6 м, и на полусферическую крышку cd, закрывающую круглое отверстие диаметром d = 1,0 м, если манометр М показывает давление р_ман = 40 кПа (рис. 48).

Купить задачу 5.8

Задача 5.9

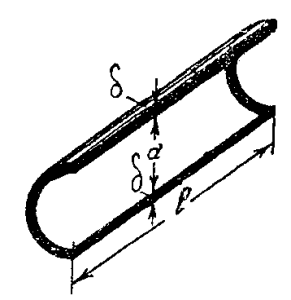
Найти минимальную толщину δ стенок стальной трубы диаметром d = 25 мм, если давление жидкости p = 10 МПа, а допускаемое напряжение на растяжение для стали G = 150 МПа (рис. 49). Весом жидкости пренебречь.

Купить задачу 5.9

Задача 5.10

Секторный затвор (рис. 50) радиусом r = 1,2 м закрывает донное отверстие прямоугольной формы в плотине. Определить значение и направление действия силы избыточного давления воды на затвор, если напор на плотине h = 5 м, ширина отверстия b = 2,5 м.

Купить задачу 5.10

Задача 6.1

Индустриальное масло ИС-30, температура которого 20°С поступает от насоса в гидроцилиндр по трубопроводу d = 22 мм. Определить режим течения масла, а также температуру, при которой ламинарный режим сменяется турбулентным, если подача насоса Q = 105 л/мин.

Купить задачу 6.1

Задача 6.2

Определить критическую скорость, отвечающую переходу от ламинарного режима к турбулентному, в трубе диаметром d = 0,03 м при движении воды и воздуха, при температуре 25°С и глицерина при температуре 20°С.

Купить задачу 6.2

Задача 6.3

Определить число Рейнольдса и режим движения воды в водопроводной трубе диаметром d =300 мм, если протекающий по ней расход Q = 0,136 м³/с. Температура воды 10°С.

Купить задачу 6.3

Задача 6.4

Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d = 12 мм, максимальный диаметр d = 3500 мм. Расчетные скорости движения воды в них равны 0,5 … 4 м/с. Определить минимальное и максимальное значения чисел Рейнольдса и режим течения воды в этих трубопроводах.

Купить задачу 6.4

Задача 6.5

Конденсатор паровой турбины, установленный на тепловой электростанции, оборудован 8 186 охлаждающими трубками диаметром d = 0,025 м. В нормальных условиях работы через конденсатор пропускается 13 600 м³/с циркуляционной воды с температурой 12,5…13°С. Будет ли при этом обеспечен турбулентный режим движения в трубках?

Задача 6.6

Как изменяется число Рейнольдса при переходе трубопровода от меньшего диаметра к большему и при сохранении постоянного расхода Q = const?

Купить задачу 6.6

Задача 6.7

По трубопроводу диаметрам d = 100 мм транспортируется нефть. Определить критическую скорость, соответствующую переходу ламинарного движения в турбулентное, и возможный режим движения нефти.

Купить задачу 6.7

Задача 6.8

Горизонтальный отстойник для осветления сточных вод представляет собой удлиненный прямоугольный в плане резервуар. Глубина его h = 2,5 м, ширина b = 6 м. Температура воды 20°С. Определить среднюю скорость и режим движения сточной жидкости, если ее расчетный расход Q = 0,08 м³/с. При какой скорости движения жидкости в отстойнике будет наблюдаться ламинарный режим движения жидкости?

Купить задачу 6.8

Задача 6.9

Циркуляция масла системы смазки двигателя внутреннего сгорания происходит следующим образом: из бака масло при температуре t₁ = 60 °C подается по трубе d₁ = 40 мм в двигатель, в двигателе масло нагревается до температуры t₂ = 100 °C и по трубе d₂ = 30 мм направляется в радиатор, а затем, после охлаждения, – обратно в бак.

Определить числа Рейнольдса и режимы течения масла перед входом в двигатель и на выходе из двигателя, если расход циркулирующего в системе масла Q = 1,25 л/с.

Купить задачу 6.9

Задача 6.10

Глицерин, скипидар и этиловый спирт текут по трубам прямоугольного сечения 100 мм × 50 мм с расходом 12 л/с. Определить число Рейнольдса для каждой жидкости, если кинематическая вязкость глицерина – 1,059 Ст, скипидара – 0,0183 Ст, этилового спирта – 0,0154 Ст.

Купить задачу 6.10

Задача 7.1

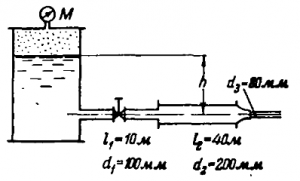
Определить высоту h, на которую вода из сосуда поднимается по трубе (рис. 51) при следующих исходных данных: диаметр трубопровода d₁ = 125 мм, диаметр горловины d₂ = 75 мм, расход Q = 15 л/с, избыточное давление в сечении 1–1 p_м1 = 3050 Па. При расчете потерями напора пренебречь.

Купить задачу 7.1

Задача 7.2

Пренебрегая потерями напора, определить диаметр горловины d₂ (см. рис. 51), чтобы при пропуске расхода воды по трубопроводу Q = 10,1 л/с вода по трубке подсасывалась на высоту h = 60 см. Диаметр трубопровода d1 = 100 мм и избыточное давление в сечении 1 – 1 р_м = 6 533 Па.

Купить задачу 7.2

Задача 7.3

Определить напор H, который необходимо поддерживать в резервуаре, чтобы расход воды, пропускаемый по наклонному трубопроводу диаметром d = 100 мм и длиной l = 60 м, составлял не менее 16 л/с. Выходное сечение трубопровода расположено на расстоянии a = 1,3 м ниже входного, эквивалентная шероховатость труб Δ_э = 0,2 мм, кинематический коэффициент вязкости воды ν = 0,0131 см²/с. Местными потерями и скоростным напором в резервуаре пренебречь.

Купить задачу 7.3

Задача 7.4

По трубопроводу длиной 3,5 км и диаметром d = 250 мм перекачивается жидкость с расходом Q = 70 л/с. Определить потери напора в трубопроводе, если кинематическая вязкость жидкости ν = 1,31 сСт. Трубы стальные бывшие в эксплуатации Δ_э = 0,15 мм.

Купить задачу 7.4

Задача 7.5

Определить длину горизонтальной прямой трубы, по которой в количестве Q = 31,4 л/с прокачивается мазут (ν = 2000 мм²/с при 20 °С), если внутренний диаметр трубы d = 0,25 м, а потери напора на рассматриваемом участке равны h_l = 2,3 м.

Купить задачу 7.5

Задача 7.6

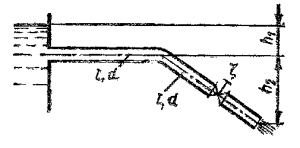
На какой высоте от уровня воды в источнике (рис. 52) должен быть установлен центробежный насос, чтобы вакуум во всасывающем патрубке насоса не превышал 5,6 м? Подача насоса Q = 7 л/с, диаметр всасывающего трубопровода и патрубка d = 120 мм, общие потери напора во всасывающей линии составляют 0,75 м.

Купить задачу 7.6

Задача 7.7

По трубопроводу, соединяющему два цилиндрических резервуара А и В, подается вода (ρ = 1000 кг/м³) на высоту H = 10 м (рис. 52). Показание вакуумметра, установленного в резервуаре В, р_вак = 45 кПа. Какое избыточное давление необходимо создать в резервуаре А для подачи Q = 540 л/с, если общие потери напора составляют 12 м, диаметры резервуаров d_А = 5 м, d_В = 0,3 м?

Купить задачу 7.7

Задача 7.8

По наклонному трубопроводу диаметром d = 200 мм подают воду с расходом Q = 35 л/с. Давление воды в начальном сечении трубопровода p₁ = 200 кПа, коэффициент Дарси λ = 0,0225. Определить давление во втором сечении, расположенном на расстоянии l = 400 м от начального, учитывая, что центр тяжести второго сечения расположен на Δz = 4 м выше центра начального сечения.

Купить задачу 7.8

Задача 7.9

Потери напора при внезапном расширении потока в горизонтальном трубопроводе равны h = 0,4 м. Определить диаметр трубопровода d₁ перед внезапным расширением трубопровода до диаметра d₂ = 100 мм, если расход Q = 5 л/с.

Купить задачу 7.9

Задача 7.10

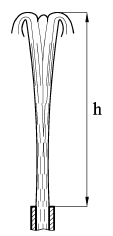
На какую высоту поднимется струя воды, вытекающая из трубопровода вертикально вверх (рис. 53), если скорость воды в выходном сечении равна 16 м/с? Сопротивлением струи о воздух пренебречь.

Купить задачу 7.10

Задача 8.1

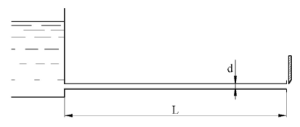
Вода сливается из бака А в бак В по трубопроводу, диаметр которого d = 80 мм и полная длина L = 2l = 10 м. Из бака В вода вытекает в атмосферу через цилиндрический насадок такого же диаметра d = 80 мм (коэффициент расхода μ = 0,82). Коэффициенты сопротивления колена и вентиля в трубе ζ_к = 0,3 и ζ_в = 4; коэффициент сопротивления трения λ = 0,03.

Определить, какой напор H нужно поддерживать в баке А, чтобы уровень в баке В находился на высоте h = 1,5 м.

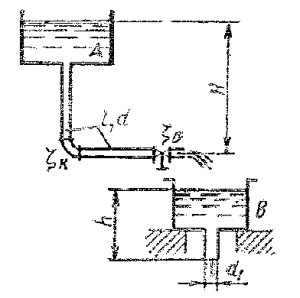
Купить задачу 8.1

Задача 8.2

По сифонному трубопроводу, для которого задан напор H = 6 м, необходимо подавать расход воды Q = 50 л/с при условии, чтобы вакуумметрическая высота в сечениях не превышала 7 м.

Опасное сечение С расположено выше начального уровня воды на h = 4 м, длина восходящей линии трубопровода до этого сечения l₁ = 100 м, а нисходящей линии l₂ = 60 м. Трубопровод снабжен приемным клапаном с сеткой (ζ_к = 5) и задвижкой.

Определить диаметр трубопровода d и коэффициент сопротивления задвижки ζ, удовлетворяющие условиям задачи. Потерями на поворотах пренебречь.

Купить задачу 8.2

Задача 8.3

Поршень диаметром D = 200 мм движется равномерно вверх в цилиндре, засасывая воду из открытого резервуара с постоянным уровнем. Диаметр трубопровода d = 50 мм; длина каждого из трех его участков l = 4 м; коэффициент сопротивления каждого колена ξ_к = 0,5; коэффициент сопротивления трения λ = 0,03. Когда поршень находится выше уровня в резервуаре на h = 2 м, потребная сила для его перемещения равна Р = 2 350 Н. Определить скорость подъема поршня. Весом поршня, трением его о стенки и потерями напора в цилиндре пренебречь.

Купить задачу 8.3

Задача 8.4

Вода вытекает в атмосферу из резервуара с постоянным уровнем по трубопроводу диаметром d = 100 мм, состоящему из горизонтального и наклонного участков одинаковой длины l = 50 м. Горизонтальный участок заглублен под уровень на h₁ = 2 м, наклонный участок имеет высоту h₂ = 25 м. Каков должен быть коэффициент сопротивления ξ задвижки, установленной в наклонном участке трубопровода, чтобы вакуумметрическая высота в конце горизонтального участка не превосходила 7 м? Какой расход будет при этом в трубопроводе? Коэффициент сопротивления трения принять равным λ = 0,035, потерю напора на повороте не учитывать.

Купить задачу 8.4

Задача 8.5

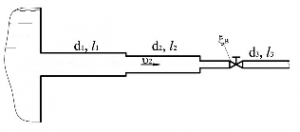
Определить потери напора h_w для трубопровода с диаметрами участков d₁ = 110 мм, d₂ = 65 мм, d₃ = 50 мм и длинами l₁ = 5 м, l₂ = 3 м, l₃ = 1 м, если коэффициент местного сопротивления вентиля ξ_в = 3, скорость воды на втором участке трубопровода υ₂ = 3,1 м/с. Коэффициент гидравлического трения принять λ = 0,065 (рис. 58).

Купить задачу 8.5

Задача 8.6

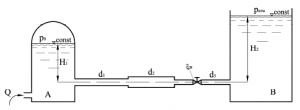
Вода, находящаяся под избыточным давлением p₀ = 80 кПа, из емкости A перетекает по трубе с диаметрами d₁ = 60 мм, d₂ = 30 мм в приемную емкость B (рис. 59). Определить расход Q в трубе, если высота Н = 6 м, коэффициент сопротивления крана ξ = 8, радиусы плавных изгибов трубы 120 мм. Потерями напора по длине пренебречь.

Купить задачу 8.6

Задача 8.7

Вода перетекает из напорного бака А в резервуар B по трубе, состоящей из трех участков с диаметрами d₁ = 50 мм, d₂ = 70 мм, d₃ = 40 мм (рис. 60). Пренебрегая потерями напора на трение по длине, определить расход, если высоты H₁ = 1,5 м, H₂ = 13,5 м; избыточное давление в напорном баке p₀ = 0,15 МПа, коэффициент сопротивления вентиля ξ_в = 5.

Купить задачу 8.7

Задача 8.8

Вода из водонапорной башни поступает к потребителю по трубопроводу диаметром d = 75 мм. Определить длину участка трубопровода l при котором расход воды будет Q = 2 л/с, если вертикальное расстояние от уровня воды в водонапорной башне до центра выходного сечения трубы 30 м, эквивалентная шероховатость трубы Δ = 0,1 мм, температура воды 10 °С. Местными потерями и скоростным напором на выходе из трубы пренебрегаем.

Купить задачу 8.8

Задача 8.9

Для горизонтального трубопровода, размеры которого указаны на схеме, определить расход Q при заданном избыточном давлении p = 0,4 МПа и уровне воды в резервуаре h = 5 м. Коэффициенты сопротивления вентиля ζ_вен = 4 и сопла ζ_с = 0,06 (сжатие струи на выходе из сопла отсутствует). Шероховатость каждого из участков трубопровода Δ_э = 1 мм (старые водопроводные трубы).

Купить задачу 8.9

Задача 8.10

По трубопроводу длиной 3 км и d = 200 мм перекачивается жидкость с расходом Q = 60 л/с. Определить потери напора в трубопроводе, если кинематическая вязкость жидкости ν = 1,31 сСт. Трубы стальные бывшие в эксплуатации Δ_э = 0,15 мм.

Купить задачу 8.10

Задача 9.1

Определить утечку воды из тепловой сети через образовавшееся в результате аварии отверстие в стенке трубопровода, если избыточное давление в сети p_изб = 4,4 атм, площадь отверстия 1 см², а коэффициент расхода отверстия μ = 1, плотность горячей воды 978 кг/м³.

Купить задачу 9.1

Задача 9.2

В резервуаре, наполненном бензином на высоту Н = 2 м, имеются два круглых отверстия диаметром d = 10 cм. Одно отверстие расположено в вертикальной боковой стенке на расстоянии а = 0,5 м от дна, другое – в центре дна. Определить суммарный расход из отверстий, если отметка уровня бензина поддерживается постоянной.

Купить задачу 9.2

Задача 9.3

В дне цилиндрического резервуара, площадью поперечного сечения Ω = 7,5 м², находится отверстие с острыми кромками площадью ω = 0,05 м². Глубина воды в резервуаре h = 5 м. За сколько времени из резервуара вытечет половина имеющегося объема воды?

Купить задачу 9.3

Задача 9.4

В поршневую полость гидроцилиндра подводится масло (ρ = 895 кг/м³) через дроссель диаметром d₀ = 1,5 мм. Давление перед дросселем р = 12,5 МПа, давление на сливе р₂ = 200 кПа, усилие на штоке F = 20 кН, диаметр поршня D = 100 мм, диаметр штока d = 40 мм. Определить скорость перемещения поршня, движущегося равномерно, если коэффициент расхода дросселя μ = 0,62. Весом поршня и штока, трением в гидроцилиндре и утечками масла пренебречь.

Купить задачу 9.4

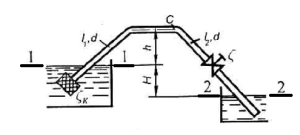
Задача 9.5

Определить количество воды, поступающее в корпус судна через пробоину площадью 0,1 м² в течение часа, если центр пробоины расположен на 5 м ниже уровня воды за бортом, приняв коэффициент расхода μ = 0,6.

Купить задачу 9.5

Задача 9.6

Определить расход и скорость воды, вытекающей из бассейна через отверстие диаметром d = 100 мм в стенке, если уровень воды находится на высоте H = 5 м над центром отверстия. Как изменятся расход и скорость истечения, если к отверстию подключить: 1) внешний цилиндрический насадок; 2) внутренний цилиндрический насадок; 3) коноидальный насадок?

Купить задачу 9.6

Задача 9.7

Бензин поступает к жиклеру из поплавковой камеры благодаря вакууму, который создается в диффузоре карбюратора. Выходное сечение бензотрубки расположено на h = 5 мм выше уровня бензина в поплавковой камере, вакуум в диффузоре р_вак = 15 кПа, давление в поплавковой камере атмосферное.

Пренебрегая потерями напора, определить расход бензина (ρ = 720 кг/м³) через жиклер диаметром d = 1 мм при коэффициенте расхода μ = 0,8.

Купить задачу 9.7

Задача 9.8

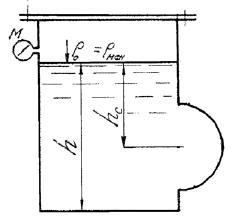
Истечение жидкости из герметически закрытого резервуара в атмосферу происходит при постоянном напоре Н = 5 м через внешний цилиндрический насадок диаметром d = 10 см. Какое давление необходимо создать на свободной поверхности воды в резервуаре, чтобы расход при истечении не превышал 60 л/с?

Купить задачу 9.8

Задача 9.9

Определить диаметр отверстия в диафрагме, при котором из топливного бака в поплавковую камеру карбюратора будет поступать расход бензина Q = 8 см³/с при напоре H = 0,4 м, приняв коэффициент расхода отверстия μ = 0,65.

Купить задачу 9.9

Задача 9.10

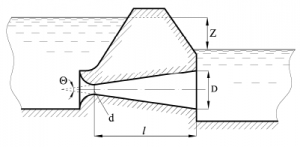
Донный водовыпуск длиной l = 4 м имеет форму конически расходящегося насадка с углом конусности Θ = 7° и работает в затопленном режиме (рис. 66). Определить диаметры в начале и конце водовыпуска, если расход Q = 0,54 м³/с, разность отметок уровней z = 0,3 м.

Купить задачу 9.10

Задача 10.1

Определить напряжение σ в стенках свинцового трубопровода (Е = 4,9 · 10³ МПа) длиною 1,5 км при времени закрытия задвижки 25 с. Начальное избыточное давление керосина (Е₀ = 1,37 · 10³ МПа) в трубопроводе 7,4 Н/см², расход керосина 5,75 л/с, D = 200 мм, толщина стенки трубопровода 23 мм.

Купить задачу 10.1

Задача 10.2

В гидросистеме отключение потребителя производится электромагнитным краном. Кран полностью перекрывает трубопровод за время t = 0,02 с. Определить повышение давления перед краном в момент отключения потребителя при следующих данных. Длина трубопровода от крана до гидроаккумулятора, где гасится ударное давление, L = 4 м, диаметр трубопровода 12 мм, толщина его стенки 1 мм, материал – сталь (Е = 2,2 · 10⁵ МПа), объемный модуль упругости жидкости АМГ-10 Е₀ = 1,33 · 10³ МПа, ее плотность 900 кг/м³, скорость движения жидкости в трубе 4,5 м/с.

Купить задачу 10.2

Задача 10.3

Трубопровод, подключенный к баку с водой и имеющий размеры L = 20 м и d = 50 мм, мгновенно закрывается. Определить скорость распространения ударной волны и величину ударного повышения давления, если толщина стенок трубы 6 мм и материал ее – сталь (Е = 2 · 10⁵ МПа). Модуль упругости воды Е₀ = 2 · 10³ МПа, расход воды до закрытия трубопровода Q = 2 л/с.

 

Купить задачу 10.3

Задача 10.4

Определить максимально допустимый расход воды в чугунном трубопроводе (Е = 9,81 · 10⁴ МПа), чтобы максимальное давление при времени закрытия затвора 0,5 с не превышало 13 500 кН/м². Диаметр трубопровода 300 мм, его длина 450 м, толщина стенок 5 мм.

Купить задачу 10.4

Задача 10.5

Смазка параллелей ползуна производится из масленки под избыточным давлением р₀ = 0,5 МПа по трубке диаметром 6 мм и длиной 2 м через отверстие, периодически открываемое ползуном. Определить повышение давления в трубке, если толщина ее стенок δ = 2 мм и она выполнена из стали (Е = 1,2 · 10⁵ МПа), модуль упругости масла Е₀ = 1,5 · 10³ МПа, ρ = 870 кг/м³, ползун перемещается со скоростью V = 2 м/с.

Примечание: истечение масла из отверстия рассматривать как истечение из цилиндрического насадка (коэффициент скорости φ = 0,82).

Купить задачу 10.5

Задача 10.6

По бетонному трубопроводу (Е = 19,62 · 10³ МПа), имеющему от напорного резервуара до затвора длину 1 574 м, диаметр 150 мм, толщину стенок 30 мм, проходит вода в количестве 0,09 м³/с. Начальное избыточное давление перед затвором 13,52 Н/см². При внезапном закрытии затвора, расположенного в конце трубопровода, какое будет давление у затвора и через какое время это давление распространится до напорного резервуара?

Купить задачу 10.6

Задача 10.7

Вода течет из бака по трубопроводу длиною 40 м, диаметром 30 мм и толщиной стенок 3 мм, в конце трубопровода установлена задвижка. Минимальное время закрытия задвижки 0,07 с. Перед задвижкой установлено устройство для гашения гидравлического удара с диаметрами d = 30 мм и D = 100 мм. Определить давление воздуха в устройстве для гашения гидравлического удара, если расход истечения 7 л/с, материал трубопровода сталь (Е = 2 · 10⁵ МПа), модуль упругости воды Е₀ = 2 · 10³ МПа.

Купить задачу 10.7

Задача 10.8

Определить скорость распространения ударной волны и повышение давления в бетонном трубопроводе (Е = 19,62 · 10³ МПа) при мгновенном закрытии задвижки. Диаметр трубопровода 120 мм, толщина стенки 25 мм, расход воды (Е₀ = 2 · 10³ МПа) в трубопроводе 0,95 л/с.

Купить задачу 10.8

Задача 10.9

Определить диаметр чугунного трубопровода (Е = 9,81 · 10⁴ МПа), чтобы при расходе 10 л/с максимальное давление при времени закрытия затвора 5,6 с не превышало 10 900 кПа. Длина трубопровода 1 450 м, толщина стенок 10 мм.

Купить задачу 10.9

Задача 10.10

Из напорного резервуара по чугунному трубопроводу длиной 300 м поступает нефть в количестве Q = 0,023 м³/с. Диаметр трубопровода d = 200 мм, толщина стенок δ = 6 мм. Определить максимальное давление в трубопроводе при закрытии задвижки установленной в конце трубопровода, если время ее закрытия t_з = 10 с, начальное давление p₀ = 127,5 кПа. Произойдет ли в этом случае разрушение трубопровода ([σ] = 35 МПа)?