ТТ.137
МСХА
Часть задач есть решенные, контакты
Стационарный режим
Задача 1
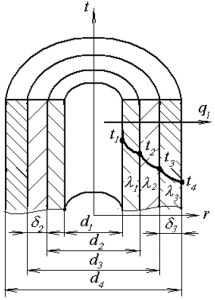
Паропровод диаметром d2/d1 покрыт двухслойной изоляцией (рис. 2.1). Толщина первого слоя изоляции δ2, второго – δ3, мм. Коэффициенты теплопроводности изолируемой трубы и слоев изоляции соответственно равны λ1, λ2, λ3, Вт/(м · К). Температура внутренней и внешней поверхностей паропровода соответственно t1 и t4, °С. Определите тепловые потери одного метра длины трубопровода ql, Вт/м и температуры на поверхностях раздела отдельных слоев t2 и t3, °С. Остальные исходные данные приведены в таблице 2.1.
Стоимость: 150 руб (16 вариант)
Задача 2
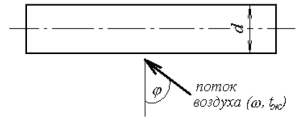
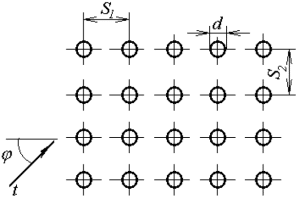
Определите коэффициент теплоотдачи для трубы, омываемой поперечным потоком воздуха (рис. 2.2), если наружный диаметр трубы d, мм, температура воздуха tж, °С, скорость ω (м/с) и угол атаки φ, град имеют значения, приведенные в табл. 2.3, а характеристики сухого воздуха – в таблице 2.2.
Стоимость: 120 руб (16 вариант)
Задача 3
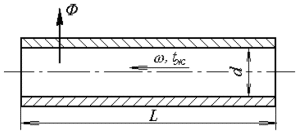
По трубе внутренним диаметром d, мм и длиной L, м протекает вода со скоростью ω, м/с (рис. 2.3). Средняя температура воды – t, °С , а внутренней стенки трубы – tс, °С. Определите коэффициент теплоотдачи от воды к стенке трубы и передаваемый тепловой поток. Исходные данные приведены в таблицах 2.4, 2.5.
Стоимость: 150 руб (16 вариант)
Задача 4
Горизонтальная труба длиной L, м и наружным диаметром d, м расположена в помещении, температура воздуха в котором tв, °С. Средняя температура поверхности трубы tс, °С. Определите величину коэффициента теплоотдачи от трубы к воздуху, а также тепловой поток, теряемый трубой. Исходные данные приведены в таблице 2.6.
Стоимость: 120 руб (16 вариант)
Задача 5
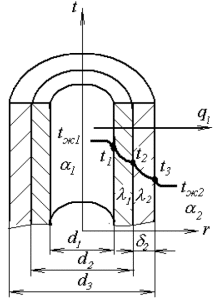
Паропровод диаметром d2/d1 (рис. 2.4) покрыт слоем совелитовой изоляции толщиной δ2, мм. Коэффициенты теплопроводности материала трубы λ1, изоляции λ2 = 0,1 Вт/(м·К). Температуры пара tж1 и окружающего воздуха tж2, °С. Требуется определить линейный коэффициент теплопередачи kl, Вт/(м2 · K), линейную плотность теплового потока ql, Вт/м и температуру наружной поверхности паропровода t3, °С. Исходные данные приведены в таблице 2.7.
Стоимость: 150 руб (16 вариант)
Задача 6
Определите поверхность нагрева стального рекуперативного газовоздушного теплообменника (толщина стенок δс = 3 мм) при прямоточной и противоточной схемах движения теплоносителей (рис. 2.5).
Объемный расход топочных газов при нормальных условиях Vн, м3/ч, средний коэффициент теплоотдачи от воздуха к поверхности нагрева α1, Вт/(м2·К), от поверхности нагрева к воде α2 = 500 Вт/(м2 · К), коэффициент теплопроводности материала стенки трубы (стали) λ = 50 Вт/(м · К), начальные и конечные температуры газа и воды равны соответственно t1н, t1к, t2н и t2к,°С, теплоемкость топочных газов сг = 1,15 кДж/(кг · К), плотность ρг = 1,23 кг/м3. Определите также расход воды G, кг/ч через теплообменник. Изобразите график изменения температур теплоносителей для обеих схем. Исходные данные для расчета приведены в таблице 2.8.
Стоимость: 200 руб (16 вариант)
Задача 7
Электрошина сечением 100 х 10 мм2 и удельным сопротивлением ρ, установленная на ребро, охлаждается свободным потоком воздуха, температура которого tж. При установившейся электрической нагрузке температура электрошины не должна превышать 70°С. Вычислить коэффициент теплоотдачи α, величину теплового потока, теряемого в окружающую среду, если длина электрошины L, и допустимую силу тока. Исходные данные для расчета приведены в таблице 2.9.
Задача 8
Пятирядный коридорный пучок труб диаметром d, мм (расстояние между осями труб по ширине пучка S2 = 60 мм, расстояние между осями двух соседних рядов S1 = 73 мм) омывается поперечным потоком воздуха с температурой tж, °С. Определите среднее значение коэффициента теплоотдачи для пучка αср, Вт/(м2 · К), если скорость движения воздуха в узком сечении ω, м/с и угол атаки потока воздуха φ, град. Исходные данные приведены в таблице 2.10.
Нестационарный режим
Задача 1
Определите температуру в центре tц, °С и на поверхности tп, °С цилиндра диаметром d, м и длиной l, м через 5 часов после помещения его в печь. Начальная температура цилиндра tн, температура внутри печи tж, °С, коэффициент теплопроводности материала цилиндра λ, Вт/(м · К), теплоемкость с, кДж/(кг·К), плотность ρ, кг/м3, коэффициент теплоотдачи α, Вт/(м2 · К). Определите также среднеобъемную температуру цилиндра через 5 часов после начала нагрева и количество теплоты, затраченной на нагрев до температуры tж. Исходные данные для расчета приведены в таблице 2.11, υ0/υ′ и υп/υ′ – на рисунках 1.8, 1.9.
Задача 2
Пластина (брикет) сливочного масла (размером А.В.D мм) охлаждается в холодильной камере, температура воздуха в которой tж, °С. Начальная температура брикета tн, °С. Определите температуру в центре пластины tц, °С через τ мин после начала охлаждения, а также количество теплоты Q (τ), кДж, отводимой от пластины. Коэффициент теплоотдачи принять равным α, Вт/(м2 · K). Теплофизические характеристики материала: λ, Вт/(м · К), a, м2/с, с, кДж/(кг·К). Рассчитайте также среднеобъемную температуру пластины через 5 часов после начала охлаждения. Исходные данные для расчета приведены в таблице 2.12, и Q (τ)/Q – на рисунках 1.7 и 1.10.
Часть задач есть решенные, контакты