Гидравлика Р.173

Р.173

Часть задач есть решенные, контакты

Задача 1

Определить плотность воды и нефти при t = 4 °С, если известно, что (10 + k) л воды при 4 °С имеют массу (10 + k) кг, а масса того же объема нефти равна (8,2 + i) кг. Сравнить плотность нефти с плотностью воды.

Стоимость: 90 руб (i = 4; k = 1)

Задача 2

Цистерна заполнена нефтью плотностью ρ_см = 850 кг/м³. Диаметр цистерны d = (3 + 0,1 i) м, длина l = 6 м. Определить массу жидкости в цистерне.

Задача 3

Плотность нефти при температуре 15^оС равна 828 кг/м³. Условная вязкость ее при температуре (22+k)^oC равна 6,4^оЕ, коэффициент температурного расширения 0,00078К^-1. Определить абсолютную вязкость  нефти при температуре (22+k)^oC.

Стоимость: 120 руб (k = 0)

Задача 4

При испытании прочности баллона он был заполнен водой при давлении (60 + k) кгс/см² через некоторое время в результате утечки части воды через неплотности давление в баллоне снизилось вдвое. Диаметр баллона 350 мм, высота (1200 + 8 k) мм. Определить объем воды, вытекшей при испытании.

Задача 5

Чему равно относительное изменение плотности морской воды (в процентах) при вертикальном погружении на глубину h = 300 м. Плотность морской воды на поверхности ρ₀ = 1030 кг/м³.

Стоимость: 90 руб 

Задача 6

Баллон, вместимость которого равна (36 + 2k) дм³ заполнен нефтью и плотно закрыт при давлении 0,1 МПа. Какое количество нефти необходимо закачать в баллон дополнительно, чтобы давление в нем повысилось в 25 раз?

Стоимость: 90 руб (k = 2)

Задача 7

23,5 тонн бензина при температуре 3 °С занимают объем (33,25 + 0,1k) м³. Какой объем будет занимать это же количество бензина при температуре 17 °С, если давление не изменится? Коэффициент температурного расширения бензина 0,00065 К^-1.

Стоимость: 90 руб (k = 0; k = 1)

Задача 8

При испытании прочности резервуара он был заполнен водой при давлении (50 – 0,2 i) атм. Через некоторое время в результате утечки части воды через неплотности давление понизилось до (11,5 + 0,2 i) ат. Определить объем воды, вытекшей за время испытания. Вместимость резервуара равна 20 м³.

Задача 9

Бензин весом (43,5 – 0,2i) тонны при температуре 15 °С занимает объем 33,5 м³. Какой объем будет занимать это же количество бензина при температуре 6 °С? Коэффициент температурного расширения бензина 0,00065 град^-1.

Стоимость: 90 руб (i = 2)

Задача 10

В резервуар закачено (15 – 0,2i) м³ нефти удельного веса 800 кгс/м³ и (16 – 0,2i) м³ нефти неизвестного удельного веса. Удельный вес смеси стал равным 824 кгс/м³. Определить удельный вес долитой нефти.

Стоимость: 120 руб (i = 2)

Задача 11

Для испытания резервуара на прочность он заполнен водой под давлением 50 атм. Вследствие утечки воды давление в резервуаре понизилось до (42 – 0,1 k) атм. Сколько воды вытекло из резервуара, если он имеет форму цилиндра с диаметром 500 см и высотой 800 см?

Стоимость: 120 руб (k = 11)

Задача 12

Определить, насколько поднимется уровень нефти в цилиндрическом резервуаре при увеличении температуре от 15 до 40ºС. Плотность нефти при 15ºС ρ₁₅ = 900 кг/м³. Диаметр резервуара d = 10 м; нефть заполняет резервуар при 15ºС до высоты Н = (12 – 0,1 k) м. Коэффициент теплового объемного расширения нефти β_т = 6,4 – 10^-4 1/градус. Расширение резервуара не учитывается.

Задача 13

Вода поступает в насос по всасывающей трубе, работающей под вакуумом. Минимальное абсолютное давление перед входом в насос p = 4 кПа. Температура перекачиваемой воды поднялась до 30 °С. Будет ли в этом случае наблюдаться кипение и кавитация?

Стоимость: 90 руб 

Задача 14

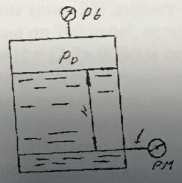
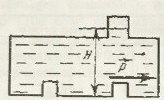
В закрытом резервуаре (рис. 21) с нефтью плотностью ρ = 880 кг/м³ вакуумметр, установленный на его крышке, показывает р_в = (1,18 + 0,2k) · 10⁴ Па. Определить показание манометра р_м, присоединенного к резервуару на глубине H = 6 м от поверхности жидкости, и положение пьезометрической плоскости.

Стоимость: 120 руб (k = 1)

Задача 15

Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двухжидкостного ртутного манометра (рис. 22): h₁ = (82 – 0,1 k) см; h₂ = (39 – 0,2 i) см; h₃ = 54 см; h₄ = (41 + 0,2 k) см; h₅ = 100 см; ρ = 10³ кг/м³; ρ_р = 1,36 · 10⁴ кг/м³.

Задача 16

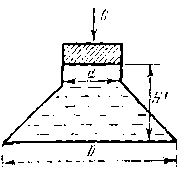
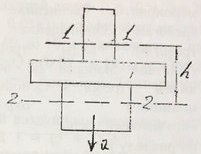
Найти силу давления воды на дно сосуда диаметром D = (1 + 0,2k) м (рис. 23), если глубина H‘ = (0,7 + 0,2k) м, вес поршня G = 300 Н, d = 0,5 м.

Стоимость: 90 руб (k = 0; k = 1)

Задача 17

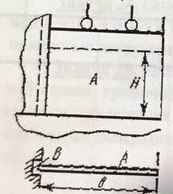
Вертикальный щит А (рис. 24), перекрывающий водослив, может перемещаться в пазах В вверх и вниз. Глубина жидкости H = (1,4 + 0,2i) м, ширина щита b = (2,6 + 0,2k) м. Какую силу нужно приложить, чтобы поднять щит, если его вес G = (32 + 0,1i) кН, а коэффициент трения между щитом и поверхностью пазов f = 0,3.

Стоимость: 90 руб (i = 2; k = 2)

Задача 18

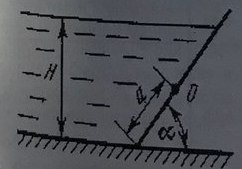
Наклонный прямоугольный щит плотины шарнирно закреплен на оси О (рис. 26). При каком уровне воды Н щит опрокинется, если угол наклона щита α = (60 + 0,9 i)º, а расстояние от его нижней кромки до оси шарнира а = (1,3 + 0,21) м. Вес щита не учитывать.

Задача 19

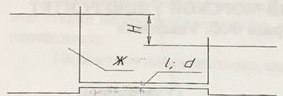
Определите силу давления жидкости на торцевую плоскую стенку горизонтальной цилиндрической цистерны (рис. 27) диаметром d = (2,4 + 0,2k) м, заполненной бензином плотностью ρ = 760 кг/м³, если уровень бензина в горловине находится на расстоянии H = (2,7 + 0,2k) м от дна. Цистерна герметично закрыта и избыточное давление на поверхности жидкости составляет (40 + 0,2i) кПа. Найти также положение центра давления относительно центра тяжести стенки.

Стоимость: 120 руб (i = 3; k = 2)

Задача 20

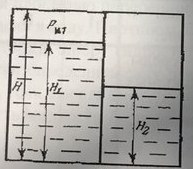
Закрытый резервуар высотой Н = (10 – 0,1 i) м (рис. 25) разделен на два отсека вертикальной прямоугольной перегородкой шириной b = 4 м. В левом отсеке уровень нефти Н₂ = (8 – 0,1 k) м (ρ_н = 850 кг/м³), в правом уровень воды Н₁ = (5 – 0,1 k) м (ρ_в = 1000 кг/м³). Избыточное давление паров над нефтью ρ_i1 = 19,6 кПа. Определить равнодействующую сил давления на перегородку и точку ее приложения. Указание. В левом отсеке, кроме силы давления нефти и паров, на смоченную часть перегородки, нужно учесть силу давления паров на не смоченную часть стенки.

Задача 21

Шаровой резервуар диаметром d = (1 + 0,2 k) целиком заполнен жидкостью ρ = 10³ кг/м³. В верхней точке жидкости в резервуаре давление атмосферное. Определить величины и направления сил, действующих на верхнюю и боковую полусферы.

Стоимость: 250 руб (k = 5)

Задача 22

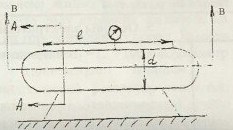
Горизонтальная цилиндрическая цистерна с полусферическим днищами целиком заполнена топливом ρ = 800 кг/м³. Давление в верхней части цистерны, измеряемое манометром, р_м = (14,7 + 0,2 k) кПа, длина цистерны l = 5 м, ее диаметр d = 3 м (рис. 28). Определить величины сил давления, растягивающих цистерну в сечениях А – А и В – В, и положение линий их действия.

Задача 23

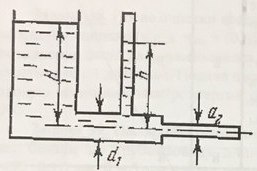
Из напорного бака вода течет по трубе диаметром d₁ = (20 + 0,2 k) мм и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d₂ = 10 мм. Избыточное давление в баке Р₀ = (0,18 + 0,1 k) МПа. Пренебрегая потерями, определить скорость течения воды в трубе ₁ и на выходе из насадка . Высота жидкости над осью трубы Н = 1,6 м (рис. 29).

Задача 24

Определить силу, действующую на деревянный брус длиной L = (0,5 + 0,3 k) м и площадью поперечного сечения F = (0,02 + 0,2 k) м², полностью погруженный в воду. Плотность бруса принять ρ_б = 600 кг/м³.

Задача 25

Построить эпюру гидростатического давления для плоской стенки, графически определить силу давления жидкости на стенку и место ее приложения, если высота смоченной поверхности h, давление на свободную поверхность жидкости p₀, ширина стенки b, плотность жидкости ρ_ж.

Стоимость: 120 руб 

 Задача 26

Открытая емкость в виде усеченного конуса стоит на меньшем основании и полностью заполнена жидкостью с плотностью ρ = 1100 кг/м³. Определить результирующую силу давления жидкости на дно емкости и силу давления емкости на горизонтальную опору. Высота емкости h = (2 + 0,2k) м, диаметр нижнего сечения d₁ = (2 + 0,2k) м, диаметр верхнего сечения d₂ = 3 м.

Стоимость: 90 руб (k = 0)

Задача 27

Вертикальный цилиндрический резервуар емкостью W = (1000 + 20 k) м³, высотой Н = 13 м заполнен нефтью с плотностью ρ_н = 880 кг/м³. Определить силы давления нефти на боковую стенку и дно резервуара.

Задача 28

Какой объем бензина (ρ = 740 кг/м³) можно залить в железнодорожную цистерну внутренним объемом (50 + 0,2 k) м³ и массой (23 + 0,2 i) т, чтобы она еще сохраняла плавучесть в пресной воде?

Задача 29

Из открытого резервуара с постоянным уровнем (рис. 30) идеальная жидкость по горизонтальной трубе вытекает в атмосферу, H = (1,6 + 0,1k) м; d₁ = 0,15; d₂ = 0,075 м. Определить уровень жидкости в пьезометре h.

Стоимость: 120 руб (k = 0)

Задача 30

Поток воды у входа в турбину (рис. 31) в сечении 1 – 1 имеет скорость υ₁ = (3 + 0,2 i) м/с и давление р₁ = 2 МПа. На выходе из турбины сечения 2 – 2 υ₂ = (1,2 + 0,1 k) м/с, р₂ = 0,05 МПа. Расход воды через турбину Q = (9 + 0,2 k) · 10³ м³/ч. Расстояние между сечениями h = 0,5 м. Определить мощность N на валу турбины, если к.п.д. турбины η = 0,85.

Задача 31

По трубопроводу перекачивается нефть плотностью ρ = 910 кг/м³ в количестве Q = (0,04 + 0,1k) м³/c (рис. 31). Сечение 2–2 расположено выше сечения 1–1 на 10 м. Диаметры трубы d₁ = (0,3 + 0,1k) м; d₂ = 0,2 м; давления p₁ = 1,5 МПа, p₂ = 1 МПа. Определить потерю напора h_п1-2.

Стоимость: 120 руб (k = 0; k = 2)

Задача 32

По горизонтальной трубе течет жидкость плотностью ρ = 10³ кг/м³, расход Q = 2,5 · 10^-3 м³/с, диаметр D = 0,05 м. Определить, пренебрегая потерями напора, диаметр d, если разность давлений р₁ – р₂ = 15 кПа.

Стоимость: 120 руб 

Задача 33

По трубе d = (0,1 + 0,1 k) м течет вода. Определить максимальные скорость течения υ и расход Q, при которых режим течения будет оставаться ламинарным. Вязкость воды μ = 10^-3 кг/м · с.

Задача 34

При течении нефти в трубопроводе диаметром d = (0,2 + 0,1k) м массовый расход Q_м = (35 + 11k) т/ч. Нефть заполняет сечение трубопровода до высоты h = d/2. Динамическая вязкость нефти μ = 0,12 кг/м · с. Определить режим течения.

Стоимость: 120 руб (k = 3)

Задача 35

Известен перепад давления на сборном коллекторе Δр = 3 МПа, расход нефти Q = (400 + 5k) т/сут, разность высот отметок конца и начала коллектора Δz = 20 м, длина его (4 + 0,1k) км, плотность нефти ρ = 0,8 т/м³, вязкость ν = 20 мм²/с. Необходимо определить диаметр коллектора.

Стоимость: 120 руб (k = 0)

Задача 36

В начало сборного коллектора длиной L = 10 км, диаметром (0,2 + 0,1 k) м подают товарную нефть в количестве Q = Q_т = Q_п = 180 т/ч, вязкостью η = 20 мПа · с и ρ = 800 кг/м³, из сбороного коллектора нефть отбирают в трех точках соответственно с q₁ = 20 т/ч, q₂ = 50 т/ч, q₃ = 100 т/ч. Расстояние от начала коллектора и до точек отбора нефти следующие: L₁ = 4 км, L₂ = 200 м, L₃ = 3 км. Определить общий перепад давления, если начальное давление равно (1,6 + 0,5 k) Мпа. Сборный коллектор проложен горизонтально и местных сопротивлений не имеет.

Задача 37

Определить относительное изменение потерь напора при Q = Idem на участке А-В = (5 + 0,1k) км (d₁ = 200 мм), если к нему подключить лупинг той же длины (d₂ = 260 мм). Лупингом называется труба, подключаемая к участку трубопровода для уменьшения его гидравлического сопротивления. Трубы сварные новые, местными сопротивлениями пренебречь.

Стоимость: 180 руб (k = 0; k = 1)

Задача 38

После очистки всасывающей линии (l = 10 м, d = 200 мм) насосной установки (к.п.д. η_нас = (0,65 + 0,01 k)) коэффициент местного сопротивления фильтра ζ_ф уменьшился с 40 до 10, а эквивалентная шероховатость труб с 1 до 0,1 мм. Подача насоса Q (0,07 + 0,1 k) м³/с. Определить годовую экономию электроэнергии от этой операции. Температура воды 20ºС.

Задача 39

Насос, оборудованный воздушным колпаком, перекачивает бензин по трубопроводу длиной l = (5 + 0,1k) км, диаметром d = (75 + 0,1i) мм, δ = 5 мм в количестве Q = 9 · 10^-3 м³/с. Плотность бензина ρ = 740 кг/м³, модуль упругости бензина K = 1,1 · 10⁹ Па, Е = 2 · 10¹¹ Па. Определить, за какое время необходимо перекрыть задвижку, чтобы ударное повышение давления не превосходило 1 МПа.

Стоимость: 90 руб (i = 4; k = 1)

Задача 40

По трубопроводу длиной l_пр = (20 + 0,1 i) м, диаметром d = (0,5 + 0,1 k) м, δ = 3,5 мм, соединенному с баком, под напором Н = 2,5 м течет вода (К = 2 · 10⁹ Па). В некоторый момент времени происходит мгновенное перекрытие потока в конце трубопровода. Найти скорость распространения волны гидравлического удара и величину ударного повышения давления, если труба стальная (Е = 2 · 10¹¹ Па). Коэффициент гидравлического сопротивления принять равным 0,03. Как изменится ударное повышение давления, если стальную трубу заменить чугунной тех же размеров (Е = 0,98 · 10¹¹ Па)?

Задача 41

Вода (t = 20 ⁰С) перетекает из резервуара А в резервуар В, давления на поверхности жидкости в которых одинаковы (рис. 33). Соединительный трубопровод состоит из двух последовательно соединенных участков новых стальных бесшовных труб (l₁ = (200 + 5k) м, d₁ = 100 мм и l₂ = (150 + 3k) м, d₂ = 80 мм), для обеих труб эквивалентная длина местных сопротивлений l_экв = 0,05l, h = 3 м. Определить расход воды.

Стоимость: 250 руб (k = 0; k = 1; k = 2)

Задача 42

По приведенному на рис. 34 сифонному сливу (l = 50 м, d = (100 + 10 k) мм, Δ = 0,06 мм) подается топливо (ρ = 840 кг/м³, ν = 5,5 · 10^-6 м²/с) при разности отметок уровней в резервуарах Н₁ = 1,38 м. На сливе имеются фильтр для светлых нефтепродуктов, два колена и вентиль; Н₂ = (3 + 0,1 k) м, Н₃ = 2 м, давление насыщенных паров при температуре перекачки р_п = 2 кПа, р_а = 105 Па. Определить расход жидкости и проверить условие нормальной работы сифона.

Стоимость: 300 руб (k = 11)

Задача 44

Определить время опорожнения вертикального цилиндрического резервуара D = (8 + 0,5k) м, заполненного нефтью до уровня H = (10 + k) м. Истечение осуществляется через цилиндрический внешний насадок (d = 5 см и длина l = 20 см). Кинематическая вязкость нефти ν = 120 мм²/с, плотность ρ = 880 кг/м³.

Стоимость: 150 руб (k = 2)

Задача 47

По трубопроводу диаметром d = (30 + k) мм и длиной l = (5 + 0,1k) м движется вода (рис. 37). Чему равен напор H, при котором происходит смена ламинарного режима турбулентным? Местные потери напора не учитывать. Температура жидкости t = 20 °С.

Стоимость: 120 руб (k = 0)

Задача 49

Из цилиндрического вертикального резервуара – отстойника D = (3,5 + 0,1i) м, предназначенного для разделения нефти и загрязненной воды, через донную вертикальную трубу (L = (0,5 + 0,1i) м, d = 0,125 м) сливается вода (ρ_в = 1100 кг/м³, ν = 1 мм²/с). Начальный уровень воды в резервуаре h_в = 4 м, нефти h_н = 1 м. Необходимо определить время слива воды, считая, что имеется четкая граница раздела воды и нефти (ρ_н = 880 кг/м³).

Стоимость: 180 руб (i = 2, 3; k = 2)

Задача 50

Определить предельную высоту установки насоса над поверхностью воды в приемном резервуаре. Насос перекачивает воду с температурой t = 30 °C в количестве Q = 50 л/с. Длина всасывающего трубопровода l_вс = 55 м, его диаметр d_вс = 200 мм, коэффициент потерь по длине трубы λ = 0,035. На всасывающем трубопроводе имеются местные сопротивления, сетка (фильтр на всасывании), колено и задвижка. Значения коэффициентов местных сопротивлений ζ_сет = 8,0, ζ_кол = 0,3, ζ_зад = 4,0.

Стоимость: 120 руб 

Часть задач есть решенные, контакты