Гидравлика и водоснабжение ДВГУПС

РХ.ДВГУПС.5

Решение задач по гидравлике

Есть готовые решения этих задач, контакты

Задача 1.3.1

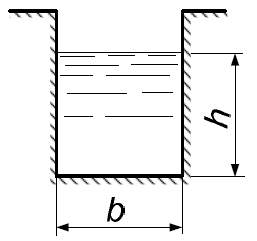
Определить гидравлический радиус потока в канале прямоугольного сечения (см. рис. 1.3), шириной b, если глубина потока h.

Стоимость: 90 руб (Вариант 3, 4)

Задача 1.3.2

Определить гидравлический радиус речного потока (рис. 1.4),  если ширина потока B, а средняя глубина потока h_ср. При расчете сечение потока принимается прямоугольным, размерами B×h_ср.

Стоимость: 90 руб (Вариант 1)

Задача 1.3.3

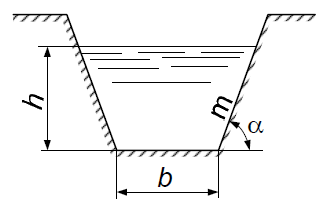
Определить гидравлический радиус потока в открытом канале трапецеидального сечения (рис. 1.5), если глубина потока h, ширина канала по дну b, коэффициент заложения откоса m = ctgα.

Стоимость: 90 руб (Вариант 3, 4, 5)

Задача 1.3.4

В горизонтальном полочном отстойнике (рис. 1.6) устанавливается пакет пластин, который служит для успокоения потока и для улучшения процесса очистки воды. Вертикальное расстояние между пластинами h, глубина проточной части отстойника H, его ширина b. Определить гидравлические радиусы потока: R₁ – в сечении I — I перед пакетом пластин и R₂ – в сечении II — II, т. е. на участке, где установлен пакет. Толщиной пластин пренебречь.

Задача 1.3.7

Определить среднюю скорость воды V в вертикальном отстойнике (рис. 1.8) диаметром D, если расход обрабатываемой воды Q. При расчете пренебречь площадью, занимаемой центральной трубой для подачи воды в отстойник.

Стоимость: 90 руб (Вариант 1)

Задача 1.3.9

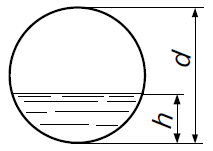
Наибольшее расчетное наполнение канализационных труб h/d. Определить соответствующий расход воды, если диаметр трубы d, а допустимая скорость равна V. Площадь живого сечения труб в зависимости от наполнения принимать по прил. 1.

Стоимость: 90 руб (Вариант 1, 3, 5)

Задача 2.3.1

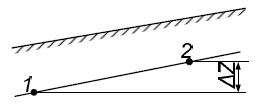
Определить напор, который должен поддерживаться в точке 1 водослива постоянного сечения (рис. 2.8) для подачи воды с расходом Q. Геодезические отметки точек 1 и 2, соответственно, Z₁ = 0,00 и Z₂, свободный напор в точке 2 H_св. Потери напора определяются по формуле (2.7).

Стоимость: 120 руб (Вариант 1, 3, 4, 5)

Задача 2.3.3

Определить манометрическое давление Р в баке 1 гидропневматической установки (рис. 2.10), если вода подается по трубопроводу к водозабору 2, расположенному выше дна бака на ΔZ. Свободный напор перед водозабором равен Н_св = 12 м, расход воды в трубопроводе Q, а потери напора на участке 1 – 2 определяются по формуле (2.7). При решении толщиной воды в баке 1 и изменением скоростного напора пренебречь.

Стоимость: 90 руб (Вариант 1, 3, 6)

Задача 2.3.4

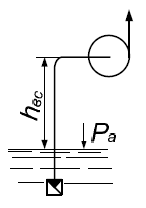
Определить максимальную высоту всасывающего насоса h_вс (рис. 2.11), если при подаче расхода Q он создает вакуум p_вак = 86 кПа. Удельный вес перекачиваемой жидкости γ, потери напора во всасывающей линии определяются по формуле h_w = 1,2S · Q², где S = 10³ с²/м⁵. При решении изменением скоростного напора пренебречь.

Стоимость: 120 руб (Вариант 2)

Задача 2.3.7

Определить максимально допустимые потери напора h_w в водоводе (рис. 2.14), если его конечная точка 2 выше начальной 1 на величину ΔZ, а свободный напор в конечной точке должен быть не менее Н_св. Давление воды в начальной точке равно p₁. Скоростным напором при решении задачи пренебречь.

Стоимость: 90 руб (Вариант 5)

Задача 2.3.12

На рис. 2.17 показан профиль водовода, в начальной точке которого поддерживается напор H (относительно оси трубы с отметкой Z₁ = 0,00). Построить пьезометрическую линию и определить гидравлический уклон, постоянный для всего водовода, при условии, что давление в водоводе не падает ниже p_ман = 0,1 МПа.

Стоимость: 120 руб (Вариант 4)

Задача 2.3.14

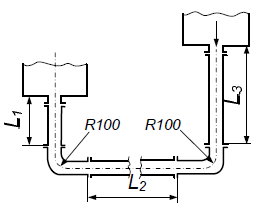
Построить пьезометрическую линию для сифона, продольный профиль которого показан на рис. 2.19. Уровни воды в верховом и низовом колодцах Z_в = +10,0 и Z_н; гидравлический уклон на всех участках сифона одинаков, в точках 1 и 4 местные потери напора равны потерям напора на участке длиной по 10 м, в точках 2 и 3 – на участке длиной 5 м. Укажите участки, на которых имеется вакуум.

Стоимость: 150 руб (Вариант 3, 6)

Задача 2.3.15

Построить пьезометрическую линию и определить, в каких интервалах может изменяться давление в начале водовода (рис. 2.20) с отметкой оси трубы Z₁ = 0,00, если гидравлический уклон при максимальном расходе воды равен I₁, а при минимальном I₂. Давление в пределах водовода не должно превышать значения p_мак = 1,6 МПа и быть ниже p_мин = 0,1 МПа. Значения гидравлического уклона I для всего водовода одинаково.

Стоимость: 180 руб (Вариант 2)

Задача 3.3.1

Определить число Рейнольдса и режим движения для потока жидкости, проходящего в трубе с расходом Q. Внутренний диаметр трубы d, кинематический коэффициент вязкости жидкости ν. Критическое значение числа Рейнольдса 2000.

Стоимость: 60 руб (Вариант 1, 3, 4, 5)

Задача 3.3.3

Определить число Рейнольдса Re₁ и Re₂ в сечениях I — I и II — II при работе полочного отстойника, схема и габариты которого для соответствующих вариантов указаны в задаче 1.3.4. Дополнительные данные: производительность отстойника Q, кинематический коэффициент вязкости – 0,014 см²/с.

Стоимость: 120 руб (Вариант 3, 6)

Задача 3.3.5

Нефтеловушка представляет собой прямоугольный проточный резервуар шириной b. Определить максимальную производительность нефтеловушки Q, если глубина воды в ней h, кинематический коэффициент вязкости воды 0,014 см²/с, а максимальное значение числа Рейнольдса, обеспечивающее хорошую работу сооружения и определяющееся по эмпирической формуле, равно Re_доп.

Стоимость: 90 руб (Вариант 2)

Задача 3.3.7

Трубопровод диаметром d плавно расширяется, режим движения жидкости турбулентный при Re. Определить диаметр D в широком сечении трубопровода, при котором движение будет ламинарным.

Стоимость: 120 руб (Вариант 1)

Задача 3.3.8

По трубопроводу диаметром d движется вода с кинематическим коэффициентом вязкости 0,0114 см²/с. Расходы воды определяются при помощи мерного сосуда и секундомера. Определить время наполнения сосуда емкостью W при режимах движения воды, соответствующих верхнему и нижнему критическому числу Рейнольдса.

Стоимость: 90 руб (Вариант 1, 3)

Задача 4.3.2

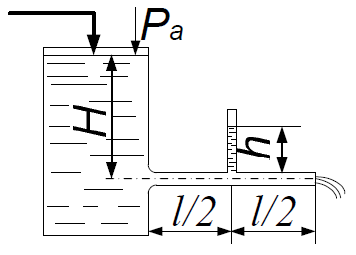
При истечении воды из резервуара в атмосферу по горизонтальной трубе диаметром d и длиной l статический напор равен H, а уровень воды в пьезометре, установленном в середине трубы, h. Определить коэффициент сопротивления трения λ трубы. Сопротивлением входа в трубу пренебречь.

Стоимость: 150 руб (Вариант 1, 3, 4)

Задача 4.3.3

Определить превышение оси трубопровода 1 (рис. 4.5) над центром сливного отверстия h, если расход масла в трубопроводе Q, давление на выходе из резервуара P_м, длина трубопровода l, диаметр d, кинематический коэффициент вязкости 0,14 см²/с, а плотность масла 860 кг/см². Местными сопротивлениями пренебречь.

Стоимость: 150 руб (Вариант 3, 6)

Задача 4.3.4

Определить потери напора при движении воды со скоростью V по трубе диаметром d и длиной l. Трубы стальные новые, кинематический коэффициент вязкости 0,0131 см²/с.

Стоимость: 90 руб (Вариант 1, 2, 3)

Задача 4.3.8

Определить общие потери напора h в трубопроводе диаметром d = 50 мм, соединяющим два резервуара (рис. 4.9), если по нему течет вода со скоростью V. Кинематический коэффициент вязкости 0,01 см²/с. При решении использовать формулу Блазиуса по прил. 4.

Стоимость: 120 руб (Вариант 1)

Задача 4.3.12

По формуле Альтшуля определить коэффициент сопротивления λ для трубы диаметром d = 300 мм. Расход воды, проходящей по трубе, Q, кинематический коэффициент вязкости 0,012 см²/с, эквивалентная шероховатость внутренней поверхности трубы Δ_э = 1,2 мм.

Стоимость: 60 руб (Вариант 5)

Задача 5.3.1

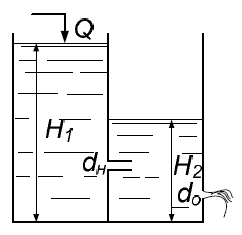
В бак, разделенный перегородкой на два отсека (рис. 5.6), подается вода в количестве Q при кинематическом коэффициенте вязкости 0,0101 см²/с. В перегородке имеется цилиндрический насадок, диаметр которого d_н. Жидкость из второго отсека через отверстие диаметром d_о вытекает в атмосферу. Определить уровни жидкости в обоих отсеках H₁ и H₂.

Стоимость: 120 руб (Вариант 4)

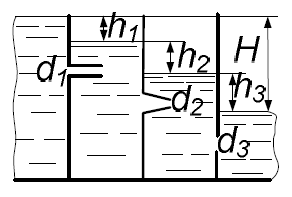
Задача 5.3.3

Резервуар (рис. 5.8) состоит из трех сообщающихся между собой камер. Определить расход воды и уровни в каждой камере. Диаметр цилиндрического насадка в первой перегородке d₁, диаметр конического насадка во второй перегородке d₂, диаметр отверстия в третьей перегородке d₃. Общий перепад уровней Н. Кинематический коэффициент вязкости равен 0,0101 см²/с.

Стоимость: 150 руб (Вариант 3, 6)

Задача 5.3.5

Вода вытекает из сосуда через малое отверстие в тонкой стенке диаметром d под напором Н. Определить массовый расход воды G и диаметр струи d_с, приняв коэффициент кинематической вязкости 0,01 см²/с. При решении использовать графическую зависимость, представленную на рис. 5.2.

Стоимость: 120 руб (Вариант 2)

Задача 5.3.7

Вода вытекает из открытого бака через цилиндрический насадок диаметром d при постоянном напоре H. Сосуд емкостью 20 л, подставленный под струю, заполнился за время t. Определить потери напора h_м в насадке.

Стоимость: 120 руб (Вариант 1, 5)

Задача 5.3.11

Определить диаметр d внешней цилиндрической насадки, необходимой для опорожнения вертикального цилиндрического резервуара (рис. 5.13) для воды в течение времени t. Диаметр резервуара D, максимальный уровень воды на h выше насадка. Коэффициент расхода насадка μ = 0,62 (с учетом сопротивления вентиля).

Стоимость: 120 руб (Вариант 1, 3)

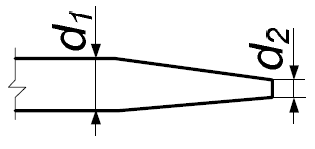
 Задача 5.3.15

Определить силу, действующую на пожарный ствол, присоединенный к напорному рукаву диаметром d₁, диаметр спрыска d₂ (рис. 5.17), расчетный расход струи Q. Коэффициент расхода спрыска μ = 0,97.

Стоимость: 120 руб (Вариант 1, 3)

Есть готовые решения этих задач, контакты